 1.旅行商问题
1.旅行商问题
旅行商问题(Traveling Salesman Problem,TSP),是由爱尔兰数学家Sir William Rowan Hamilton和英国数学家Thomas Penyngton Kirkman在19世纪提出的数学问题。它的描述是这样的:一名商人要到若干城市去推销商品,已知城市个数和各城市间的路程(或旅费),要求找到一条从城市1出发,经过所有城市且每个城市只能访问一次,最后回到城市1的路线,使总的路程(或旅费)最小。现已证明它属于NP(Non-deterministic Polynomial---非确定多项式)难题。
若设城市数目为n时,那么组合路径数则为(n-1)!。当城市数量较小时,通过枚举法就可以找出最短的路径。随着城市数目的不断增大,组合路线数将呈指数级数规律急剧增长,以至达到无法计算的地步。此时,很难找到一个多项式时间复杂度的算法来求解该问题。
TSP是一个典型的组合优化问题,是诸多领域内出现的多种复杂问题的集中概括和简化形式,并且已成为各种启发式的搜索、优化算法的间接比较标准。
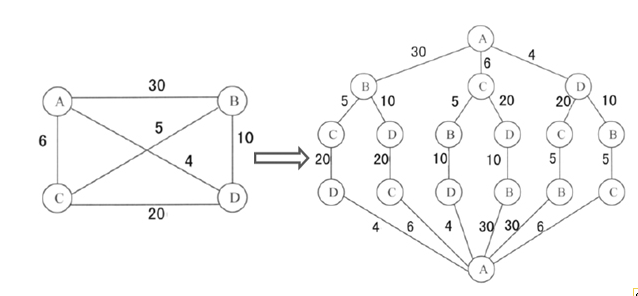
图1 当城市数量较少时,直接通过枚举求解
2.模拟退火法
2.1算法
模拟退火算法由KirkPatrick于1982提出,他将退火思想引入到组合优化领域,提出一种求解大规模组合优化问题的方法,对于NP-完全组合优化问题尤其有效。(化学上的退火方法讲述比较复杂,有兴趣的可以自行查找)
模拟退火算法可以分解为解空间、目标函数和初始解3部分。其基本思想是:
(1)初始化:初始温度T(充分大),初始解状态s(是算法迭代的起点),每个T值的迭代次数L;
(2)对k=1,……,L做第(3)至第6步;
(3)产生新解s′;
(4)计算增量cost=cost(s′)-cost(s),其中cost(s)为评价函数;
(5)若t<0则接受s′作为新的当前解,否则以概率exp(-t′/T)接受s′作为新的当前解;
(6)如果满足终止条件则输出当前解作为最优解,结束程序。终止条件通常取为连续若干个新解都没有被接受时终止算法;
(7)T逐渐减少,且T趋于0,然后转第2步运算。
2.2 参数选择
(1)温度T的初始值设置。
温度T的初始值设置是影响模拟退火算法全局搜索性能的重要因素之一。初始温度高,则搜索到全局最优解的可能性大,但因此要花费大量的计算时间;反之,则可节约计算时间,但全局搜索性能可能受到影响。实际应用过程中,初始温度一般需要依据实验结果进行若干次调整。
(2)温度衰减函数的选取。
衰减函数用于控制温度的退火速度,一个常用的函数为:
T(t+1)=aT(t)
式中a是一个非常接近于1的常数,t为降温的次数。
(3)马尔可夫链长度L的选取。
通常的原则是:在衰减参数T的衰减函数已选定的前提下,L的选取应遵循在控制参数的每一取值上都能恢复准平衡的原则。
3. TSP算法实现
3.1 TSP算法描述
(1)TSP问题的解空间和初始解
TSP的解空间S是遍访每个城市恰好一次的所有回路,是所有城市排列的集合。TSP问题的解空间S可表示为{1,2,…,n}的所有排列的集合,即S = {(c1,c2,…,cn) | ((c1,c2,…,cn)为{1,2,…,n}的排列)},其中每一个排列Si表示遍访n个城市的一个路径,ci= j表示在第i次访问城市j。模拟退火算法的最优解与初始状态无关,故初始解为随机函数生成一个{1,2,…,n}的随机排列作为S0。
(2)目标函数
TSP问题的目标函数即为访问所有城市的路径总长度,也可称为代价函数:

现在TSP问题的求解就是通过模拟退火算法求出目标函数C(c1,c2,…,cn)的最小值,相应地,s*= (c*1,c*2,…,c*n)即为TSP问题的最优解。
(3)新解产生
新解的产生对问题的求解非常重要。新解可通过分别或者交替用以下2种方法产生:
①二变换法:任选序号u,v(设uvn),交换u和v之间的访问顺序,若交换前的解为si= (c1,c2,…,cu,…,cv,…,cn),交换后的路径为新路径,即:
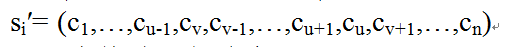
②三变换法:任选序号u,v和ω(u≤vω),将u和v之间的路径插到ω之后访问,若交换前的解为si= (c1,c2,…,cu,…,cv,…,cω,…,cn),交换后的路径为的新路径为:
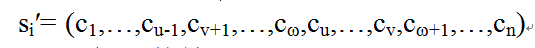
(4)目标函数差
计算变换前的解和变换后目标函数的差值:
![]()
(5)Metropolis接受准则
根据目标函数的差值和概率exp(-ΔC′/T)接受si′作为新的当前解si,接受准则:
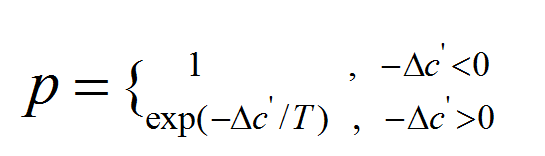
3.2 TSP算法流程
根据以上对TSP的算法描述,可以写出用模拟退火算法解TSP问题的流程图2 所示:
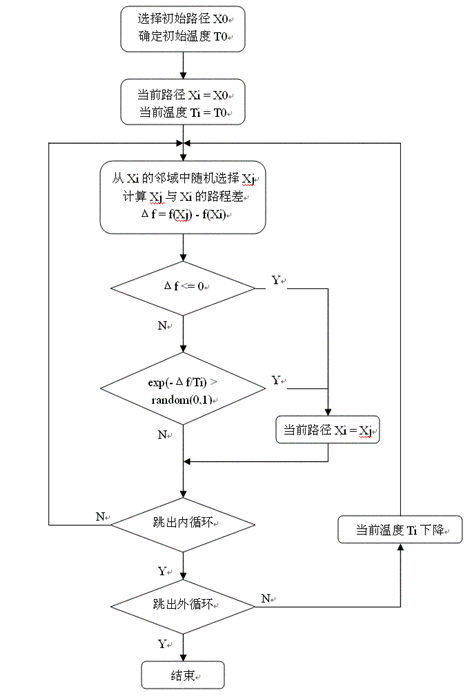
图 2 TSP的模拟退火流程
4.MATLAB实现
clear
clc
coordinates = load('data.txt'); %加载数据
%设置参数
a = 0.99; % 温度衰减函数的参数
t0 = 97; tf = 3; t = t0;
Markov_length = 10000; % Markov链长度
amount = size(coordinates,1); % 城市的数目
% 通过向量化的方法计算距离矩阵
dist_matrix = zeros(amount, amount);
coor_x_tmp1 = coordinates(:,1) * ones(1,amount);
coor_x_tmp2 = coor_x_tmp1';
coor_y_tmp1 = coordinates(:,2) * ones(1,amount);
coor_y_tmp2 = coor_y_tmp1';
dist_matrix = sqrt((coor_x_tmp1-coor_x_tmp2).^2 + (coor_y_tmp1-coor_y_tmp2).^2); %存储各个城市之间距离的矩阵
sol_new = 1:amount; % 产生初始解
% sol_new是每次产生的新解;sol_current是当前解;sol_best是冷却中的最好解;
E_current = inf;E_best = inf; % E_current是当前解对应的回路距离;
% E_new是新解的回路距离;
% E_best是最优解的
sol_current = sol_new; sol_best = sol_new;
p = 1;
while t>=tf
for r=1:Markov_length % Markov链长度
% 产生随机扰动
if (rand < 0.5) % 随机决定是进行两交换还是三交换
% 两交换
ind1 = 0; ind2 = 0;
while (ind1 == ind2)
ind1 = ceil(rand.*amount);
ind2 = ceil(rand.*amount);
end
tmp1 = sol_new(ind1);
sol_new(ind1) = sol_new(ind2);
sol_new(ind2) = tmp1;
else
% 三交换
ind1 = 0; ind2 = 0; ind3 = 0;
while (ind1 == ind2) || (ind1 == ind3)|| (ind2 == ind3) || (abs(ind1-ind2) == 1)
ind1 = ceil(rand.*amount);
ind2 = ceil(rand.*amount);
ind3 = ceil(rand.*amount);
end
tmp1 = ind1;tmp2 = ind2;tmp3 = ind3;
% 确保ind1 < ind2 < ind3
if (ind1 < ind2) && (ind2 < ind3)
;
elseif (ind1 < ind3) && (ind3 < ind2)
ind2 = tmp3;ind3 = tmp2;
elseif (ind2 < ind1) && (ind1 < ind3)
ind1 = tmp2;ind2 = tmp1;
elseif (ind2 < ind3) && (ind3 < ind1)
ind1 = tmp2;ind2 = tmp3; ind3 = tmp1;
elseif (ind3 < ind1) && (ind1 < ind2)
ind1 = tmp3;ind2 = tmp1; ind3 = tmp2;
elseif (ind3 < ind2) && (ind2 < ind1)
ind1 = tmp3;ind2 = tmp2; ind3 = tmp1;
end
tmplist1 = sol_new((ind1+1):(ind2-1));
sol_new((ind1+1):(ind1+ind3-ind2+1)) = sol_new((ind2):(ind3));
sol_new((ind1+ind3-ind2+2):ind3) = tmplist1;
end
%检查是否满足约束
% 计算目标函数值(即内能)
E_new = 0;
for i = 1 : (amount-1)
E_new = E_new + dist_matrix(sol_new(i),sol_new(i+1));
end
% 再算上从最后一个城市到第一个城市的距离
E_new = E_new + dist_matrix(sol_new(amount),sol_new(1));
if E_new < E_current
E_current = E_new;
sol_current = sol_new;
if E_new < E_best
% 把冷却过程中最好的解保存下来
E_best = E_new;
sol_best = sol_new;
end
else
% 若新解的目标函数值小于当前解的,
% 则仅以一定概率接受新解
if rand < exp(-(E_new-E_current)./t)
E_current = E_new;
sol_current = sol_new;
else
sol_new = sol_current;
end
end
end
t=t.*a; % 控制参数t(温度)减少为原来的a倍
end
for i=1:length(coordinates)
plot(coordinates(i,1),coordinates(i,2),'r*');
hold on;
end;
x=coordinates([sol_best sol_best(1)],1);
y=coordinates([sol_best sol_best(1)],2);
plot(x,y);
disp('最优解为:')
disp(sol_best)
disp('最短距离:')
disp(E_best)
以上代码来自:http://blog.csdn.net/zhangzhengyi03539/article/details/46673545
txt数据:
565 575
25 185
345 750
945 685
845 655
880 660
25 230
525 1000
580 1175
650 1130
1605 620
1220 580
1465 200
1530 5
845 680
725 370
145 665
415 635
510 875
560 365
300 465
520 585
480 415
835 625
975 580
1215 245
1320 315
1250 400
660 180
410 250
420 555
575 665
1150 1160
700 580
685 595
685 610
770 610
795 645
720 635
760 650
475 960
95 260
875 920
700 500
555 815
830 485
1170 65
830 610
605 625
595 360
1340 725
1740 245