Splay

引入

BST(二叉排序树)

一棵空树，或者是具有下列性质的二叉树：

1. 若左子树不空，则左子树上所有结点的值均小于它的根结点的值；
2. 若右子树不空，则右子树上所有结点的值均大于它的根结点的值；
3. 左、右子树也分别为二叉排序树；
4. 没有编号相等的结点。

但是当插入数据有序时， BST会退化为一条链， 时间复杂度就会变为(O(n)), 所以就有了平衡树

平衡树

在保证BST的性质不变的情况下， 将树结构进行变换， 使树结构接近完全二叉树， 使查询时间复杂度为(O(log n))。

Splay(伸展树)

假设想要对一个二叉查找树执行一系列的查找操作。为了使整个查找时间更小，被查频率高的那些条目就应当经常处于靠近树根的位置。于是想到设计一个简单方法， 在每次查找之后对树进行重构，把被查找的条目搬移到离树根近一些的地方。splay tree应运而生。splay tree是一种自调整形式的二叉查找树，它会沿着从某个节点到树根之间的路径，通过一系列的旋转把这个节点搬移到树根去。

基本操作

本文代码变量含义

1. ch[x][k] : 编号为(x)的节点的子节点的编号。当(k=0)， 存储左子节点， 当(k=1), 存储右子节点。
2. cnt[x] : 相同的点的存在个数
3. size[x] : 编号为(x)的子树的大小
4. v[x] : 编号为(x)的节点的值
5. f[x] : 编号为(x)的节点的父节点
6. root : 树的根
7. tot : 节点总数

更新

每次树的结构变化， 都要维护一下size

inline void update(int x) { size[x] = size[ch[x][0]] + size[ch[x][1]] + cnt[x]; }

(x)的子树大小为左右子节点的子树大小加其本身大小。

单旋

将某个节点向上旋转， 使其深度减小， 同时保证BST的性质不被破坏。

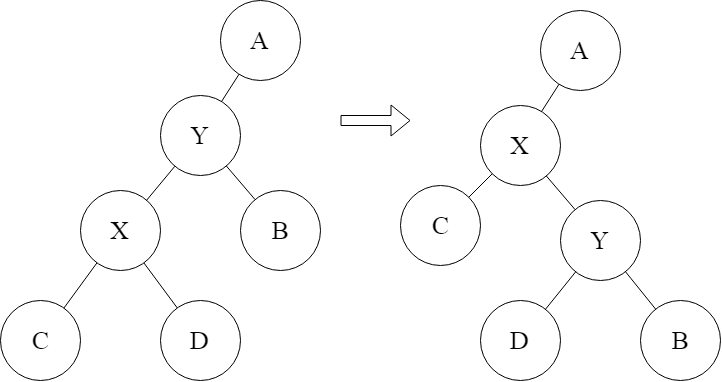
此图将(x)向上旋转

简单描述过程就是(x)旋转到(y)的位置， (x)的右子树变为(y)的左子树， (y)变为(x)的右子树， 其他不变。

当(x)为(y)的左子节点， 旋转操作如上图， 当(x)为(y)的右子节点， 旋转操作与上图对称。

void rotate (int x) {
	int y = f[x], z = f[y], k = (ch[y][1] == x); // k为x相对于y的位置
	ch[z][ch[z][1] == y] = x, f[x] = z; // x旋转到y的位置, 维护父亲
	ch[y][k] = ch[x][!k], f[ch[x][!k]] = y; // x的右子树变为y的左子树， 维护父亲
	ch[x][!k] = y, f[y] = x; // y变为x的右子树， 维护父亲
	update(y), update(x); // 先更新深度大的， 再更新深度小的
}

Splay(伸展)

splay就是把某个节点向上旋转若干次， 使节点到达某个位置

void splay (int x, int t) { //把x旋转到父亲为t的位置
	while (f[x] != t) { //x的父亲不为t就执行
		int y = f[x], z = f[y];
		if (z != t) (ch[y][0] == x) == (ch[z][0] == y) ? rotate(y) : rotate(x);  // 如果z-y-x方向一样， 就旋转y, 否则旋转x
		rotate(x); // 然后再旋转x
	}
	if (!t) root = x; // 如果旋转到了根节点， 更新根节点
}

为什么如果(z-y-x)方向一样(都向左偏或向右偏)， 就要旋转一下(y)呢？

自己画一下就会发现， 在这种情况下， 如果只旋转两次(x)， 有一条链结构没有变化， 而先旋转(y)再旋转(x)，就改变了所有链的结构和子树的深度。

这样更利于查询。

查找

void find (int x) {
	int u = root;
	while (ch[u][x > v[u]] && x != v[u]) u = ch[u][x > v[u]]; // 不断向下找
	splay(u, 0); // 把找到的点旋到根节点
}

有两点要注意：

1. 这个查找操作保证查找时树不为空， 因为为了避免越界， 减少边界情况的判断， 通常会先插入一个正无穷和负无穷， 所以查找时不用特殊判断， 否则要特判树为空的情况。
2. 当x > v[u], x > v[u] 为 1， ch[u][x > v[u]]为ch[u][1] 即其左子节点;
   当x < v[u], x > v[u] 为 0， ch[u][x > v[u]]为ch[u][0] 即其右子节点。
   所以u = ch[u][x > v[u]]就能一直向接近x的位置移动。

插入

void insert (int x) {
	int u = root, fa = 0;
	while (u && x != v[u]) fa = u, u = ch[u][x > v[u]]; //寻找接近x的位置
	if (u) cnt[u]++; // 如果存在， 增加其计数
	else {
		u = ++tot; // 分配编号
		if (fa) ch[fa][x > v[fa]] = u; // 更新父节点的信息
		v[u] = x, f[u] = fa, cnt[u] = size[u] = 1; //维护其他信息
	}
	splay(u, 0); // 别忘了splay
}

查找前驱

(x)的前驱定义为小于(x)，且最大的数。

先find(x)， (x)就成为根节点， 根据BST的性质， 比根节点小的数都在根节点的左子树里。 所以小于根节点，且最大的数就是根节点左子树的最大数。

int pre(int x) {
	find(x); // x旋转到根节点
	if (x > v[root]) return root; // 判断不存在的情况
	int u = ch[root][0]; // 找到其左子树
	if (!u) return -1; 
	while (ch[u][1]) u = ch[u][1]; // 不断找最大的
	return u;
}

查找后继

操作和求前驱类似

int nxt(int x) {
	find(x);
	if (x < v[root]) return root;
	int u = ch[root][1];
	if (!u) return -1;
	while (ch[u][0]) u = ch[u][0];
	return u;
}

删除

删除(x)时， 把(x)的前驱旋转到根节点， 后继旋转到根节点的右子节点， 因为(x)大于其前驱，所以(x)在根节点的右子树；而(x)小于其后继， 所以(x)是根节点的右子树的左子节点。

注意根节点的右子树的左子树有且只有(x), 因为只有(x)大于(x)的前驱且小于(x)的后继。

void del(int x) {
	int px = pre(x), nx = nxt(x); //求前驱后继
	splay(px, 0), splay(nx, root); // 把x的前驱旋转到根节点， 后继旋转到根节点的右子节点
	int u = ch[nx][0];
	if (cnt[u] > 1) cnt[u]--, splay(u, 0); // 如果有多个， 减去并splay
	else ch[nx][0] = 0, update(r), update(l); //直接删除
}

查找第k大

根据之前维护的size查询第(k)大

int findk (int x) {
	int u = root;
	if (size[u] < x) return -1;
	while (1) {
		if (x <= size[ch[u][0]]) u = ch[u][0]; // 右子树大小大于查询排名， 向右子树查询
		else if (x > size[ch[u][0]] + cnt[u]) x -= size[ch[u][0]] + cnt[u], u = ch[u][1]; // 右子树大小+本身大小小于查询排名， 向减一下
		else return u; // 否则就查到了， return即可
	}
}

查询x的排名

把查询节点旋转到根节点， 返回左子树的size即可， 注意左子树还有一个多余的负无穷， 所以不用减一。

int rank (int x) {
	find(x);
	return size[ch[root][0]];
}

例题

洛谷 P3369 普通平衡树

参考代码

#include <cstdio>
#define MAXN 100005
int ch[MAXN][2], cnt[MAXN], size[MAXN], v[MAXN], f[MAXN], root, tot;
inline void update(int x) { size[x] = size[ch[x][0]] + size[ch[x][1]] + cnt[x]; }
void rotate (int x) {
	int y = f[x], z = f[y], k = (ch[y][1] == x);
	ch[z][ch[z][1] == y] = x, f[x] = z;
	ch[y][k] = ch[x][!k], f[ch[x][!k]] = y;
	ch[x][!k] = y, f[y] = x;
	update(y), update(x);
}
void splay (int x, int t) {
	while (f[x] != t) {
		int y = f[x], z = f[y];
		if (z != t) (ch[y][0] == x) == (ch[z][0] == y) ? rotate(y) : rotate(x);
		rotate(x);
	}
	if (!t) root = x;
}
void find (int x) {
	int u = root;
	while (ch[u][x > v[u]] && x != v[u]) u = ch[u][x > v[u]];
	splay(u, 0);
}
void insert (int x) {
	int u = root, fa = 0;
	while (u && x != v[u]) fa = u, u = ch[u][x > v[u]];
	if (u) cnt[u]++;
	else {
		u = ++tot;
		if (fa) ch[fa][x > v[fa]] = u;
		v[u] = x, f[u] = fa, cnt[u] = size[u] = 1;
	}
	splay(u, 0);
}
int pre(int x) {
	find(x);
	if (x > v[root]) return root;
	int u = ch[root][0];
	if (!u) return -1;
	while (ch[u][1]) u = ch[u][1];
	return u;
}
int nxt(int x) {
	find(x);
	if (x < v[root]) return root;
	int u = ch[root][1];
	if (!u) return -1;
	while (ch[u][0]) u = ch[u][0];
	return u;
}
void del(int x) {
	int xp = pre(x), xn = nxt(x);
	splay(xp, 0), splay(xn, root);
	int u = ch[xn][0];
	if (cnt[u] > 1) cnt[u]--, splay(u, 0);
	else ch[nx][0] = 0, update(r), update(l);
}
int findk (int x) {
	int u = root;
	if (size[u] < x) return -1;
	while (1) {
		if (x <= size[ch[u][0]]) u = ch[u][0];
		else if (x > size[ch[u][0]] + cnt[u]) x -= size[ch[u][0]] + cnt[u], u = ch[u][1];
		else return u;
	}
}
int rank (int x) {
	find(x);
	return size[ch[root][0]];
}
int main () {
	int n, op, x;
	scanf("%d", &n);
	insert(-10000005), insert(10000005); //插入正无穷和负无穷
	for (int i = 1; i <= n; i++) {
		scanf("%d%d", &op, &x);
		if (op == 1) insert(x);
		else if (op == 2) del(x);
		else if (op == 3) printf("%d
", rank(x));
		else if (op == 4) printf("%d
", v[findk(x + 1)]); // 别忘了还有一个负无穷占位， 排名要+1
		else if (op == 5) printf("%d
", v[pre(x)]);
		else printf("%d
", v[nxt(x)]);
	}
	return 0;
}