The k-medoids algorithm is a clustering algorithm related to the k-means algorithm and the medoidshift algorithm. Both the k-means and k-medoids algorithms are partitional (breaking the dataset up into groups) and both attempt to minimize the distance between points labeled to be in a cluster and a point designated as the center of that cluster. In contrast to the k-means algorithm, k-medoids chooses datapoints as centers (medoids or exemplars) and works with an arbitrary matrix of distances between datapoints instead of 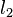 . This method was proposed in 1987[1] for the work with
. This method was proposed in 1987[1] for the work with  norm and other distances.
norm and other distances.
k-medoid is a classical partitioning technique of clustering that clusters the data set of n objects into k clusters known a priori. A useful tool for determining k is the silhouette.
It is more robust to noise and outliers as compared to k-means because it minimizes a sum of pairwise dissimilarities instead of a sum of squared Euclidean distances.
A medoid can be defined as the object of a cluster, whose average dissimilarity to all the objects in the cluster is minimal i.e. it is a most centrally located point in the cluster.
The most common realisation of k-medoid clustering is the Partitioning Around Medoids (PAM) algorithm and is as follows:[2]
- Initialize: randomly select k of the n data points as the medoids
- Associate each data point to the closest medoid. ("closest" here is defined using any valid distance metric, most commonly Euclidean distance, Manhattan distance or Minkowski distance)
- For each medoid m
- For each non-medoid data point o
- Swap m and o and compute the total cost of the configuration
- For each non-medoid data point o
- Select the configuration with the lowest cost.
- repeat steps 2 to 4 until there is no change in the medoid.
看起来和K-means比较相似,但是K-medoids和K-means是有区别的,不一样的地方在于中心点的选取,在K-means中,我们将中心点取为当前cluster中所有数据点的平均值,在 K-medoids算法中,我们将从当前cluster 中选取这样一个点——它到其他所有(当前cluster中的)点的距离之和最小——作为中心点。
K-MEANS算法的缺点:
产生类的大小相差不会很大,对于脏数据很敏感。
改进的算法:K-medoids方法。
这儿选取一个对象叫做mediod来代替上面的中心的作用,这样的一个medoid就标识了这个类。
K-MEDODIS的具体流程如下:
1)任意选取K个对象作为medoids(O1,O2,…Oi…Ok)。
2)将余下的对象分到各个类中去(根据与medoid最相近的原则);
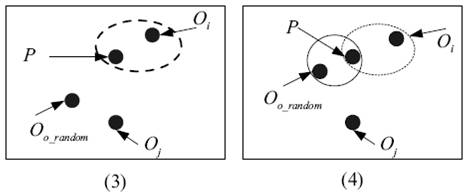
3)对于每个类(Oi)中,顺序选取一个Or,计算用Or代替Oi后的消耗—E(Or)。选择E最小的那个Or来代替Oi。这样K个medoids就改变了。
4)重复2、3步直到K个medoids固定下来。
不容易受到那些由于误差之类的原因产生的脏数据的影响,但计算量显然要比K-means要大,一般只适合小数据量。
http://en.wikipedia.org/wiki/K-medoids