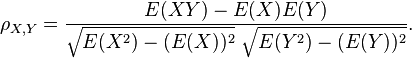在统计学中,皮尔逊积矩相关系数(英语:Pearson product-moment correlation coefficient,又称作 PPMCC或PCCs[1], 文章中常用r或Pearson's r表示)用于度量两个变量X和Y之间的相关(线性相关),其值介于-1与1之间。在自然科学领域中,该系数广泛用于度量两个变量之间的相关程度。它是由卡尔·皮尔逊从弗朗西斯·高尔顿在19世纪80年代提出的一个相似却又稍有不同的想法演变而来的。[2][3]这个相关系数也称作“皮尔森相关系数r”。
两个变量之间的皮尔逊相关系数定义为两个变量之间的协方差和标准差的商:
以上方程定义了总体相关系数, 一般表示成希腊字母ρ(rho)。基于样本对协方差和标准差进行估计,可以得到样本相关系数, 一般表示成r:
一种等价表达式的是表示成标准分的均值。基于(Xi, Yi)的样本点,样本皮尔逊系数是
其中
 、
、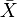 及
及 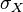
数学特性
总体和样本皮尔逊系数的绝对值小于或等于1。如果样本数据点精确的落在直线上(计算样本皮尔逊系数的情况),或者双变量分布完全在直线上(计算总体皮尔逊系数的情况),则相关系数等于1或-1。皮尔逊系数是对称的:corr(X,Y) = corr(Y,X)。
皮尔逊相关系数有一个重要的数学特性是,因两个变量的位置和尺度的变化并不会引起该系数的改变,即它该变化的不变量 (由符号确定)。也就是说,我们如果把X移动到a + bX和把Y移动到c + dY,其中a、b、c和d是常数,并不会改变两个变量的相关系数(该结论在总体和样本皮尔逊相关系数中都成立)。我们发现更一般的线性变换则会改变相关系数:参见之后章节对该特性应用的介绍。
由于μX = E(X), σX2 = E[(X − E(X))2] = E(X2) − E2(X),Y也类似, 并且
故相关系数也可以表示成
对于样本皮尔逊相关系数:
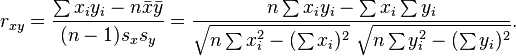
- 相关python代码:
-
critics={'Lisa Rose': {'Lady in the Water': 2.5, 'Snakes on a Plane': 3.5,
'Just My Luck': 3.0, 'Superman Returns': 3.5, 'You, Me and Dupree': 2.5,
'The Night Listener': 3.0},
'Gene Seymour': {'Lady in the Water': 3.0, 'Snakes on a Plane': 3.5,
'Just My Luck': 1.5, 'Superman Returns': 5.0, 'The Night Listener': 3.0,
'You, Me and Dupree': 3.5}}critics是一个二维字典,一维表示某个人,二维表示某人对所看电影的评分。
现在要利用皮卡尔相关系数来求某2个人的相似度,代码如下:
def sim_pearson(prefs,p1,p2): #得到双方都评价过的物品列表 si={} for item in prefs[p1]: if item in prefs[p2]:si[item]=1 n=len(si) if n==0:return 1 #对所有偏好求和 sum1=sum([prefs[p1][it] for it in si]) sum2=sum([prefs[p2][it] for it in si]) #求乘积之和 pSum=sum([prefs[p1][it]*prefs[p2][it] for it in si]) #求平方和 sum1Sq=sum([pow(prefs[p1][it],2) for it in si]) sum2Sq=sum([pow(prefs[p2][it],2) for it in si]) num=n*pSum-sum1*sum2 den1=sqrt(n*sum1Sq-pow(sum1,2)) den2=sqrt(n*sum2Sq-pow(sum2,2)) den=den1*den2 if den==0:return 0 r=num/den return r
以上方程给出了计算样本皮尔逊相关系数简单的单流程算法,但是其依赖于涉及到的数据,有时它可能是数值不稳定的。
解释
皮尔逊相关系数的变化范围为-1到1。 系数的值为1意味着X 和 Y可以很好的由直线方程来描述,所有的数据点都很好的落在一条 直线上,且 Y 随着 X 的增加而增加。系数的值为−1意味着所有的数据点都落在直线上,且 Y 随着 X 的增加而减少。系数的值为0意味着两个变量之间没有线性关系。
更一般的, 我们发现,当且仅当 Xi and Yi 均落在他们各自的均值的同一侧, 则(Xi − X)(Yi − Y) 的值为正。 也就是说,如果Xi 和 Yi 同时趋向于大于, 或同时趋向于小于他们各自的均值,则相关系数为正。 如果 Xi 和 Yi 趋向于落在他们均值的相反一侧,则相关系数为负。
via:http://zh.wikipedia.org/wiki/%E7%9A%AE%E5%B0%94%E9%80%8A%E7%A7%AF%E7%9F%A9%E7%9B%B8%E5%85%B3%E7%B3%BB%E6%95%B0
![\rho_{X,Y}={\mathrm{cov}(X,Y) \over \sigma_X \sigma_Y} ={E[(X-\mu_X)(Y-\mu_Y)] \over \sigma_X\sigma_Y},](http://upload.wikimedia.org/math/1/7/7/17709e96782a6a8bcd39904c5f2383e6.png)
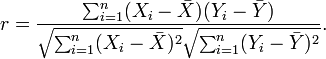

![E[(X-E(X))(Y-E(Y))]=E(XY)-E(X)E(Y),\,](http://upload.wikimedia.org/math/d/6/8/d68b84931c79ab42b6a9374ffd5a4179.png)