由结构体组成的表与结构体中的表。
在用追溯形式建立家家谱树时,我们通常从某个后代除法,依次处理它的父母,组父母等。而构建树时,我们会不断添加谁是谁的孩子,而不是写出谁是谁的父母,从而建立一颗后代家谱树。
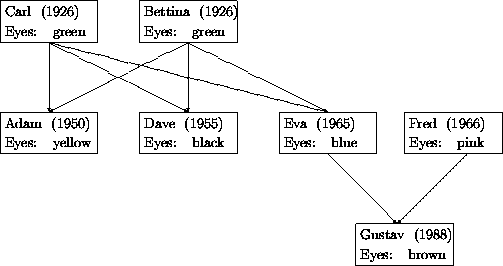
绘制后代数与绘制祖先树一样,只是将所有箭头的方向都反了过来:
(define-struct parent (children name date eyes))
children数量不固定,怎么办?
自然的选择是另children代表由parent结构体组成的表,这个表代表孩子,
parent是结构体:
(make-parent loc n d e) loc是孩子的表。
不幸的是,这个数据定义违反了我们关于定义的标准,具体说,他提到了一个还没定义的集合:孩子的表。
既然无法在不知道孩子的表示什么的情况下定义父母类型,我们就先定义孩子的表:
list of childrens 是下列之一
1 empty
2 (cons p loc);其中p是parent,loc是孩子的表。
第二个定义时标准的,但是他遇到和parent一样的问题。
结论是,这2个定义在相互引用对方,他们只在同时定义的情况下才有意义:
hen two (or more) data definitions refer to each other, they are said to be MUTUALLY RECURSIVE or MUTUALLY REFERENTIAL.
如果2个或更多的数据定义相互引用,我们就称他们为相互引用的。
现在,我们可以把上图中的家谱树转成scheme表达式了,当然,在建立parent结构体之前,必须先定义所偶有表示其孩子的阶段,最好的方法是,在使用某个parent结构体之前先给他命名,如:
(define Gustav (make-parent empty 'Gustav 1988 'brown)) (make-parent (list Gustav) 'Fred 1950 'yellow)
To create a parent structure for Fred, we first define one for Gustav so that we can form (list Gustav), the list of children for Fred.
完整定义:
;; Youngest Generation: (define Gustav (make-parent empty 'Gustav 1988 'brown)) (define Fred&Eva (list Gustav)) ;; Middle Generation: (define Adam (make-parent empty 'Adam 1950 'yellow)) (define Dave (make-parent empty 'Dave 1955 'black)) (define Eva (make-parent Fred&Eva 'Eva 1965 'blue)) (define Fred (make-parent Fred&Eva 'Fred 1966 'pink)) (define Carl&Bettina (list Adam Dave Eva)) ;; Oldest Generation: (define Carl (make-parent Carl&Bettina 'Carl 1926 'green)) (define Bettina (make-parent Carl&Bettina 'Bettina 1926 'green)) Figure 41: A Scheme representation of the descendant family tree
现在我们来研究blue-eyed-descendent?的开发,他是blue-eyed-ancestor的自然对应物,该函数读入一个parent结构体,判断他或货代是否有眼睛是蓝色的。下面的有点难,我最开始试图只用一个函数来搞定,发现始终不行,看了答案才知道:
;; blue-eyed-descendant? : parent -> boolean ;; to determine whether a-parent any of the descendants (children, ;; grandchildren, and so on) have 'blue in the eyes field (define (blue-eyed-descendant? a-parent) (cond [(symbol=? (parent-eyes a-parent) 'blue) true] [else (blue-eyed-children? (parent-children a-parent))])) ;; blue-eyed-children? : list-of-children -> boolean ;; to determine whether any of the structures in aloc is blue-eyed ;; or has any blue-eyed descendant (define (blue-eyed-children? aloc) (cond [(empty? aloc) false] [else (cond [(blue-eyed-descendant? (first aloc)) true] [else (blue-eyed-children? (rest aloc))])])) ;; blue-eyed-descendant? : parent -> boolean ;; to determine whether a-parent any of the descendants (children, ;; grandchildren, and so on) have 'blue in the eyes field (define (blue-eyed-descendant? a-parent) (or (symbol=? (parent-eyes a-parent) 'blue) (blue-eyed-children? (parent-children a-parent)))) ;; blue-eyed-children? : list-of-children -> boolean ;; to determine whether any of the structures in aloc is blue-eyed ;; or has any blue-eyed descendant (define (blue-eyed-children? aloc) (cond [(empty? aloc) false] [else (or (blue-eyed-descendant? (first aloc)) (blue-eyed-children? (rest aloc)))])) Figure 42: Two programs for finding a blue-eyed descendant
Exercise 15.1.2. Develop the function how-far-removed. It determines how far a blue-eyed descendant, if one exists, is removed from the given parent. If the given parent has blue eyes, the distance is 0; if eyes is not blue but at least one its children's eyes are, the distance is 1; and so on. If no descendant of the given parent has blue eyes, the function returns false when it is applied to the corresponding family tree. ![]() Solution
Solution
;; A parent is a structure: (make-parent loc n d e) ;; where loc is a list of children, ;; n and e are symbols, and d is a number. (define-struct parent (children name date eyes)) ;; A list of children is either ;; 1. empty or ;; 2. (cons p loc) where p is a parent and loc is a list of children. ;; EXAMPLES OF DATA (define robby (make-parent empty "Robby" 1972 'blue)) (define ted (make-parent empty "Ted" 1975 'brown)) (define pat (make-parent empty "Pat" 1978 'brown)) (define pete (make-parent empty "Pete" 1982 'brown)) (define alice (make-parent (list robby ted pat pete) "Alice" 1949 'blue)) (define bill (make-parent (list robby ted pat pete) "Bill" 1949 'brown)) (define lolly (make-parent empty "Lolly" 1951 'blue)) (define tutu (make-parent (list alice lolly) "Tutu" 1911 'brown)) ;; how-far-removed : parent -> number or false ;; to find the distance to the nearest blue eyed descendent ;; or return false if there is no such descendant (define (how-far-removed a-parent) (cond [(symbol=? 'blue (parent-eyes a-parent)) 0] [else (add1/false (how-far-removed-children (parent-children a-parent)))])) ;; how-far-removed-children : list of children -> number or false ;; to find the nearest blue eyed descent for a list of children, ;; assuming that one exists (define (how-far-removed-children children) (cond [(empty? children) false] [else (min/false (how-far-removed (first children)) (how-far-removed-children (rest children)))])) ;; add1/false : number or false -> number or false ;; to add one to a number, or return false (define (add1/false n) (cond [(number? n) (+ n 1)] [else false])) ;; min/false : (number or false) (number or false) -> (number or false) ;; to compute the minimum number of two numbers ;; if both are numbers, find the minimum. ;; if only one is a number, return that. ;; if both are false, return false. (define (min/false n m) (cond [(and (number? n) (number? m)) (min n m)] [(and (number? n) (boolean? m)) n] [(and (boolean? n) (number? m)) m] [(and (boolean? n) (boolean? m)) false])) ;; EXAMPLES AS TESTS (how-far-removed ted) "should be" false (how-far-removed robby) "should be" 0 (how-far-removed alice) "should be" 0 (how-far-removed bill) "should be" 1 (how-far-removed tutu) "should be" 1
Exercise 15.1.3. Develop the function count-descendants, which consumes a parent and produces the number of descendants, including the parent.
Develop the function count-proper-descendants, which consumes a parent and produces the number of proper descendants, that is, all nodes in the family tree, not counting the parent. ![]() Solution
Solution
(define (count-descendants a-parent) (cond [(empty? (parent-children a-parent)) 1] [else (+ 1 (count-children (parent-children a-parent)))] ) ) ;; count-children : list-of-children -> number ;; consumes a list-of-children c ;; produces the number of parents in c (define (count-children a-loc) (cond [(empty? a-loc) 0] [else (+ (count-descendants (first a-loc)) (count-children (rest a-loc)))])) (count-descendants Eva) 2 (count-descendants Carl) 5
(define (count-proper-descendants a-parent) (count-children (parent-children a-parent)) )
Exercise 15.1.4. Develop the function eye-colors, which consumes a parent and produces a list of all eye colors in the tree. An eye color may occur more than once in the list.
Hint: Use the Scheme operation append, which consumes two lists and produces the concatenation of the two lists. ![]() Solution
Solution
;; eye-colors : parent -> list ;; consumes a parent and produces a list of all eye colors in the tree (define (eye-colors a-parent) (cons (parent-eyes a-parent) (children-eyes (parent-children a-parent))) ) (define (children-eyes a-loc) (cond [(empty? a-loc) empty] [else (append (eye-colors (first a-loc)) (children-eyes (rest a-loc)) ) ] ) ) (eye-colors Carl)
相互递归
为相互引用的定义设计函数:
在上述例子中,我们需要2个相关的定义:
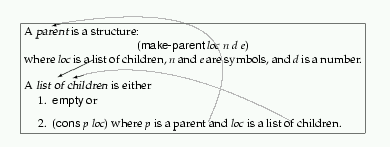
Templates:The templates are created in parallel, following the advice concerning compound data, mixed data, and self-referential data. Finally, we must determine for each selector expression in each template whether it corresponds to a cross-reference to some definition. If so, we annotate it in the same way we annotate cross-references.
Here are the templates for our running example:
模板被并行地创建。

fun-parent模板中没有条件,因为parent的数据定义中并不包含任何子句,而是包含对第二个模板的相互引用:处理parent结构体中的chidlren字段。按照同样的规则,fun-children是一个条件式,第2个cond子句中包含了一处自引用,处理表的rest部分,以及对表的first元素,即parent结构体-的一处相互引用。
对数据定义和模板的比较表明了他们是多么的类似。
15.3 网页再谈