Time Limit: 1000 ms Memory Limit: 128 MB
[吐槽]
点分治点分治点分治
嗯。。场上思考树状数组的时候好像傻掉了。。反正就是挂了就是了。。
[题解]
首先如果没有环的话就是一道十分简单的点分治啦
但是这题有环啊
考虑强行变树
从题目各种谜一般的描述中得出来的结论是:$m<=n$
其实也就是说最多只有一个环
那么就有一个很直接的想法,先把唯一的一个环找出来,断掉其中的一条边
这样就使它变成一棵树了,直接跑一遍点分就好
考虑断掉的那条边
这样统计有一个很明显的问题:经过断开那条边的情况全部都没有算进去
所以现在就考虑怎么算过这条边的ans
首先我们可以将这个环摊开变成这样:
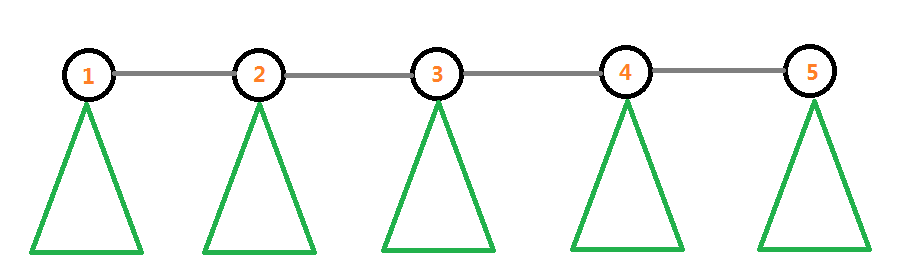
然后发现这个东西其实就是一条“链”上面有若干棵树
断开的那条边显然就是连接这条“链”一头一尾的边(为了方便描述,将这条断开的边记作$(x,y)$)
我们定义
$rt_i$表示$i$所属的子树的根节点
$dis_i$ 表示$i$到$rt_i$的的路径上的点数
$left_i$表示$rt_i$到这条“链”头(也就是图中编号为1的点)的节点数
$right_i$表述$rt_i$到这条“链”尾(图中编号为5的点)的节点数
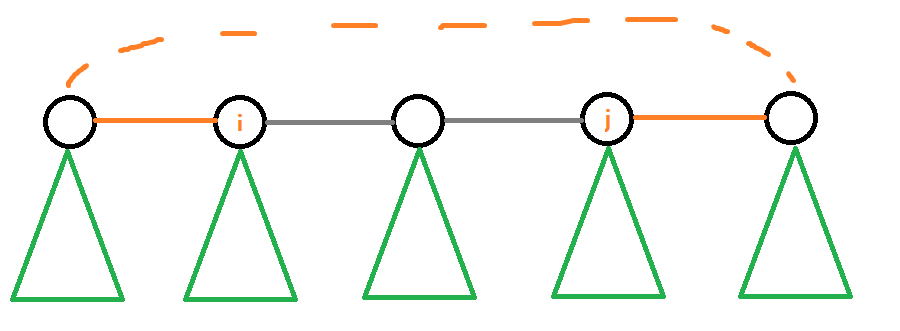
那么要算一条过$(x,y)$的路径$(i,j)$的点数的话,显然就是子树里面的距离+链上要走的距离
也就是 $dis_i+dis_j+left_i+right_j$ ($rt_i$在$rt_j$左边)
那么就可以用一个树状数组来搞定了
考虑怎么统计
(其实实现起来并不用上面的那些奇妙数组)
我们可以先将链上的点(也就是各个子树的根节点)编个号
那么对于一个这条链上面的第$i$和第$j$ $(i<j)$ 个点,那么链上要走的距离就为 $i+(len-j+1)$
其中$len$表示的是链的长度
然后将式子上一步中求路径上点数的式子稍微整理一下,得到
$(dis_i+i)+(dis_j+len-j+1) (i<j) $
所以我们可以从左往右一个一个点处理
先将当前点$i$子树内的$dis$处理出来
然后对于每一个$dis_j (j in subtree(i))$ ,在树状数组里面查询大于等于$k-dis_j-(len-j+1)$的数量(原因在后面解释)
查询完了之后将$dis_j+j$丢入树状数组中
这么处理的原因显然
整理过后的式子可以分为两部分,分别只与$i$和$j$有关
然后因为我们是从左到右处理链上面的点的,所以可以保证查询到的点是在当前点的前面的
然后这题就十分愉快地解决啦
[一些小细节]
因为这题是求>=的方案数
所以树状数组要十分愉快地反过来(也就是insert的时候是x-=x&-x,query的时候是x+=x&-x,见代码)
以及因为insert的时候是dis+i,所以上限应该是2*n
以及要用long long
嗯大概就是这样ovo

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #define ll long long 6 using namespace std; 7 const int MAXN=100010; 8 int h[MAXN],size[MAXN],mx[MAXN]; 9 ll dis[MAXN]; 10 bool vis[MAXN]; 11 int n,m,k,tot,rt,rt_mx; 12 ll ans,num; 13 struct xxx 14 { 15 int y,next; 16 bool flag; 17 }a[MAXN*2]; 18 struct data 19 { 20 ll c[MAXN*2]; 21 int insert(int x,ll delta) {_insert(x,delta);} 22 int _insert(int x,ll delta) 23 { 24 for (;x;x-=x&-x) c[x]+=delta; 25 } 26 ll query(int x) {return _query(x);} 27 ll _query(int x) 28 { 29 ll ret=0; 30 if (x<1) x=1; 31 for (;x<=2*n;x+=x&-x) ret+=c[x]; 32 return ret; 33 } 34 }c; 35 int pre[MAXN],cir[MAXN]; 36 int add(int x,int y); 37 int dfs(int x); 38 int dfs_size(int x,int fa); 39 int dfs_root(int r,int x,int fa); 40 int get_dis(int x,int fa,int d); 41 int get_cir(int fa,int x); 42 ll cal(int x,int d); 43 bool cmp(int x,int y){return x>y;} 44 int solve_cir(); 45 46 int main() 47 { 48 freopen("a.in","r",stdin); 49 freopen("a.out","w",stdout); 50 51 int x,y,z; 52 scanf("%d%d%d",&n,&m,&k); 53 tot=1; 54 memset(h,-1,sizeof(h)); 55 for (int i=1;i<=m;++i) 56 { 57 scanf("%d%d",&x,&y); 58 add(x,y); add(y,x); 59 } 60 if (m+1==n) {dfs(1); printf("%lld ",ans); return 0;} 61 cir[0]=0; 62 get_cir(0,1); 63 solve_cir(); 64 } 65 66 int add(int x,int y) 67 { 68 a[++tot].y=y; a[tot].next=h[x]; h[x]=tot; a[tot].flag=true; 69 } 70 71 int dfs(int x) 72 { 73 rt=0,rt_mx=n; 74 dfs_size(x,0); 75 dfs_root(x,x,0); 76 ans=ans+cal(rt,0); 77 vis[rt]=true; 78 for (int i=h[rt];i!=-1;i=a[i].next) 79 if (!vis[a[i].y]&&a[i].flag) 80 { 81 ans=ans-cal(a[i].y,1); 82 dfs(a[i].y); 83 } 84 } 85 86 int dfs_size(int x,int fa) 87 { 88 size[x]=1; 89 mx[x]=0; 90 for (int i=h[x];i!=-1;i=a[i].next) 91 if (a[i].y!=fa&&!vis[a[i].y]&&a[i].flag) 92 { 93 dfs_size(a[i].y,x); 94 size[x]+=size[a[i].y]; 95 mx[x]=max(mx[x],size[a[i].y]); 96 } 97 } 98 99 int dfs_root(int r,int x,int fa) 100 { 101 mx[x]=max(mx[x],size[r]-size[x]); 102 if (rt_mx>mx[x]) rt_mx=mx[x],rt=x; 103 for (int i=h[x];i!=-1;i=a[i].next) 104 if (a[i].y!=fa&&!vis[a[i].y]&&a[i].flag) 105 dfs_root(r,a[i].y,x); 106 } 107 108 int get_dis(int x,int fa,int d) 109 { 110 dis[++num]=d; 111 for (int i=h[x];i!=-1;i=a[i].next) 112 if (a[i].y!=fa&&!vis[a[i].y]&&a[i].flag) 113 get_dis(a[i].y,x,d+1); 114 } 115 116 ll cal(int x,int d) 117 { 118 num=0; 119 get_dis(x,0,d); 120 int left=1,right=num; 121 ll re=0; 122 sort(dis+1,dis+1+num,cmp); 123 while (left<right) 124 { 125 while (dis[left]+dis[right]+1<k&&left<right) --right; 126 re+=right-left; 127 ++left; 128 } 129 return re; 130 } 131 132 int get_cir(int fa,int x) 133 { 134 int u; 135 vis[x]=true; pre[x]=fa; 136 for (int i=h[x];i!=-1;i=a[i].next) 137 { 138 u=a[i].y; 139 if (u==fa) continue; 140 if (vis[u]) 141 { 142 a[i].flag=false; a[i^1].flag=false; 143 for (int j=x;j!=u;j=pre[j]) cir[++cir[0]]=j; 144 cir[++cir[0]]=u; 145 return 0; 146 } 147 get_cir(x,u); 148 if (cir[0]) return 0; 149 } 150 } 151 152 int solve_cir() 153 { 154 for (int i=1;i<=n;++i) vis[i]=false; 155 dfs(1); 156 for (int i=1;i<=n;++i) vis[i]=false; 157 for (int i=1;i<=cir[0];++i) vis[cir[i]]=true; 158 for (int i=1;i<=cir[0];++i) 159 { 160 num=0; 161 get_dis(cir[i],0,0); 162 for (int j=1;j<=num;++j) 163 ans+=c.query(k-dis[j]-(cir[0]-i+1)); 164 for (int j=1;j<=num;++j) 165 c.insert(dis[j]+i,1); 166 } 167 printf("%lld ",ans); 168 }