树概念:
树是n(n>=0)个结点的有限集。
其中n=0的树称为空数
树的特点:(非空数中)
(1) 有且仅有一个根节点
(2) 当n>1时,其余结点可分为m(m>0)个互不相交的有限集 T1,T2......Tn,其中每一个集合本身又是一颗树,并且称为根的子树
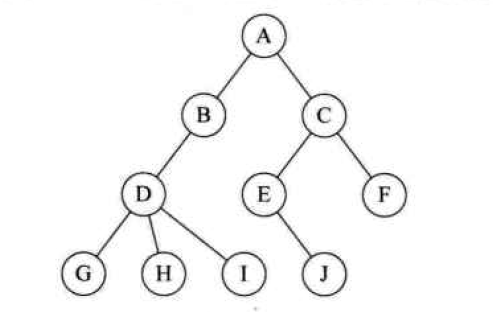
结点的度:
概念 : 结点拥有的子树称为结点的度
其中 度为0的结点称为叶子节点或终端结点
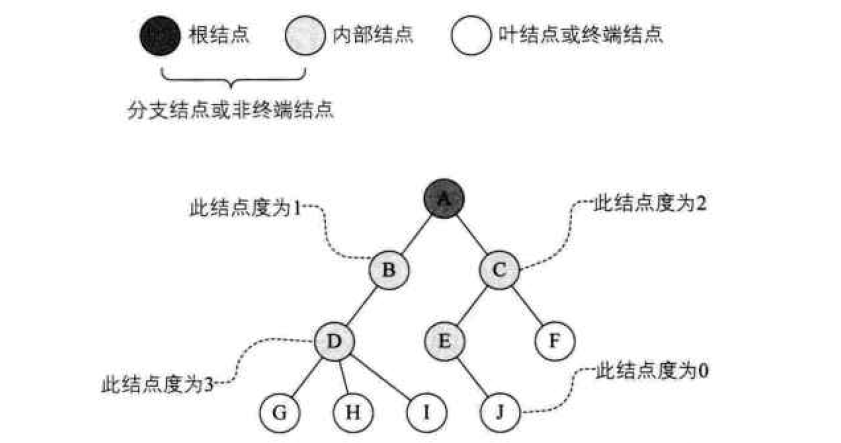
层次与深度


有序和无序树:
如果将树中结点的各子树看成从左到右是有次序的,不能互换的,则称该树为有序树,否则为无序树
树的存储结构:
结合顺序存储和链式存储来实现
三种表示方式
1) 、双亲表示法:

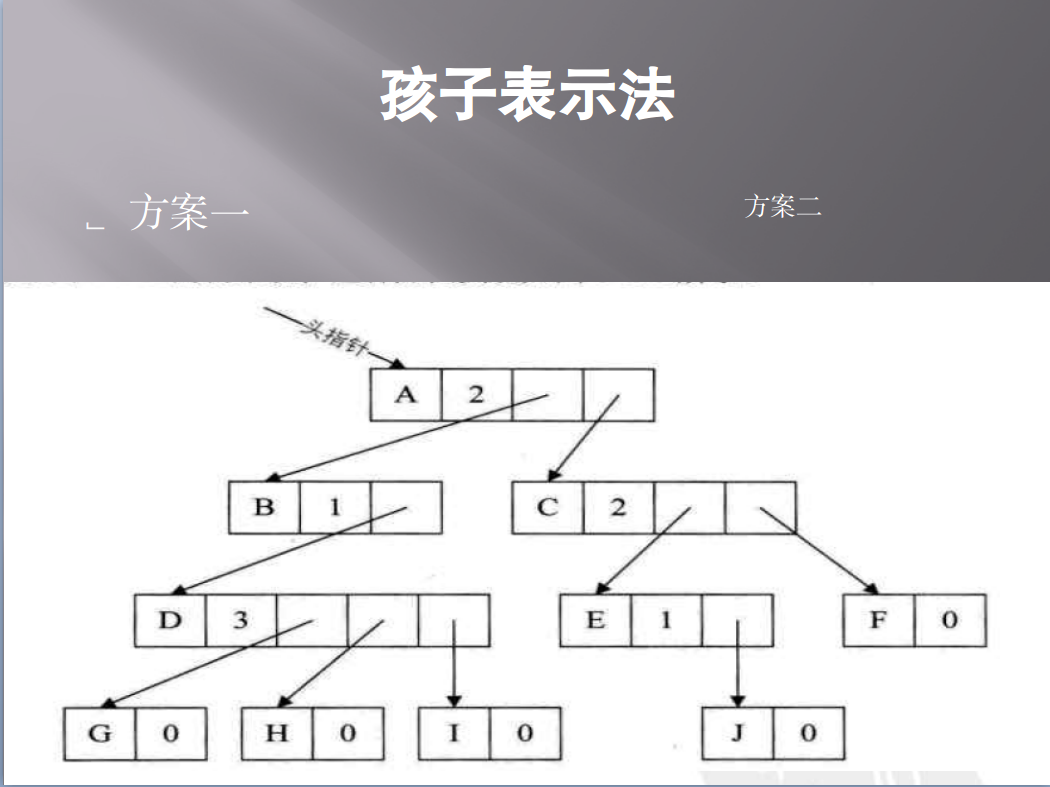
2)、孩子表示法:
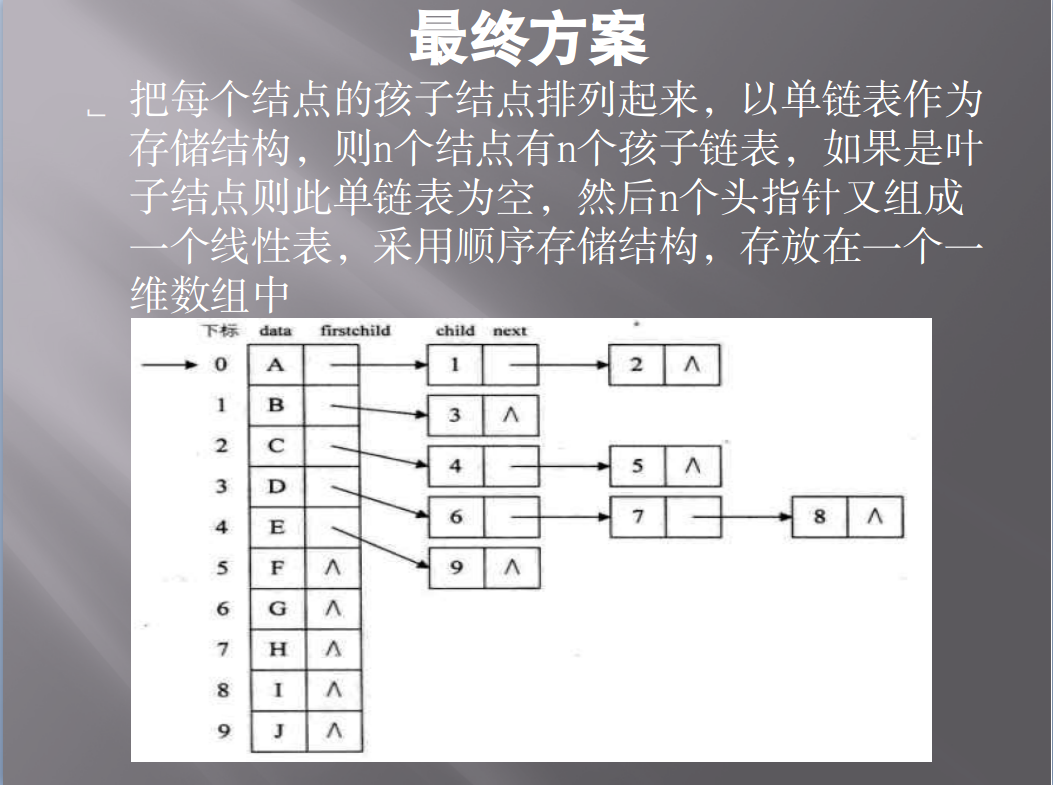
3)、最终方案
4)、孩子兄弟表示法:
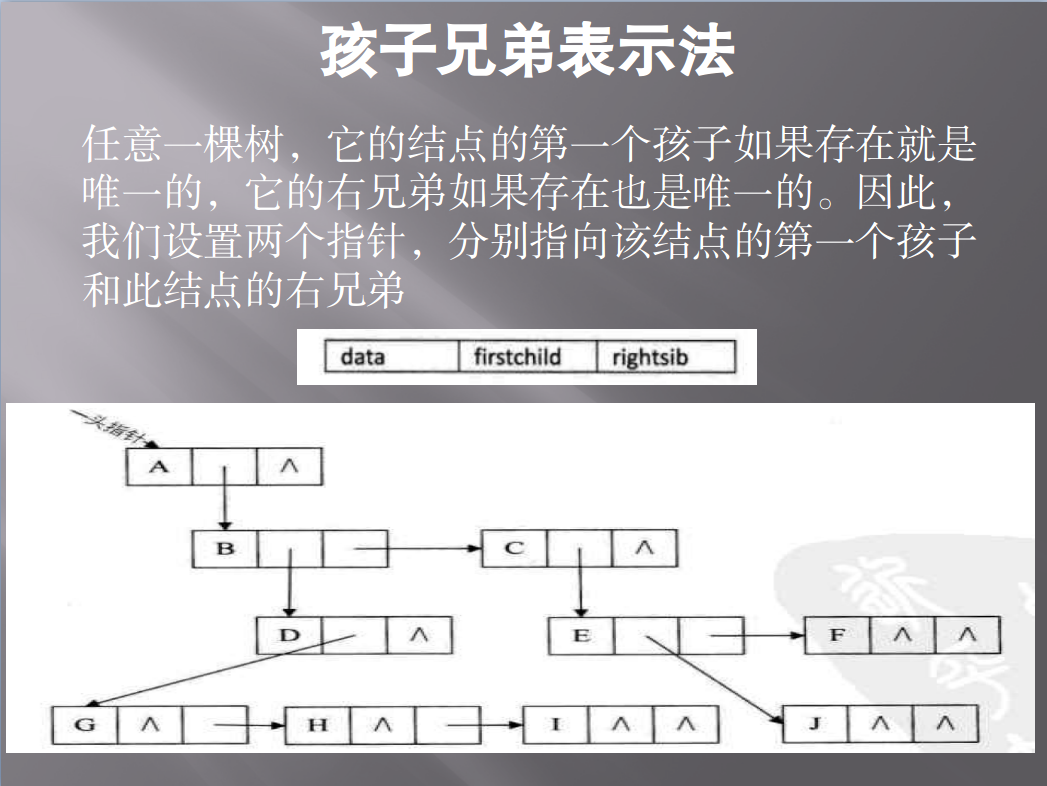
二叉树:
概念:
二叉树是n(n>=0)个结点的有限集合,该集合或者为空集(称为空二叉树),或者是由一个根结点和两颗互不相交的,分别称为根节点的左子树和
右子树的二叉树组成。
满二叉树:
概念:
在一颗二叉树中,如果所有分支结点都存在左子树和右子树,并且所有叶子都在同一层上,这样的二叉树称为满二叉树
