以下为本人学习并查集的体会与总结。
并查集概念
并查集也被称为不相交集数据结构。顾名思义,并查集主要操作是合并与查询,它是把初始不相交的集合经过多次合并操作后合并为一个大集合,然后可以通过查询判断两个元素是否已经在同一个集合中了。
并查集的应用场景一般就是动态连通性的判断,例如判断网络中的两台电脑是否连通,在程序中判断两个变量名是否指向同一内存地址等。
并查集的实现
并查集的存储结构
并查集逻辑上是森林,我们可以选出一个根节点作为代表,其他子结点指向根结点表示都在同一片森林中。在这里,并不关心结点的子结点是谁,只关心父结点是谁,所以物理上可以简单用python的列表来表示并查集,列表的下标表示结点,列表元素的值表示父结点。
并查集的API
根据并查集的特性,可以设计以下api
class UnionFind(object): """并查集类""" def __init__(self, n): """长度为n的并查集""" def find(self, p): """查找p的根结点(祖先)""" def union(self, p, q): """连通p,q 让q指向p""" def is_connected(self, p, q): """判断pq是否已经连通"""
并查集的初始化
并查集的初始化有几种,无非就是用一种特殊的方式来表示初始的每一个元素都不相交,等待后续的合并操作。
第一种初始化方式是用列表的下标初始化对应位置的值,当一个并查集S[i] == i 时则判断它自己就是根结点。
def __init__(self, n): """长度为n的并查集""" self.uf = [i for i in range(n + 1)] # 列表0位置空出 self.sets_count = n # 判断并查集里共有几个集合, 初始化默认互相独立
第二种初始化方式将列表每一个结点初始化为-1,列表的结点值为负数表示它自己就是根结点,这样做还有一个好处可以用-n表示自己的子结点的数量,下面的按规模优化中可以让结点数量小的树并到结点多的树上,提高find操作的效率。我们就选用这种方式来初始化。
def __init__(self, n): """长度为n的并查集""" self.uf = [-1 for i in range(n + 1)] # 列表0位置空出 self.sets_count = n # 判断并查集里共有几个集合, 初始化默认互相独立
并查集的查询
查询操作是查找某个结点所在的集合,返回该集合的根结点,即返回列表的下标。下面是一种简单的查询,代码如下。
def find(self, p): while self.uf[p] >= 0: p = self.uf[p] return p
可以很清楚的看出上面的方法很简单,找到结点元素值为负的表示找到了根结点并返回,但是该种方法在极端情况下(由树退化为链表)效率不高,查找的效率为O(n),如下左图所示

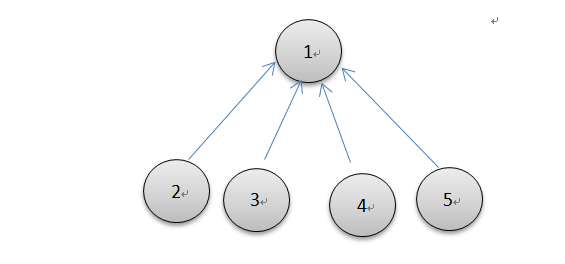
查询是并查集核心操作之一,它的效率也决定了整个算法的效率,所以在规模很大的情况下,O(n)的时间复杂度是不被接受的,那就需要改进,改进的方法就是路径压缩。路径压缩的思想也很简单,就是在查找根结点的过程中,顺便把子结点的父结点改成根结点,这样下次查询的效率只需要o(1)的时间复杂度就可以完成,大大提高了效率。改进后效果图如上右图所示。
路径压缩的find操作可以通过递归实现
def find(self, p): """尾递归""" if self.uf[p] < 0: return p self.uf[p] = self.find(self.uf[p]) return self.uf[p]
可以发现这个递归是尾递归,可以改进成循环的方式
def find(self, p): """查找p的根结点(祖先)""" r = p # 初始p while self.uf[p] > 0: p = self.uf[p] while r != p: # 路径压缩, 把搜索下来的结点祖先全指向根结点 self.uf[r], r = p, self.uf[r] return p
并查集的合并
合并两棵树的操作可以简单的规定让右边的树的根结点指向左边树的根结点,示意图如下左图所示。

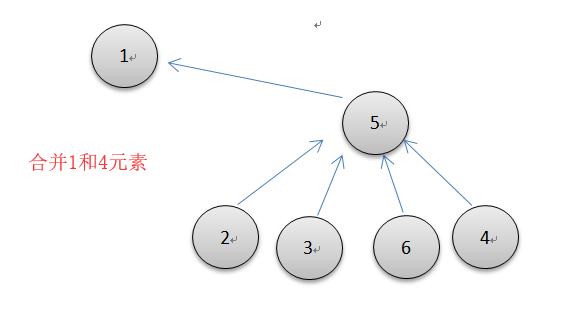
直接右往左合并的缺点就是当右边的规模大于左边的规模时,在查找时,做路径压缩需要把右边所有的根结点更改为左边的根结点,如上右图所示,这明显有些划不来,所以合并的一种优化方式就是按规模合并,即把规模小的树往规模大的树上合并。其实还有一种按秩合并(树高度小的往高度大的合并而不改变树的整体高度),但是这种方法不与路径压缩兼容,因为路径压缩直接改变了树的高度,所以本人选择按规模合并和路径压缩结合的方式优化并查集。代码如下
def union(self, p, q): """连通p,q 让q指向p""" proot = self.find(p) qroot = self.find(q) if proot == qroot: return elif self.uf[proot] > self.uf[qroot]: # 负数比较, 左边规模更小 self.uf[qroot] += self.uf[proot] self.uf[proot] = qroot else: self.uf[proot] += self.uf[qroot] # 规模相加 self.uf[qroot] = proot self.sets_count -= 1 # 连通后集合总数减一
连通性的判断
有了查找操作,判断两个结点是否连通就显得容易多了,一行代码就可以搞定,就是判断他们的根结点是否相同。
def is_connected(self, p, q): """判断pq是否已经连通""" return self.find(p) == self.find(q) # 即判断两个结点是否是属于同一个祖先
完整代码附录

1 class UnionFind(object): 2 """并查集类""" 3 def __init__(self, n): 4 """长度为n的并查集""" 5 self.uf = [-1 for i in range(n + 1)] # 列表0位置空出 6 self.sets_count = n # 判断并查集里共有几个集合, 初始化默认互相独立 7 8 # def find(self, p): 9 # """查找p的根结点(祖先)""" 10 # r = p # 初始p 11 # while self.uf[p] > 0: 12 # p = self.uf[p] 13 # while r != p: # 路径压缩, 把搜索下来的结点祖先全指向根结点 14 # self.uf[r], r = p, self.uf[r] 15 # return p 16 17 # def find(self, p): 18 # while self.uf[p] >= 0: 19 # p = self.uf[p] 20 # return p 21 22 def find(self, p): 23 """尾递归""" 24 if self.uf[p] < 0: 25 return p 26 self.uf[p] = self.find(self.uf[p]) 27 return self.uf[p] 28 29 def union(self, p, q): 30 """连通p,q 让q指向p""" 31 proot = self.find(p) 32 qroot = self.find(q) 33 if proot == qroot: 34 return 35 elif self.uf[proot] > self.uf[qroot]: # 负数比较, 左边规模更小 36 self.uf[qroot] += self.uf[proot] 37 self.uf[proot] = qroot 38 else: 39 self.uf[proot] += self.uf[qroot] # 规模相加 40 self.uf[qroot] = proot 41 self.sets_count -= 1 # 连通后集合总数减一 42 43 def is_connected(self, p, q): 44 """判断pq是否已经连通""" 45 return self.find(p) == self.find(q) # 即判断两个结点是否是属于同一个祖先
参考
其他并查集
普通的并查集只是简单的记录了和集合的关系,即判断是否属于该集合,而带权并查集则是不近记录了和集合的关系,还记录了集合内元素的关系,一般就是指代集合内元素和根结点的关系,实现起来也很简单,就是额外利用一个列表value[], 来记录每个结点与根结点的关系。然后在每次合并和路径压缩中更新权值。更新的规则遵循向量法则,处理环类关系的问题中,还可以取模更新。具体可以参考一下文章。
