1、引出问题
在前面讲解 HashMap 的源码实现时,有如下几点:
①、初始容量为 1<<4,也就是24 = 16

②、负载因子是0.75,当存入HashMap的元素占比超过整个容量的75%时,进行扩容,而且在不超过int类型的范围时,进行2次幂的扩展(指长度扩为原来2倍)

扩大一倍

③、新添加一个元素时,计算这个元素在HashMap中的位置,也就是本篇文章的主角 哈希运算。分为三步:
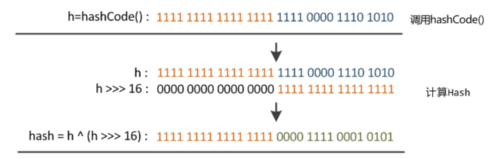
第一步:取 hashCode 值: key.hashCode()
第二步:高位参与运算:h>>>16
第三步:取模运算:(n-1) & hash
1 static final int hash(Object key) { 2 int h; 3 return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16); 4 } 5 6 tab[i = (n - 1) & hash];
ps:第 6 行代码是我自己加的。
我们知道一个好的 哈希算法能够使得元素分布的更加均匀,从而减少哈希冲突。HashMap 在这块的处理就很巧妙:
首先第一步取得 hashCode,该方法是一个用native修饰的本地方法,返回的是一个 int 类型的值(根据内存地址换算出来的一个值),通常我们都会重写该方法。
第二步将取得的哈希值无符号右移16位,高位补0。并与前面第一步获得的hash码进行按位异或^ 运算。这样做有什么用呢?这其实也是扰动函数,为了降低哈希码的冲突。右位移16位,正好是32bit的一半,高半区和低半区做异或,就是为了混合原始哈希码的高位和低位,以此来加大低位的随机性。而且混合后的低位掺杂了高位的部分特征,这样高位的信息也被变相保留下来。也就是保证考虑到高低Bit位都参与到Hash的计算中。
有兴趣的可以看看JDK1.7中,其实是做了4次扰动,在JDK1.8中只做了一次,我猜测是为了在降低冲突的同时保证效率。
本文的重点是第三步,将经过前面两步获取的 hash 值,与HashMap的集合长度减 1 进行按位与 & 运算:(n-1) & hash。但是其实很多哈希算法,为了使元素分布均匀,都是用的取模运算,用一个值去模上总长度,即 n%hash。我们知道在计算机中 & 的效率比 % 高很多,那么如何将 % 转换为 & 运算呢?在HashMap 中,是用的 (n - 1) & hash 进行运算的,那么这是为什么呢?
这就是本篇博客我们将要明白的问题。
2、结论
我们先给出结论:
当 lenth = 2n 时,X % length = X & (length - 1)
也就是说,长度为2的n次幂时,模运算 % 可以变换为按位与 & 运算。
比如:9 % 4 = 1,9的二进制是 1001 ,4-1 = 3,3的二进制是 0011。 9 & 3 = 1001 & 0011 = 0001 = 1
再比如:12 % 8 = 4,12的二进制是 1100,8-1 = 7,7的二进制是 0111。12 & 7 = 1100 & 0111 = 0100 = 4
上面两个例子4和8都是2的n次幂,结论是成立的,那么当长度不为2的n次幂呢?
比如:9 % 5 = 4,9的二进制是 1001,5-1 = 4,4的二进制是0100。9 & 4 = 1001 & 0100 = 0000 = 0。显然是不成立的。
为什么是这样?下面我们来详细分析。
3、分析过程
首先我们要知道如下规则:
①、"<<" 左移:右边空出的位上补0,左边的位将从字头挤掉,左移一位其值相当于乘2。
②、">>"右移:右边的位被挤掉,右移一位其值相当于除以2。对于左边移出的空位,如果是正数则空位补0,若为负数,可能补0或补1,这取决于所用的计算机系统。
③、">>>"无符号右移,右边的位被挤掉,对于左边移出的空位一概补上0。
根据二进制数的特点,相信大家很好理解。
对于给定一个任意的十进制数XnXn-1Xn-2....X1X0,我们将其用二进制的表示方法分解:
XnXn-1Xn-2....X1X0 = Xn*2n+Xn-1*2n-1+......+X1*21+X0*20 3-1公式
这里的十进制数只有三位,同理当有N位时,后面2的幂次方依次从 0 开始递增到 N 。
回到上面的结论: lenth = 2n 时,X % length = X & (length - 1)
以及对于除法,被除数是满足分配率的(除数不满足):
成立:(a+b)÷c=a÷c+b÷c 3-2公式
不成立:a÷(b+c)≠a÷c+b÷c
通过 3-1公式以及 3-2 公式,我们可以得出当任意一个十进制除以一个2k的数时,我们可以将这个十进制转换成3-1公式的表示形式:
(XnXn-1Xn-2....X1X0) / 2k = (Xn*2n+Xn-1*2n-1+......+X1*21+X0*20) / 2k = Xn*2n / 2k +Xn-1*2n-1 / 2k +......+ X1*21 / 2k + X0*20 / 2k
如果我们想求上面公式的余数,相信大家一眼就能看出来:
①、当 0<= k <= n 时,余数为 Xk*2k+Xk-1*2k-1+......+X1*21+X0*20 ,也就是说 比 k 大的 n次幂,我们都舍掉了(大的都能整除 2k),比k小的我们都留下来了(小的不能整除2k)。那么留来下来即为余数。
②、当 k > n 时,余数即为整个十进制数。
看到这里,我们离证明结论已经很近了。再回到上面说的二进制的移位操作,向右移 n 位,表示除以 2n 次方,由此我们得到一个很重要的结论:
一个十进制数对一个2n 的数取余,我们可以将这个十进制转换为二进制数,将这个二进制数右移n位,移掉的这 n 位数即是余数。
知道怎么算余数了,那么我们怎么去获取这移掉的 n 为数呢?
我们再看20,21,22....2n 用二进制表示如下:
0001,0010,0100,1000,10000......
我们把上面的数字减一:
0000,0001,0011,0111,01111......
根据与运算符&的规律,当位上都是 1 时,结果才是 1,否则为 0。所以任意一个二进制数对 2k 取余时,我们可以将这个二进制数与(2k-1)进行按位与运算,保留的即使余数。
这就完美的证明了前面给出的结论:
当 lenth = 2n 时,X % length = X & (length - 1)
注意,一定要是2n次方,才满足上面的公式,否则就是错误的。
4、总结
通过上面的分析过程了,我们完美了证明了公式的正确性。在回到 HashMap 的实现过程,我们知道HashMap的初始容量为啥是 1<<4 了吧,而且每次扩容都是扩大一倍。因为必须要完美的满足 hash 算法。