一、高级语言和机器指令中的运算
1、C程序中涉及的运算
按位运算
- C语言中的按位运算有:按位或|、按位与&、按位非~、按位异或^
- 按位运算是一种数值运算
逻辑运算
- C语言中的逻辑运算有:或||、与&&、非!
- 逻辑运算是非数值计算,其操作数只有两个逻辑值:True和False
移位运算
- 移位运算有两种:逻辑移位和算术移位
- 逻辑移位不考虑符号位,总是把高(低)位移出,低(高)位补0
- 带符号整数的移位操作采用补码算术移位方式
位扩展和位截断运算
- 进行数据类型转换时,遇到一个短数向长数转换,就要进行位扩展运算了
- 进行位扩展时,扩展后的数值应保持不变
- 两种位扩展方式:0扩展和符号扩展
- 0扩展用于无符号数,符号扩展用于补码表示的带符号整数
- 当一个长数足够大到短数无法表示的程度,则截断时就会发生溢出
二、基本运算部件
1、串行进位加法器
- 全加器用来实现两个本位数加上低位进位生成一位本位和以及一位向高位的进位
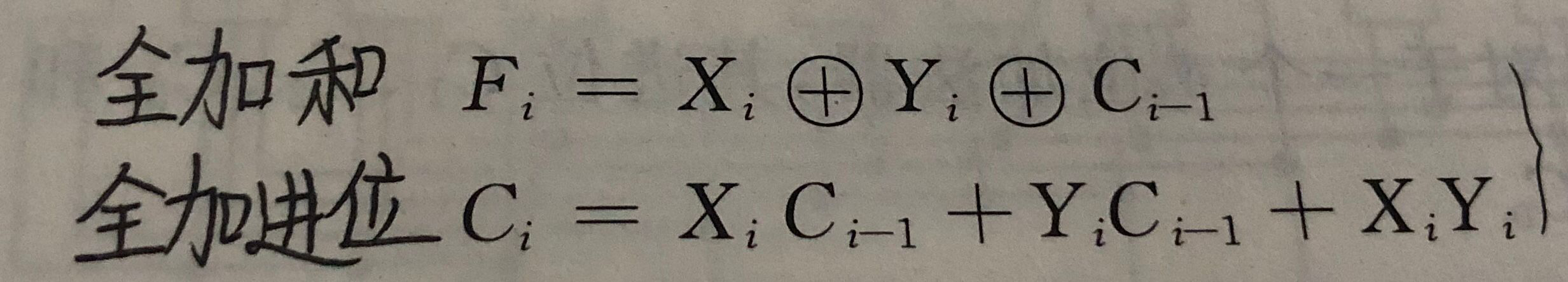
- 串行进方式:n位加法器,X与Y逐位相加,位间进位串行传送
- 串行进位加法器速度慢的主要原因是进位按串行方式传递,高位进位依赖低位进位
2、并行进位加法器
- 更多位数的CLA部件(先行进位部件)只会增加逻辑门的输入端个数,而不会增加门的级数
- 当位数较多时,全先行进位方式不太现实
- 为了进一步提高加法器的运算速度,可以进一步采用组内和组间都并行的进位方式
- 计算机内部大多采用两级或多级先行进位加法器
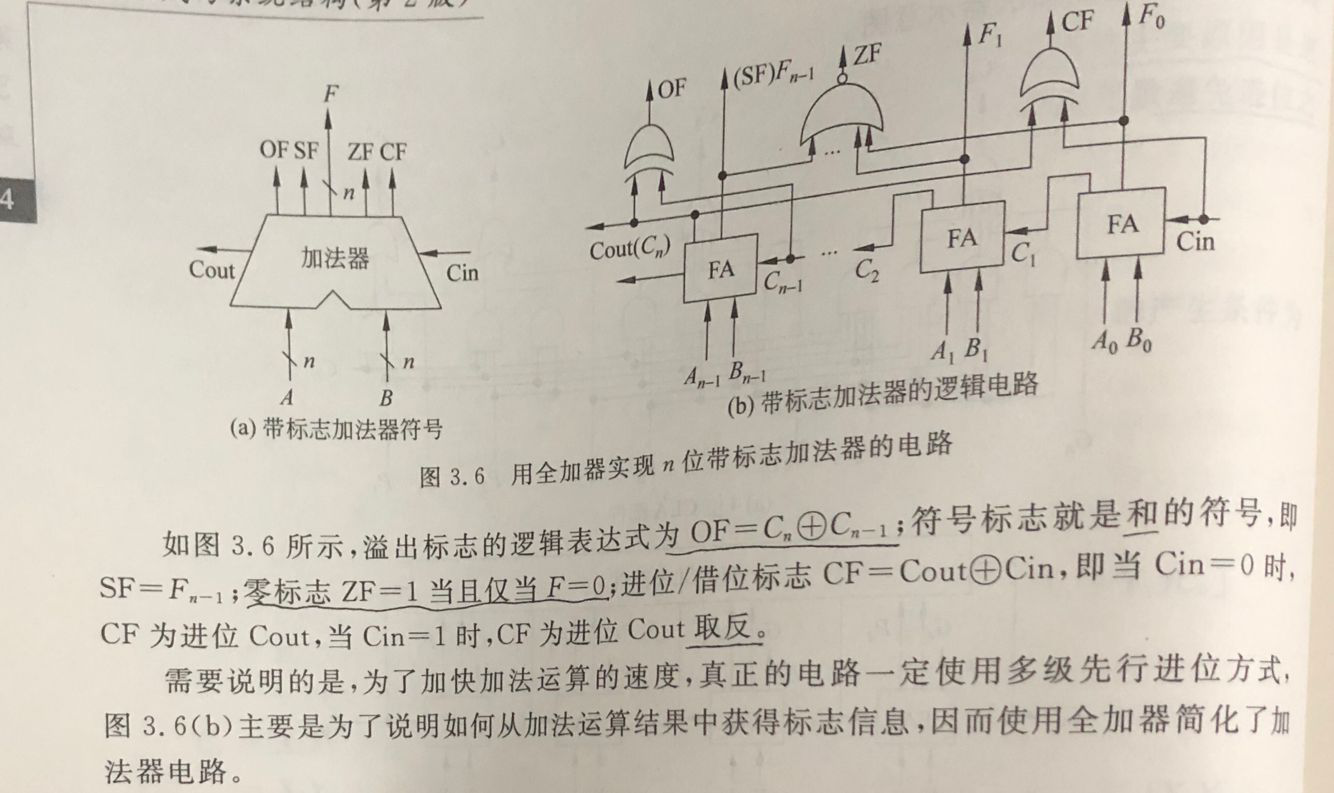
3、带标志加法器
4、算术逻辑部件
- ALU是一种能进行多种算术运算与逻辑运算的组合逻辑电路,其核心部件是带标志加法器,多采用先行进位方式
- 桶行移位器利用大量多路选择器来实现数据的快速移位,移位操作能够一次完成
- 在ALU外单独设置桶行移位器,可简化ALU的控制逻辑,并实现移位操作和ALU操作的并行性
三、定点数运算
1、补码加减运算
- [x+y]补=[x]补+[y]补(mod 2^n)
- [x-y]补=[x]补+[y]补(mod 2^n)

2、原码加减运算
- 比较两个操作数的符号,对加法实行“同号求和,异号求差”,对减法实行“异号求和,同号求差”
- 求和时,数值位相加,若最高位产生进位则结果溢出
- 求差时,被加数数值位加上加数数值位的补码
3、移码加减运算
- 移码的和、差等于和、差的补码
4、原码乘法运算
原码一位乘法
- 确定乘积的符号位,由两个乘数的符号异或得到
- 计算乘积的数值位,乘积的数值部分为两个乘数的数值部分之积
原码二位乘法
- 原码二位乘法:对乘数的每两位取值情况进行判断,使每步求出对应于该两位的部分积,则可将乘法速度提高一倍
5、补码乘法运算
补码一位乘法
- 布斯乘法:将符号位和数值位合在一起参与运算,直接得出用补码表示的乘积,且正数和负数同等对待
- 补码乘法运算规则:
(1)乘数最低位增加一位辅助位Y(-1)=0
(2)根据Y(i) Y(i-1)的值,决定是“+[x]补”、“-[x]补”还是“+0”
(3)每次加减后,算术右移一位,得到部分积
(4)重复(2)(3)步n次,结果得[xy]补 - 布斯乘法的运算过程为n次“判断-加减-右移”循环,遇到连续的1或连续的0时,可跳过加法运算直接进行右移操作
补码两位乘法
- [P(i+2)]补 = 2^(-2) ([P(i)]补 + (Y(i-1) + Y(i) - 2Y(i+1)) [x]补)
6、快速乘法器
- 阵列乘法器基于移位和求和运算,每一行被乘数与乘数中的某一位相乘,产生一组部分积
- 阵列乘法器结构规范,标准化程度高,但至少要做O(N)次加法,速度较慢
- 为提高乘法运算速度,部分积求和电路可采用树状结构,树状结构可减少求和级数
7、原码除法运算
- 当被除数和除数都不为0,并且商也不可能溢出时,才能进一步进行除法运算
- 原码除法运算与原码乘法运算一样,要将符号位和数值位分开来处理,商的符号为相除两数符号的“异或”值,商的数值为两数绝对值之商
- 单精度除法,其商的位数一定不会超过n位,因此不会发生溢出;双精度除法,商的位数可能多于n位,因此,可能发生溢出
- 计算机中两个无符号数除法的运算步骤:
(1)操作数预置
(2)做减法试商
(3)上商为0时恢复余数
(4)中间余数左移,以便继续试商
恢复余数除法
- 当中间余数和除数相减结果为负时,要多做一次+Y操作,因而降低了算法执行速度
不恢复余数除法
- “正、1、减、负、0、加”:若中间余数为正数,则上商为1,下次做减法;若中间余数为负数,则上商为0,下次做加法
8、补码除法运算
- 对于两个n位补码除法,被除数需要进行符号扩展;若被除数为2n位,除数为n位,则被除数无须扩展
- 当被除数(中间余数)与除数同号时做减法,异号时做加法
补码恢复余数除法
- 进行置商时,采用“够减则上商为1,不够减则上商为0”的上商方式,因此,最后若商为负值,则需要“各位取反,末位加1”来得到真正的商
补码不恢复余数除法
- “同、1、减、异、0、加”
四、浮点数运算
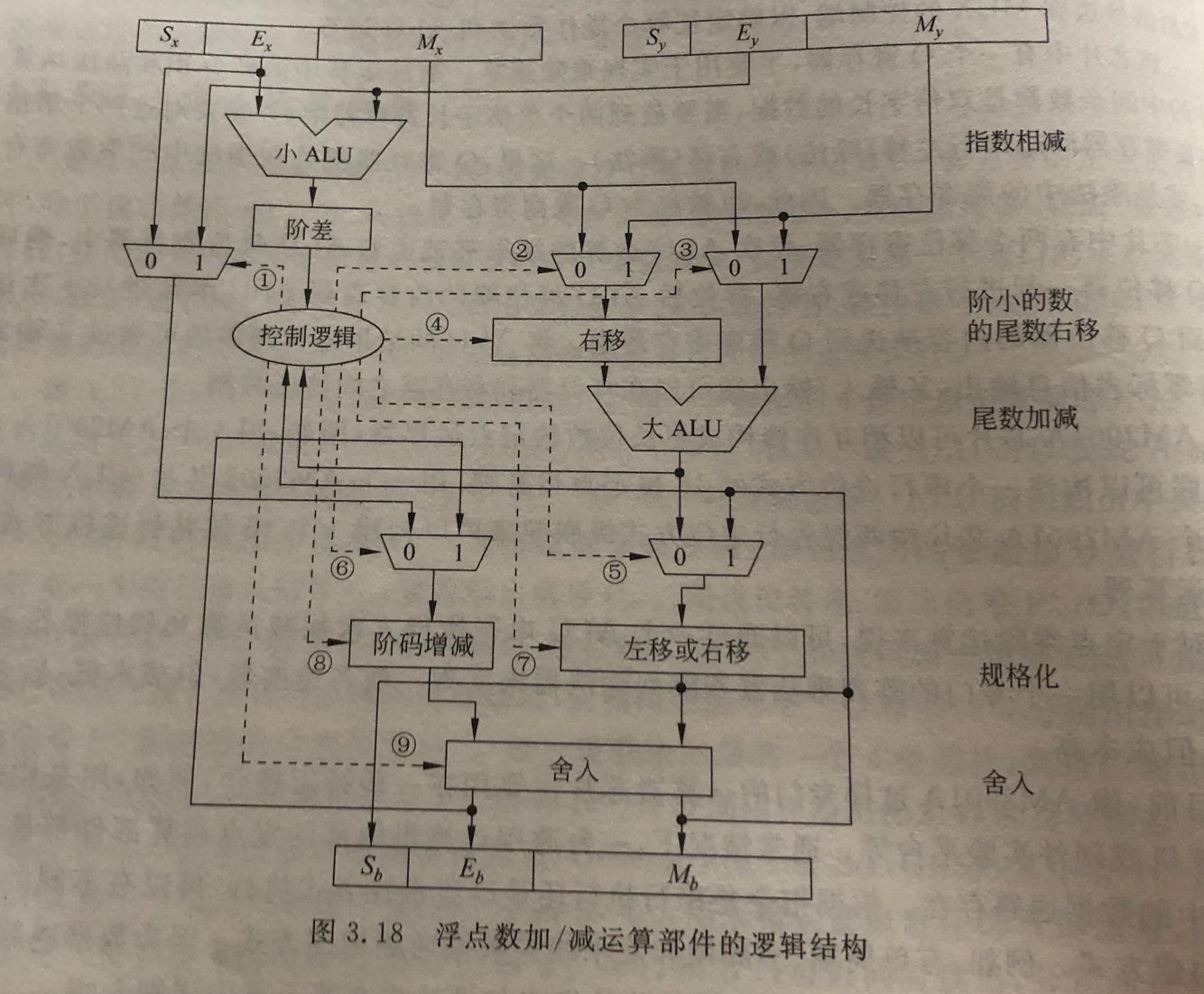
1、浮点数加减运算
对阶
- 对阶的目的:是使x和y的阶码相等,以使尾数可以相加减
- 对阶的原则是:小阶向大阶看齐,阶小的那个数尾数右移,右移的位数等于两个阶(指数)的差的绝对值

尾数加减
- 尾数加减实际上是定点原码小数的加减运算,运算过程中,在尾数右移时保留的附加位也要参加运算
- 进行加减运算后的尾数不一定是规格化的
尾数规格化
- 右规:尾数右移一位,阶码加1
- 左规:数值位逐次左移,阶码逐次减1,直到将第一位1移到小数点左边
尾数的舍入处理
- IEEE754最终对保留的附加位进行舍入的模式
(1)就近舍入(舍入为最近可表示的数)
(2)朝正无穷方向舍入
(3)朝负无穷方向舍入
(4)朝0方向舍入
溢出判断
- 浮点数的溢出并不以尾数溢出来判断,尾数溢出可以通过右规操作得到纠正
- 运算结果是否溢出主要看结果的指数是否发生了上溢,因此是由指数上溢来判断的
2、浮点数乘除运算
- 先对参加运算的操作数进行判0处理、规格化操作和溢出判断,确定参加运算的两个操作数是正常的规格化浮点数
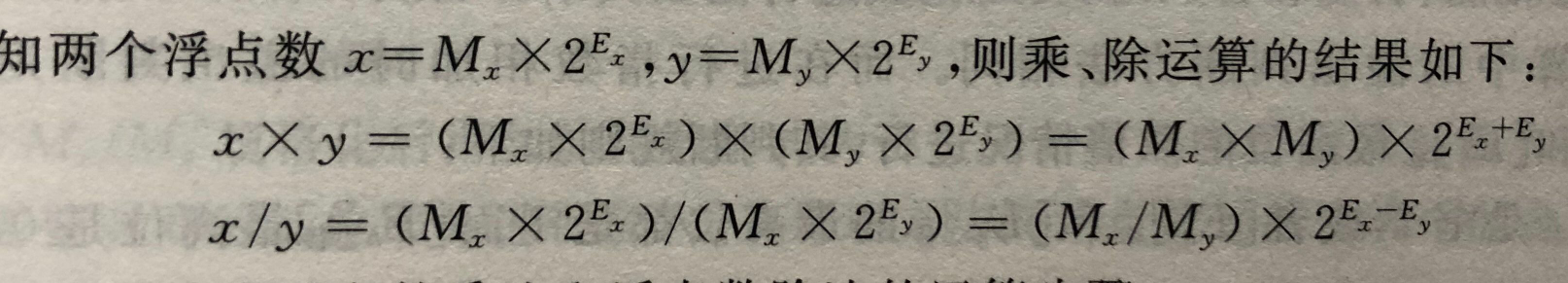
浮点数乘法运算
- 尾数相乘,指数相加;尾数规格化;尾数舍入处理;溢出判断
浮点数除法运算
- 尾数相除,阶相减;尾数规格化;尾数舍入处理;溢出判断
五、运算部件的组成
1、定点运算部件
- 一套完整的定点运算部件,除了核心部件ALU外,还需要有通用寄存器组、多路选择器、状态(标志)寄存器、移位器和用来传送数据的数据总线等