一.基本概念
1.无监督学习:数据无标签或者说是未知的,目标是通过对无标记数据的学习来揭示数据的内在性质和规律。主要研究方向有聚类,主要方法有降维
二.聚类
1.聚类:将数据样本划分为若干个通常是不相交的子集,这样每个子集就是一簇或者说是一类,每一类代表类中数据的某些规律,而且这个规律不在其他类中适用,类名由使用者来定义
2.目标:把无标签数据集分为若干类,同一簇的样本尽可能相似,不同簇的样本尽可能不同,簇之间的距离用中心点(平均)之间的距离来表示,簇之间最短距离用簇间最短样本距离来表示
3.聚类和分类:聚类是把所有无标签数据分类,类名(标签)和类的数量是自定义的,分类是模型学习标签数据的特点,从而对未知数据预测标签
三.聚类算法
(1)划分方法:k均值(k-means)


【1】初始化的聚类中心可能导致不好的局部最优:多次随机初始化选取其中代价最小的
【2】选择聚类数量:观察可视化图手动设置
【3】肘部法则:随着聚类数量的增大,损失函数也会降低,选择曲线拐点,但有时候拐点不容易看出,可以根据目的来决定聚类数量
(2)层次方法:对数据集进行层次似的分解,知道满足某个条件为止
【1】自底向上:初始每个数据样本都为一簇,通过合并相似簇来缩减类的数量
【2】自顶向下:初始所有数据为一类,通过分割最不相似的样本来增加类的数量
(3)基于密度:基于密度而不是距离,因为距离算法其实是类圆形的类划分,而基于密度则是某个区域中的密度大于某个值,就把它加到与之相似的聚类中
(4)基于模型:给每个类假定一种模型,寻找能够满足这个模型的数据
四.距离度量和相似度度量
1.两者同异
(1)同:都能表现两个样本的相似性,两个样本之间的距离越小,相似度越大,则两个样本越相似
(2)异:距离是指两个样本在空间中的距离,相似度是指两个样本的相似程度,所有距离都能在一定程度上表现相似性,不是所有相似性度量都是距离
2.距离度量
(1)p范数(闵可夫斯基距离):各个维度距离的p次方后求和再开p次方。涉及到量纲影响的时候要注意:不同维度相同距离并不表示两者一样
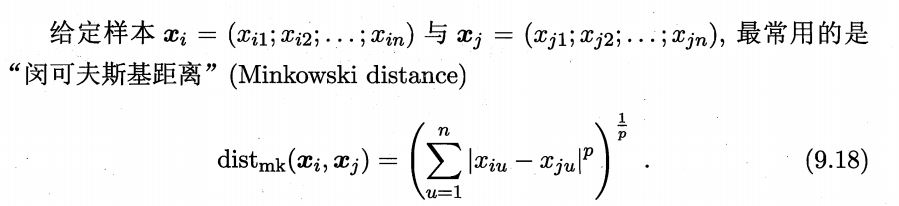
(2)曼哈顿距离(L1范数)

(3)L2范数(欧式距离)(欧几里得距离)

(4)无穷范数(切比雪夫距离)
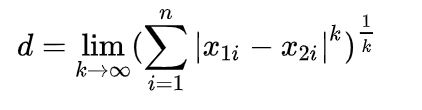
3.相似度度量
(1)余弦相似度(向量内积的变换):适合高维度向量之间的相似度计算,主要衡量的是向量方向的差异
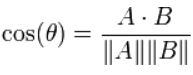
(2)Tonimoto系数:余弦相似度的改进,不仅考虑了两个向量的方向,还考虑了长度差异
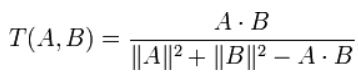
(3)皮尔逊相关系数(Pearson Correlation):用于度量两个正太分布的随机变量之间的线性相关程度,取值为[-1,1],绝对值越大,相关性越高,正数表示正相关,负数表示负相关
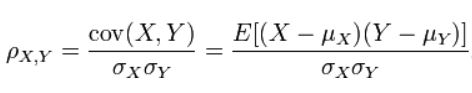
(4)Jaccard相似系数:用于比较有限样本集合之间的相似性,
