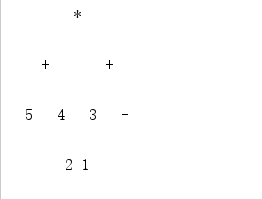20172332 2017-2018-2 《程序设计与数据结构》第六周学习总结
教材学习内容总结
第十章 树
- 1.非线性结构:树。(由结点和边的集构成)
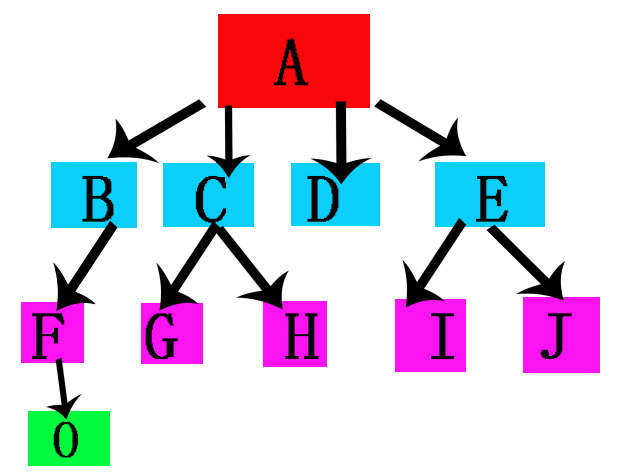
- 2.元素被存储在树的结点中,边将每个结点连接起来。每个结点都位于该树层次结构中的某一特定层上。
- 3.树的根是该树顶层的唯一结点,一棵树只有一个根。
- 4.基本的树的知识。根不是内部结点。
- 5.这里的树与实际的树是上下颠倒的,树的根是进入点,根是树中所有结点的最终祖先,沿着起始自某一特定结点的路径可以到达的结点是该结点的子孙。
- 6.结点的层就是从根结点到该结点的路径长度,从根到该结点所必须越过的边数目就可以确定其路径长度。根位于层0,根的孩子位于层1,依次类推。
- 7.树的高度是指根到叶子之间最远路径的长度。例如上图从A(根)到F(最远的叶子)的路径长度为2,所以高度为2。
- 8.树的分类方式中最重要的一条标准是树中任一结点可以具有的最大孩子数目(被称作度)。①广义树:对结点所含有的孩子数目无限制的树。②n元树:每一结点限制为不超过n个孩子的树。
- 9.二叉树:结点最多具有两个孩子的树(包括没有孩子和一个孩子的情况)。
- 10.树的所有叶子都位于同一层或者至少是彼此相差不超过一个层,就称之为是平衡。上图的F,G,H,I,J位于同一层,与D只相差一层,所以上图的树是平衡的。下图的树因为O与D相差了两层超过一层,所以这个树是不平衡的。
- 11.满树:如果一棵n元树的所有叶子都位于同一层且每一结点要么是一片叶子要么正好具有n个孩子,则称此树是满的。如图:
- 12.用链式结构实现树,每一个结点都可以定义成一个TreeNode类,每一结点都将包含一个指针,它指向将要存储在该结点的元素,以及该结点所有可能孩子的指针,也可以在每一结点中存储指向其双亲的指针。
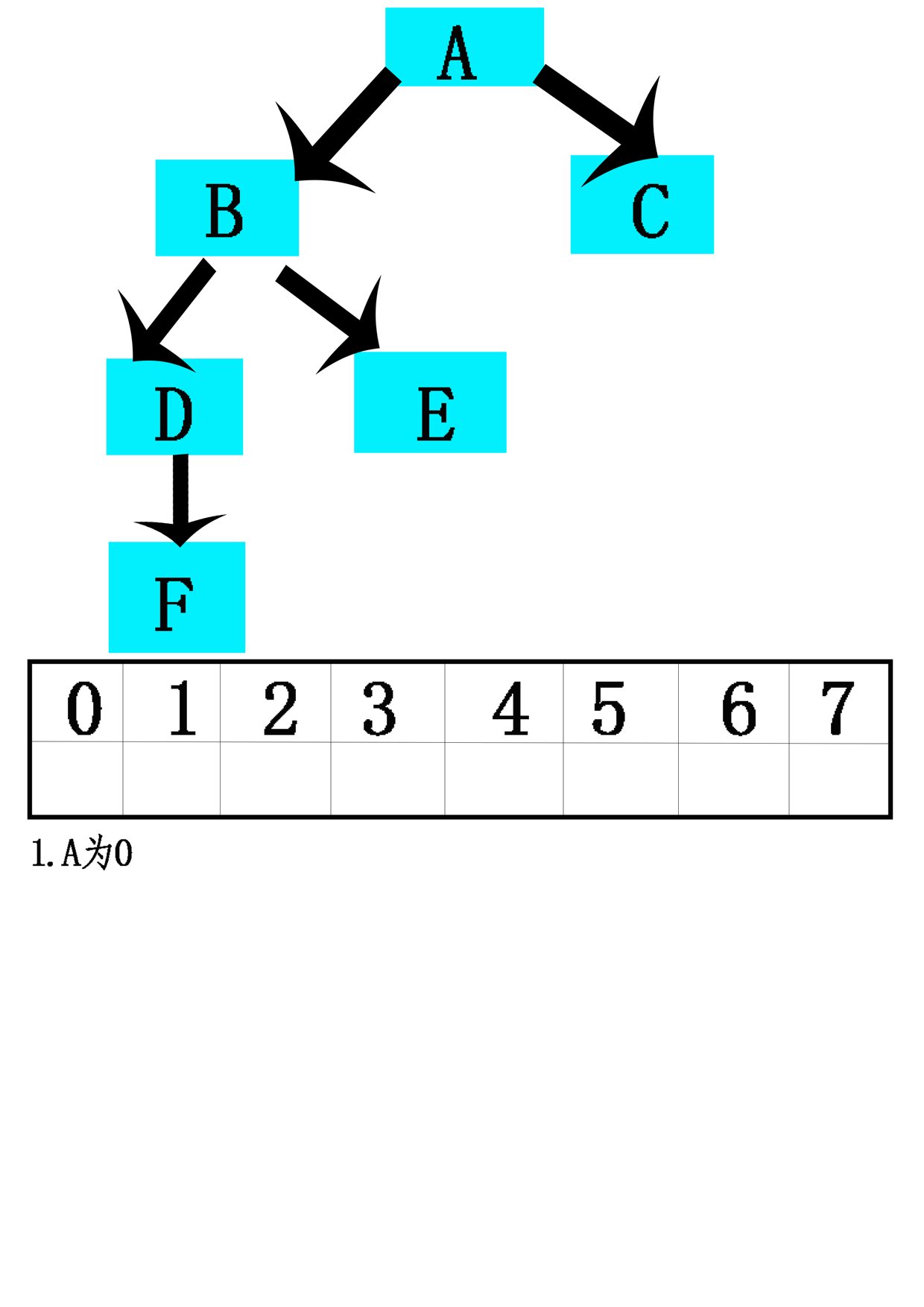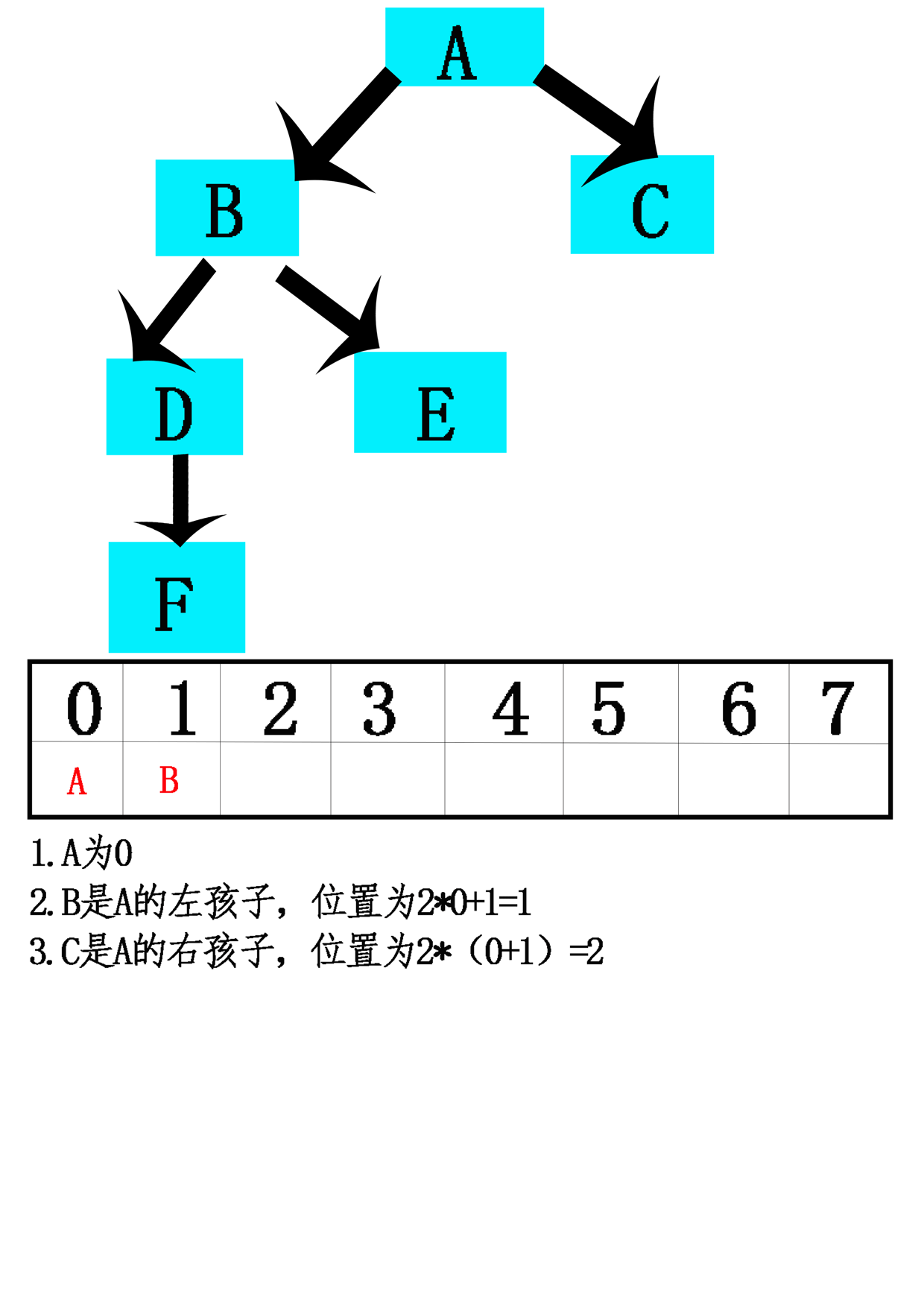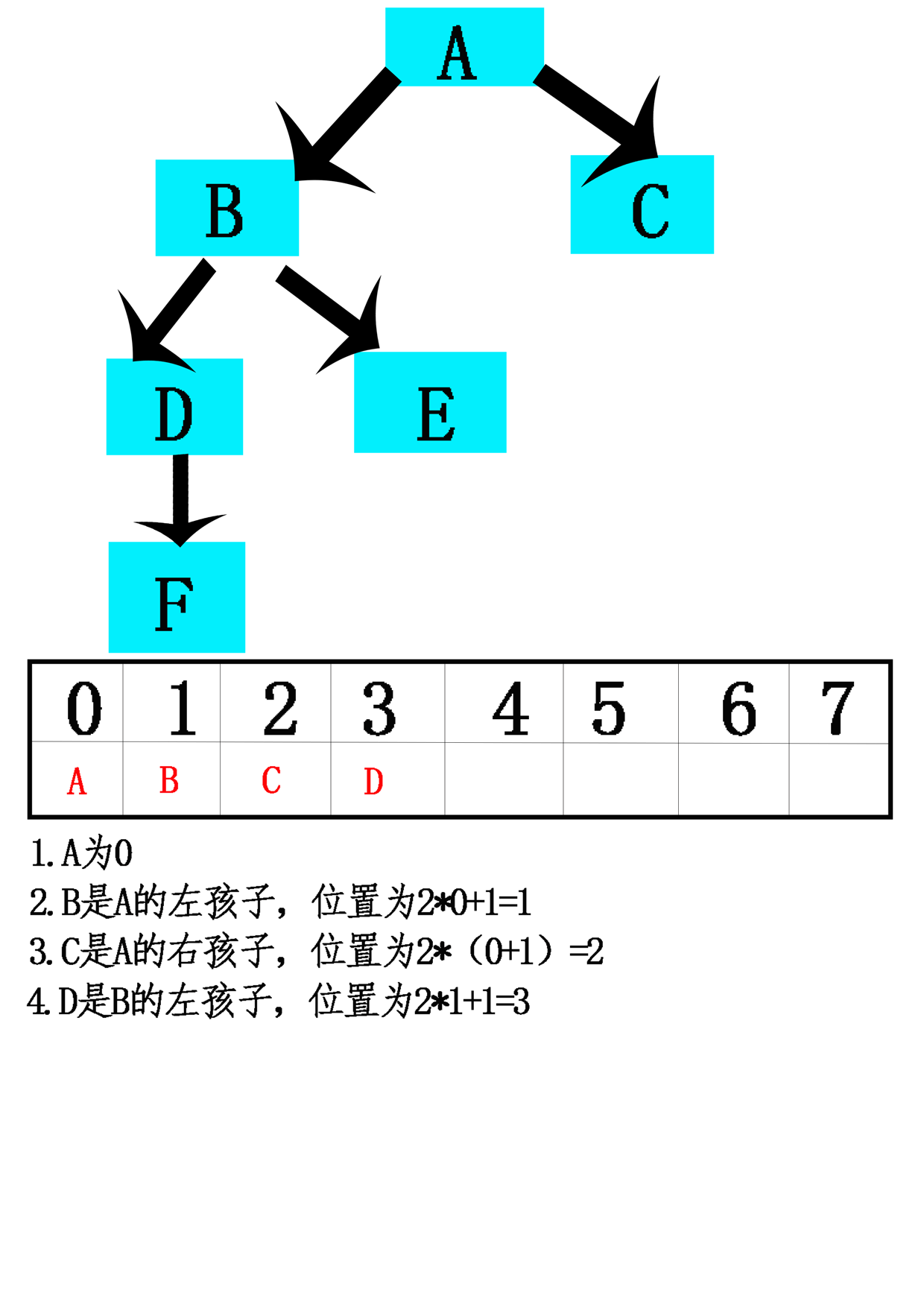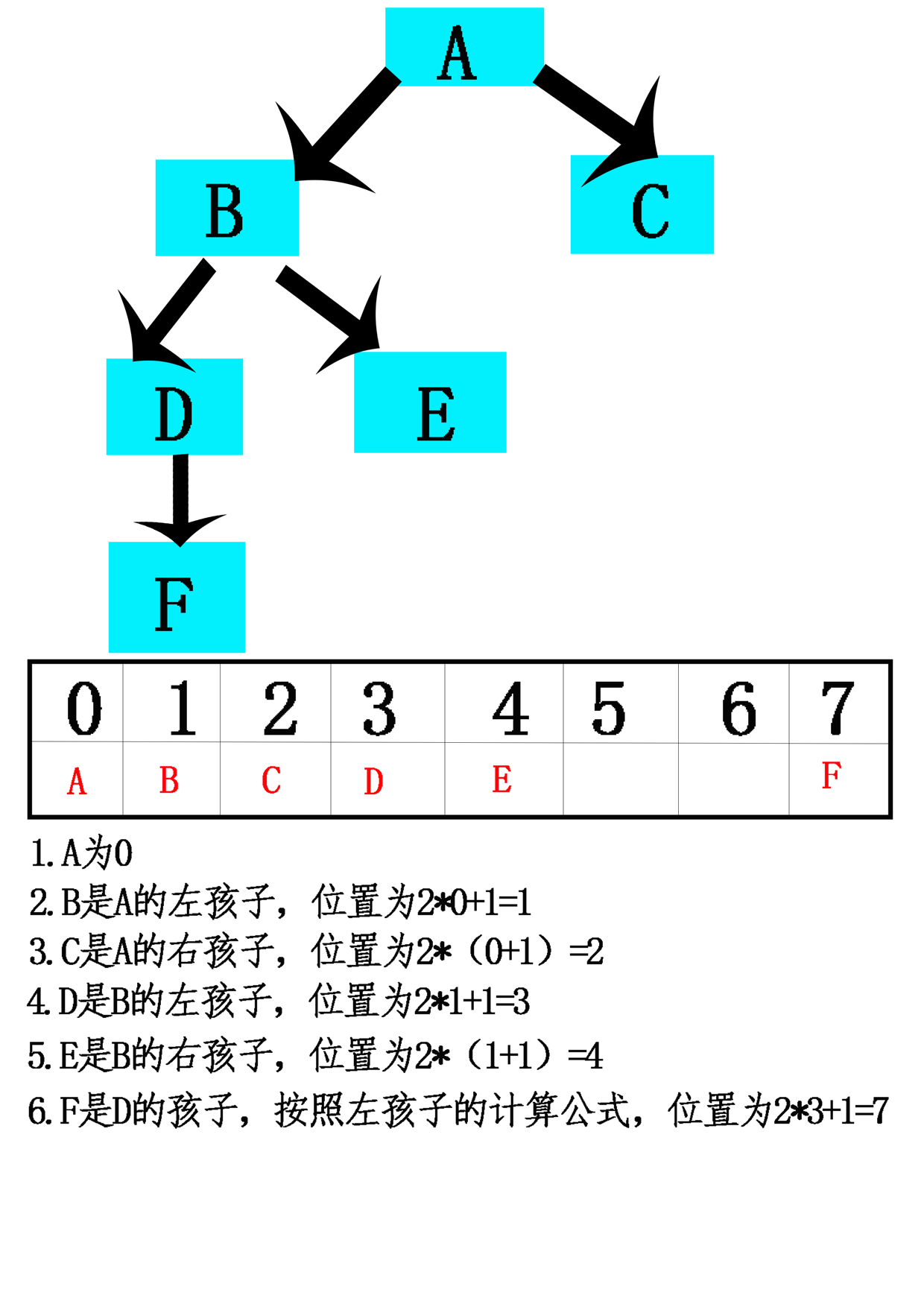
- 13.用数组实现树有两个原则方法:计算策略和模拟链接策略。
- 14.计算策略:特别是二叉树,一种策略是使用数组来存储一棵树。
- 15.模拟链接:按照先来先服务的基准连续分配数组位置,而不是通过其在树中的定位将树元素指派到数组位置上。每一结点存储的将是每一孩子(可能还有其双亲)的数组索引,而不是作为指向其孩子(可能还有其双亲)指针的对象引用变量。【不用考虑树的完全性】
- 16.模拟链接使元素能够连续存储在数组中,不会浪费空间,但是增加了删除树中元素的成本,需要进行移位操作,要么需要保留一个空闲列表。
- 17.一般而言,一棵含有m个元素的平衡n元树具有的高度为logn m。
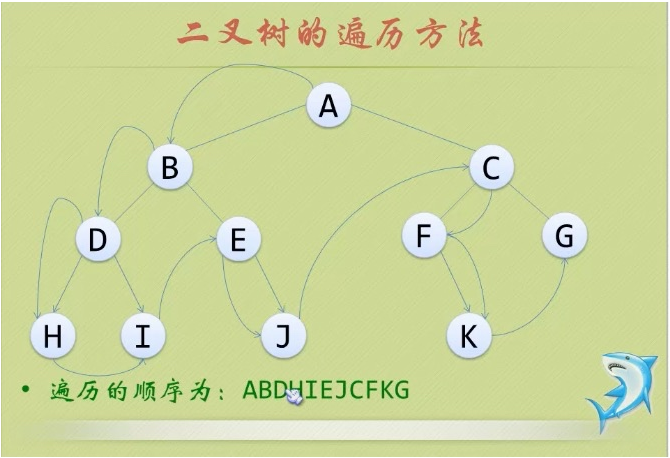
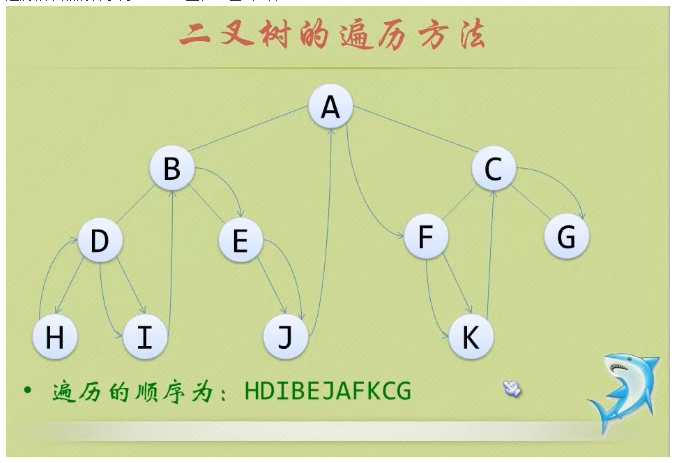
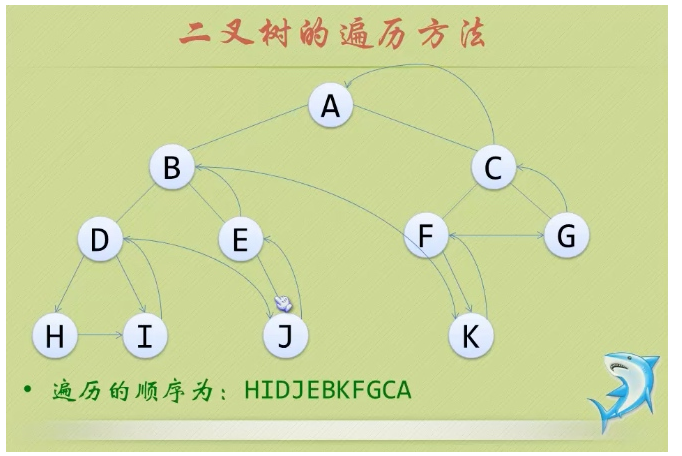
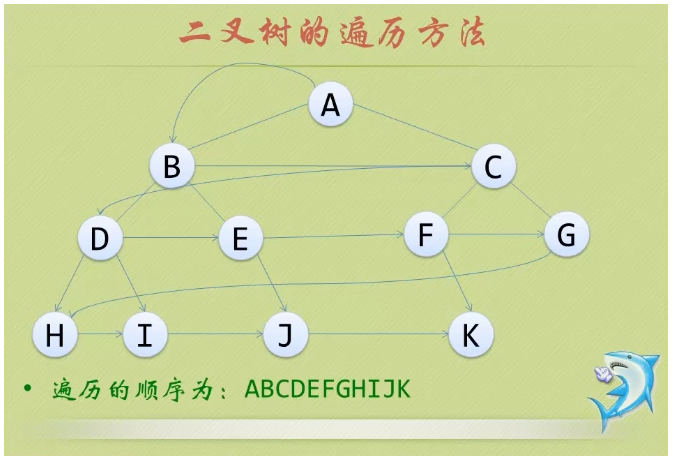
- 18.树的遍历:
- ①前序遍历:从根结点开始,访问每一结点及其孩子。
- ②中序遍历:从根结点开始,访问结点的左孩子,然后是该结点,再然后是任何剩余结点。
- ③后序遍历:从根结点开始,访问结点的孩子,然后是该结点。
- ④层序遍历:从根结点开始,访问每一层的所有结点,一次一层。
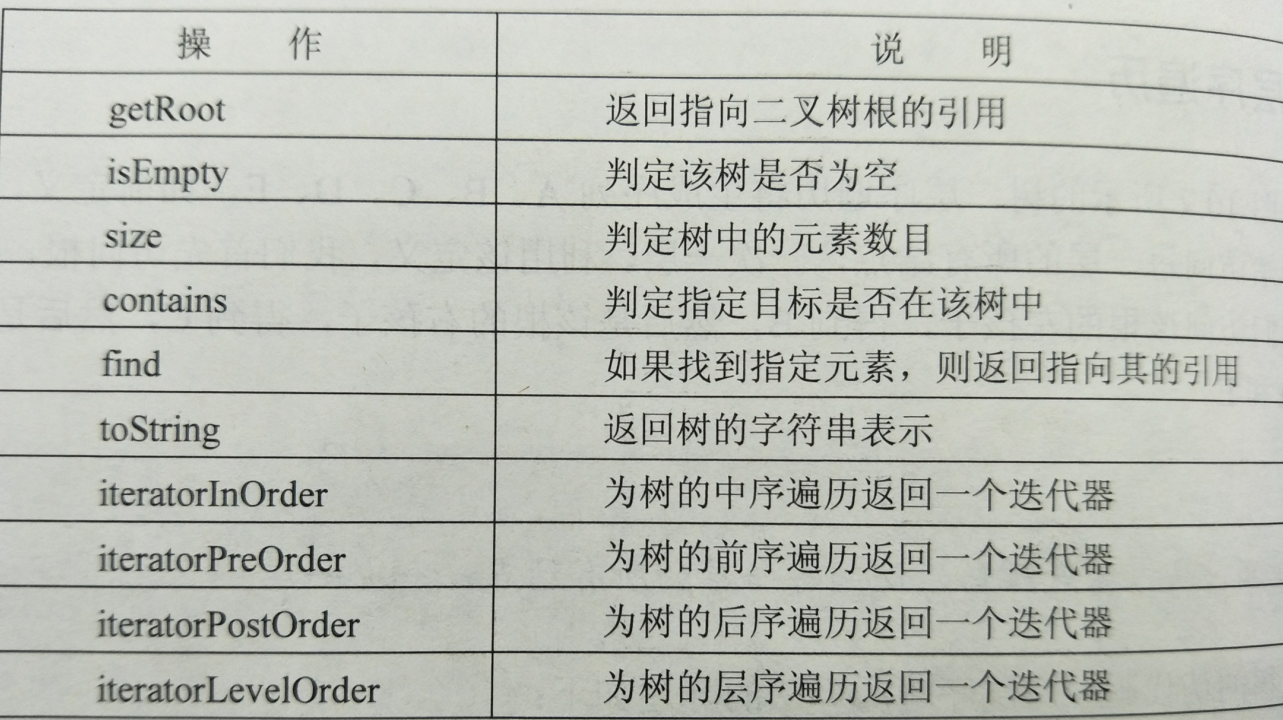
- 19.树的操作及说明:
-
20.二叉树的性质:
- (1)在二叉树的第i层上至多有2的(i-1)次方个结点。(i>=1)
- (2)深度为k的二叉树上至多含有2的k次方-1个结点(k>=1)
- (3)对任何一棵二叉树,若它含有与n0个叶子结点,n2个度为2的结点,则有n0=n2+1(分支数等于结点数-1)
-
21.完全二叉树的性质:
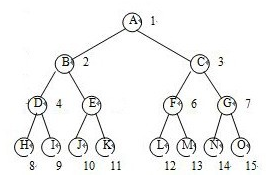
- (1)具有n个结点的完全二叉树的高度为[log2 n]+1
- (2)如果将一颗有n个结点的完全二叉树自顶向下,同一层自左向右连续给节点编号1,2,3...,则对于任意结点i(1<=i<=n),
- ①若i=1,则该i结点是树根,他无双亲。②若2i>n,则编号为i的结点无左孩子,否则他的左孩子是编号为2i的结点。③若2i+1>n,则编号为i的结点无右孩子,否则其右孩子结点编号为2i+1。
-
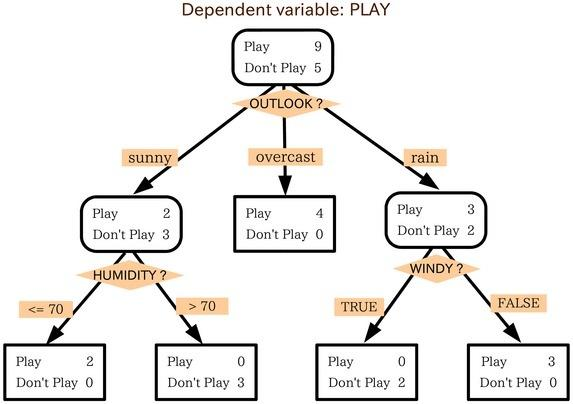
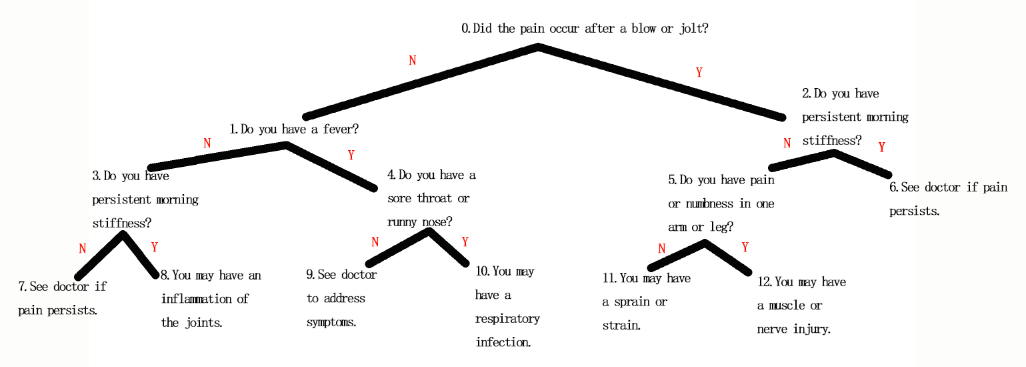
22.决策树:结点表示决策点(也就是进行判断的条件),左子结点表示“否”,右子结点表示“是”。
- 23.已知两个序列(必须有一个中序),能确定唯一树。方法:
- ①已知中序和后序。后序最后一个为根,中序根的左边为左子树,右边为右子树,再看后序,找出左边与右边,最后的又为根,以此类推。(后序定根中序分左右。)
- ②已知中序和先序。先序第一个为根,中序与上面一条一样,再看先序,找出左边与右边,第一个又为根,以此类推。(先序定根中序分左右。)
教材学习中的问题和解决过程
-
问题1:一种可能的计算策略,任何存储在数组位置n处的元素而言,左孩子和右孩子的位置有计算公式,如果只有一个孩子,位置怎么确定?
-
问题1解决方案:按照左孩子的计算公式算就可以,实际上它的位置相当于满树时所在的位置。
-
问题2:树的完全性是什么?
-
问题2解决方案:完全树从根结点到倒数第二层满足满树,最后一层可以不完全填充,其叶子结点都靠左对齐。满树一定是一棵完全树。如下图:
- 问题3:对于树的四种遍历方法的通俗理解及代码实现。
- 问题3解决方案:二叉树的前序、中序、后序遍历,就可以分成左右两支看,先按照规律走左支,走到最高层的叶子或回到根结点时,再按照同样的规律走右支。
- ①前序:遍历过程:根结点——左结点(没有左结点时输出右结点)——右结点(然后返回上一个结点找上一个结点的右孩子如没有再向上找上上个结点的右孩子。)
public void preOrder(BinaryTreeNode<T> root) {
if (root != null) {
System.out.print(root.element + " ");
preOrder(root.left);
preOrder(root.right);
}
}
- ②中序:遍历过程:先找到层数最高的左孩子——该孩子的双亲——这个左孩子的兄弟(右结点)——然后再向低一层的层数也就是该孩子的爷爷。按照定义,会发现这个爷爷的左结点已经输出过了,该结点也输出过了,所以输出该孩子的右结点,依次类推。
public void inOrder(BinaryTreeNode<T> root) {
if (root != null) {
inOrder(root.left);
System.out.print(root.element + " ");
inOrder(root.right);
}
}
- ③后序:遍历过程:先找到层数最高的左孩子——这个左孩子的兄弟(右结点)——这两个结点的双亲。按照定义,这个双亲也会有兄弟,所以再输出这个双亲的兄弟,在输出他们的双亲,以此类推。
public void postOrder(BinaryTreeNode<T> root) {
if (root != null) {
postOrder(root.left);
postOrder(root.right);
System.out.print(root.element + " ");
}
}
- ④层序:遍历过程:一层一层从根结点开始自左向右的输出。
public void levekOrder() {
if (root != null) {
LinkedList<BinaryTreeNode> queue = new LinkedList<>();
BinaryTreeNode<T> p;
queue.push(root);
while (!queue.isEmpty()) {
p = queue.removeFirst();
System.out.print(p.element + " ");
if (p.left != null)
queue.addLast(p.left);
if (p.right != null)
queue.addLast(p.right);
}
} else
System.out.println("null");
}
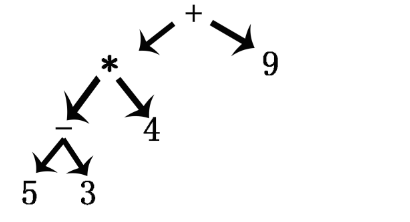
- 问题4:表达式树的计算过程是什么?
- 问题4解决方案:
- 表达式树的求值是从下往上的,对本树的分析过程,先是5-3=2,再是2*4=8,然后8+9=17
- 对于上图这种左右支都有很多孩子的树,计算过程:从层数最高的开始求,2-1=1,3+1=4,先把4放在根的右孩子上,再算左支,5+4=9,然后根的左右孩子相乘,4*9=36
- 总结:①从下往上计算;②左右两支分开计算;③四则运算前面的数都是左孩子,后面的数都是右孩子。
- 问题5:树的高度和深度区别是什么?
- 问题5解决方案:最深的叶结点的深度就是树的深度;树根的高度就是树的高度。同结点的,深度数=高度数+1。
代码调试中的问题和解决过程
- 问题1:BinaryTreeNode类中此方法的代码解读。
-
问题1解决方案:此方法运用了递归原理,判断左孩子是否存在,只要存在就+1,最后得出左孩子的总数用children变量存储。之后再算右孩子的数量,同样运用递归原理,判断右孩子是否存在,存在就+1,最后与左孩子的总数加起来,成为所有孩子(也就是没有根结点)的数量。
-
问题2:显示出树的形式的代码理解。
-
问题2解决方案:总体思想有点类似于层序输出,从根开始从右往左依次分层输出。但是需要在输出结点的同时,需要记录本层每个结点对应下一层的孩子数
public String printTree()
{
UnorderedListADT<BinaryTreeNode<ExpressionTreeOp>> nodes =
new ArrayUnorderedList<BinaryTreeNode<ExpressionTreeOp>>();
UnorderedListADT<Integer> levelList =
new ArrayUnorderedList<Integer>();
BinaryTreeNode<ExpressionTreeOp> current;
String result = "";
int printDepth = this.getHeight();
int possibleNodes = (int)Math.pow(2, printDepth +1);
int countNodes = 0;
nodes.addToRear(root);
Integer currentLevel = 0;
Integer previousLevel = -1;
levelList.addToRear(currentLevel);
while (countNodes < possibleNodes)
{
countNodes = countNodes + 1;
current = nodes.removeFirst();
currentLevel = levelList.removeFirst();
if (currentLevel > previousLevel)
{
result = result + "
";
previousLevel = currentLevel;
for (int j = 0; j < ((Math.pow(2, (printDepth - currentLevel))) - 1); j++)
result = result + " ";
}
else
{
for (int i = 0; i < ((Math.pow(2, (printDepth - currentLevel + 1)) - 1)) ; i++)
{
result = result + " ";
}
}
if (current != null)
{
result = result + (current.getElement()).toString();
nodes.addToRear(current.getLeft());
levelList.addToRear(currentLevel + 1);
nodes.addToRear(current.getRight());
levelList.addToRear(currentLevel + 1);
}
else {
nodes.addToRear(null);
levelList.addToRear(currentLevel + 1);
nodes.addToRear(null);
levelList.addToRear(currentLevel + 1);
result = result + " ";
}
}
return result;
}
- 代码理解:因为这段代码很长,不懂的地方很多,所以一段一段的分析。
- ①printDepth显而易见是得到这棵树的高度(根结点所在层为0),根据二叉树的性质(2)深度为k的二叉树上至多含有2的k次方-1个结点(k>=1)因为我的
getHeight()是高度,所以可以知道possibleNodes(最多结点数为)2的^(printDepth+1)-1
int printDepth = this.getHeight();
int possibleNodes = (int)Math.pow(2, printDepth +1);
- ②currentLevel表示输出结点的下一层的孩子数,previousLevel表示当前层数的孩子数分配,因为刚开始根为0,所以需要等于-1。在循环中,把数据从根依次放进名为nodes无序列表的前端,levelList的无序列表记录下一次的孩子数的分配
nodes.addToRear(root);
Integer currentLevel = 0
Integer previousLevel = -1;
levelList.addToRear(currentLevel);
- ③当前的结点数之前定义为0,比最大可能的结点数小的时候就进入循环。保证输出全部的结点。
while (countNodes < possibleNodes)
{
countNodes = countNodes + 1;
current = nodes.removeFirst();
currentLevel = levelList.removeFirst();
- 无上面代码的效果图:
- ④
result = result + " ";是因为二叉树,为了形成树的形状,所以相当于 为一组的存在,不会让数在一行,同时保证了每行第一个数之前的空格数。其中for循环的循环体为了保证每行第一个数之前的空格数。
if (currentLevel > previousLevel)
{
result = result + "
";
previousLevel = currentLevel;
for (int j = 0; j < ((Math.pow(2, (printDepth - currentLevel))) - 1); j++)
result = result + " ";
}
- 无上面代码的效果图:
- 无上面代码for循环的效果图:
- ⑤保证结点间的距离,不让每个元素紧挨在一起,分不清。
else
{
for (int i = 0; i < ((Math.pow(2, (printDepth - currentLevel + 1)) - 1)) ; i++)
{
result = result + " ";
}
}
- 无上面代码的效果图:
- ⑥输出所有的结点
if (current != null)
{
result = result + (current.getElement()).toString();
nodes.addToRear(current.getLeft());
levelList.addToRear(currentLevel + 1);
nodes.addToRear(current.getRight());
levelList.addToRear(currentLevel + 1);
}
- 无上面代码的效果图:
- ⑦为了输出左支为空,右支还有结点的情况。
else {
nodes.addToRear(null);
levelList.addToRear(currentLevel + 1);
nodes.addToRear(null);
levelList.addToRear(currentLevel + 1);
result = result + " ";
}
}
- 无上面代码的效果图:
- 问题3:背部诊断器的相关文件是存在的,但是不能运行。
-
问题3解决方案:因为文件放错位置了,默认是工程根目录,和src是同一个级别的文件。不能放在src文件中,更不能放在src文件的子文件中。
-
问题4:DecisionTree类的代码理解。
public DecisionTree(String filename) throws FileNotFoundException
{
File inputFile = new File(filename);
Scanner scan = new Scanner(inputFile);
int numberNodes = scan.nextInt();
scan.nextLine();
int root = 0, left, right;
List<LinkedBinaryTree<String>> nodes = new java.util.ArrayList<LinkedBinaryTree<String>>();
for (int i = 0; i < numberNodes; i++)
nodes.add(i,new LinkedBinaryTree<String>(scan.nextLine()));
while (scan.hasNext())
{
root = scan.nextInt();
left = scan.nextInt();
right = scan.nextInt();
scan.nextLine();
nodes.set(root, new LinkedBinaryTree<String>((nodes.get(root)).getRootElement(),
nodes.get(left), nodes.get(right)));
}
tree = nodes.get(root);
}
- 问题4解决方案:这个方法是为了把文件中的问题放入树中的结点中,让问题组成一个树(决策树),然后再用判定的方法进行判断。
- 文件内容如下图,第一个数13为结点数。
- 下图是从文件中读出的信息所组成的树。
- 关键代码及解释:
- ①为了把读入的内容变为结点。
List<LinkedBinaryTree<String>> nodes = new java.util.ArrayList<LinkedBinaryTree<String>>();
for (int i = 0; i < numberNodes; i++)
nodes.add(i,new LinkedBinaryTree<String>(scan.nextLine()));
- ②确定结点的位置,第一个数为根的位置,第二个数为左孩子的位置,第三个数为右孩子的位置,然后把相应的结点放入树中。
while (scan.hasNext())
{
root = scan.nextInt();
left = scan.nextInt();
right = scan.nextInt();
scan.nextLine();
nodes.set(root, new LinkedBinaryTree<String>((nodes.get(root)).getRootElement(),
nodes.get(left), nodes.get(right)));
}
代码托管
上周考试错题总结
- 无。
点评过的同学博客和代码
其他(感悟、思考等,可选)
- 因为是第一次学习这种非线性结构,所以刚开始的时候有点摸不着头脑,有一些较难的点,花费了自己大量的时间去学习,但是觉得很有收货。
学习进度条
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | 重要成长 | |
|---|---|---|---|---|
| 目标 | 5000行 | 30篇 | 400小时 | |
| 第一周 | 0/0 | 1/1 | 2/2 | |
| 第二周 | 1010/1010 | 1/2 | 10/12 | |
| 第三周 | 651/1661 | 1/3 | 13/25 | |
| 第四周 | 2205/3866 | 1/4 | 15/40 | |
| 第五周 | 967/4833 | 2/6 | 22/62 | |
| 第六周 | 1680/6513 | 1/7 | 34/96 |
-
计划学习时间:20小时
-
实际学习时间:34小时
-
改进情况:这周的新内容难度很大,学习时间远超自己的计划时间