神经网络学习
1、输出与输入的关系(感知基):
$$
y=\begin{Bmatrix}
1 & {\overrightarrow{x}\cdot \overrightarrow{w}+b>0}\
0 & {\overrightarrow{x}\cdot \overrightarrow{w}+b\leqslant 0}
\end{Bmatrix}
$$
这个模型由生活中而来,$\overrightarrow{x}$是输入表示各种情况,$\overrightarrow{w}$表示各种情况的影响权重,$\overrightarrow{x}\cdot \overrightarrow{w}$得到整体的影响,$b$是门限(偏移)当影响$y>0$就做出1决策,否则就做出0决策。
2、为什么要使用(sigmoid neuron):
$$
y=\frac{1}{1+e^{-(\overrightarrow{x}\cdot \overrightarrow{w}+b)}}
$$
感知基是一个不连续的函数,可能微小的改变$\Delta \overrightarrow{w}$,会导致$y$的翻转性的变化。使用sigmoid neuron,使y与w和b是连续关系(微小的$\Delta \overrightarrow{w}$,y也是微小的变化),且输出的值在0~1之间,所以选择$\frac{1}{1+e^{-x}}$
3、误差函数
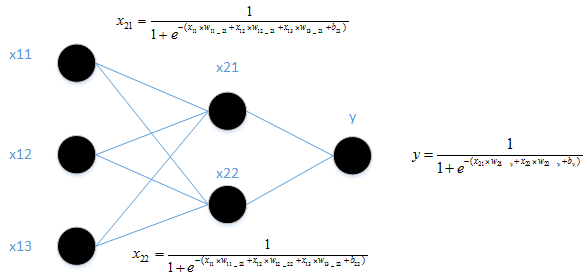
输出与输入的关系最好为如下,看起来很复杂的样子。
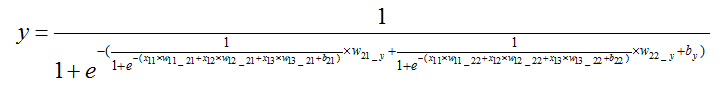
误差函数为:
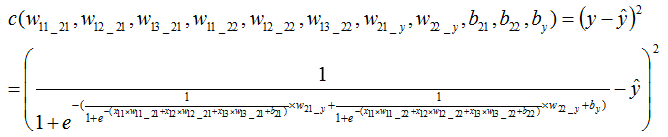
很多时候会使用一个平均误差函数,为什么我还不懂。
梯度下降法就是从导数方向调整w和b,使误差函数(代价函数)的值最小。(统计值最小,所以要求一个平均误差),其中权重和偏移b的导数如下

看起来很复杂,反向传播的方式计算起来就没那么复杂了。
导数的反方向是降低误差函数c的最快的方向,给定一个学习率$\eta$,每次学习调整$\eta\frac{\alpha }{w_{11_21}}$
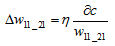
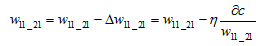
最终使c达到最小。
原文写于2019-12-05,2021-12-08改为markdown