生物信息学-基因表达分析
为了丰富中心法则,研究人员使用不断更新的技术研究lncRNA的方方面面,其中技术主要是生物学上的微阵列芯片技术和表达数据分析方法,方方面面是指lncRNA的位置特征。
Background:根据中心法则,发现DNA与RNA与protein之间的关系,此时认为找到的RNA全部用于编码protein,但是实验结果中:非编码RNA含量高,而coding区只占很少的一部分。研究非编码RNA,发现noncoding与protein expression有关,所以总思路变成了研究noncoding区从而丰富中心法则,而研究noncoding区的前提是转录组分析。
转录组研究
1.依据实际研究的问题,可以有不同的思路
时间(生长发育不同阶段)特异性
空间(身体不同区域)特异性
Normal 与否
- 随着测序技术的发展,出现了以下RNA的测序手段
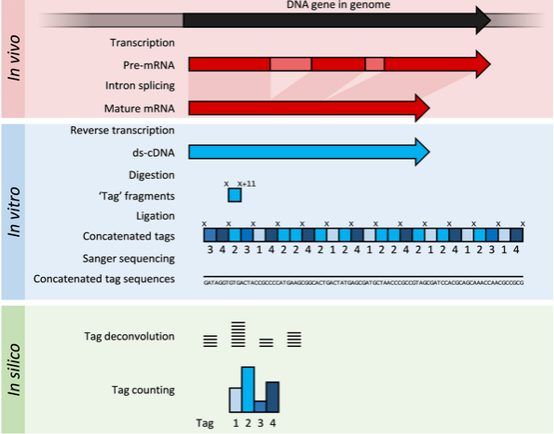
SAGE:将RNA反转录得到的cDNA打碎,利用sanger测序法得到最后的序列
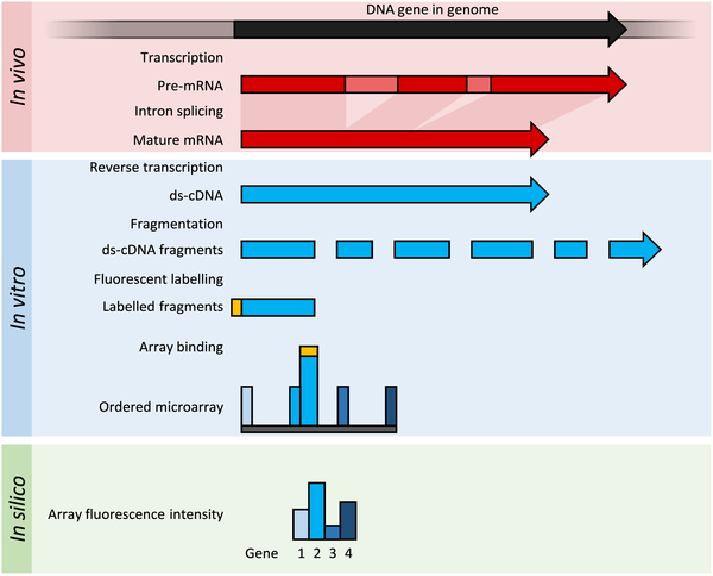
DNA微阵列: 将RNA打碎,用基于reference的探针(特指基因芯片)测得序列,此方法灵敏性高
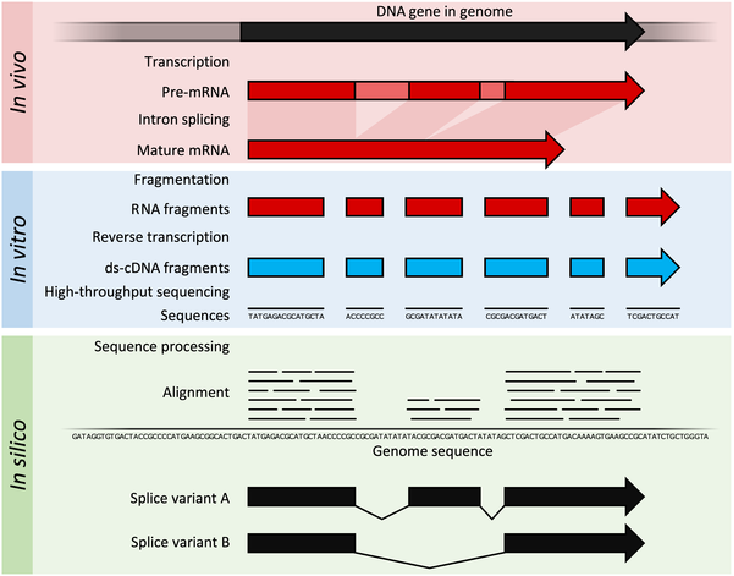
RNA-seq:将RNA打碎,再将片段RNA反转录cDNA,利用二代测序(short reads)assembly而成。
Long noncoding RNA
定义:
1.因为200bp,所以long;
2.因为No protein produce但同时有与coding gene具有相似结构(都有intro和exon),所以lncRNA长期被认为是假基因,直到发现其和转录调控有关系,才开始被重视。
起源:
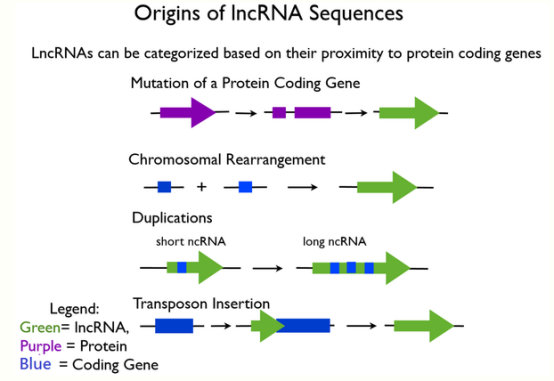
- coding gene mutation变成noncoding gene,所以无法coding protein
- Chromosome重组
- sncRNA加倍成为lncRNA
- sncRNA插入coding gene使之丧失功能但长度变长,成为lncRNA
分类:基于与protein的位置

lncRNA发现历史:
在大规模测序出现之前,只能利用sanger发现单个lncRNA。在完成human genome 之后,基于该数据库,得到的芯片,大大加速了lncRNA的发现。随着二代测序的大规模使用,大量发现结构,因此诞生了基于不同算法的assembly&annotation软件(eg,scripture、tophat、cufflinks)。所以,如今的思路是利用不同工具处理相同数据,将得到的不同结果集成为更准确的genome,从而得到比较可靠的reference。(review:Rinn and Chang,2012)但是2015用更多的原始数据用同样方法重做,发现其中有79%之前没有的,这是因为原始数据采集更在时间和空间上更为细致了。如今,得到了NONCODE (数量最多dataset)、MITranscript (最新)等各有侧重的数据库。
Assembly比对方式:
1.交叉--保留
2,存在不交叉的,利用其它参数信息(eg,位置信息)筛选
Gene expression 分析:
原则:重复&随机&间隔
Replication:biology(eg,同一个gene测100次得到100个sequence信息) &technical(对于100个sequence信息,可以随机抽取其中的任意N个,这种抽取做M次),这都是为了数据能更好的反应客观事实。
Randomization:无论是抽选或是物理设备参数设定,都要保证随机性。
Blocking:生物学实验的连贯性(物理条件一致,eg,一天一个完整实验,而不是一天所有完整实验中的一个步骤)
以微阵列方法为例的流程:
在仪器上得到荧光信号,将这些应该信号按照光的亮度赋值,由图转变为表,该表就是表达谱。根据荧光信号的特点,比如中间较强周围较弱就比较好,进行质量控制,也就是筛选质量较好的sample。此时,所有gene的表达量都在一个表格里面,其中使用三张芯片就被叫做生物学重复,以此创造:
|
|
芯片1 |
芯片2 |
芯片3 |
|
Gene1 |
2 |
4 |
4 |
|
Gene2 |
5 |
4 |
14 |
|
Gene3 |
4 |
6 |
8 |
可知芯片1比芯片3的光照程度整体普遍弱,这可能是由于物理因素造成的。为了进行比较,要将其数值进行归一化(normalization),依据比价对象的不同,可将方法分为两种:
- Intra:eg,芯片1内部比较不同gene表达量(技术是双通道的MA,归一化方法是LOWESS )
- Inter:eg,gene1在不同芯片上的表达量,(技术是单通道;思路可以是中位数归一化或qualitile归一化图
其中,qualitile归一化 的过程是:
|
|
芯片1 |
芯片2 |
芯片3 |
|
Gene1 |
2 |
4 |
4 |
|
Gene2 |
5 |
4 |
14 |
|
Gene3 |
4 |
6 |
8 |
不看属于哪个gene,在芯片内部进行排序:
|
|
芯片1 |
芯片2 |
芯片3 |
|
Mean=10/3 |
2(Gene1) |
4(Gene1) |
4(Gene1) |
|
Mean=16/3 |
4(Gene3) |
4(Gene2) |
8(Gene3) |
|
Mean=25/3 |
5(Gene2) |
6(Gene3) |
14(Gene2) |
求均值并写回去,这样做是为了避免物理错误,物理错误会导致整张芯片的效果都不好。不用考虑排序会因为表达量一致而造成误差,因为实际上不存在表达量完全一致的情况:
|
|
芯片1 |
芯片2 |
芯片3 |
|
Gene1 |
10/3 |
10/3 |
10/3 |
|
Gene2 |
25/3 |
16/3 |
25/3 |
|
Gene3 |
16/3 |
25/3 |
16/3 |
归一化之后,利用假设检验证明实际问题。
当数据服从某种分布(既有参数)时,可就某些参数(eg,mean)进行假设检验
当数据未知分布(即无参数),则采用permutation test:
使用的理论是t检验中的SAM,因为t-test需要有参数,但是现在数据未知参数,所以加入置换测试的方法
SAM"Statistical Analysis of Microarrays" specifically designed for microarray data analysis. It relies on the non-parametric permutation test. SAM is a variant of the t-test. Shown below is an excerpt of Tushner's paper describing the SAM algorithm:
Eg,分为测试组(treatment)和对照组(control):下图是它们的数据分布D
|
Key |
T1 |
T2 |
T3 |
C1 |
C2 |
C3 |
|
Gene1 |
1 |
2 |
3 |
4 |
5 |
6 |
将其随机打乱成1000个类似于下方表格的sample:
比如其中的2个是:
|
Key |
T1 |
T2 |
T3 |
C1 |
C2 |
C3 |
Mean of T |
Mean of C |
STDEV of all |
|
Gene1 |
6 |
1 |
2 |
3 |
4 |
5 |
3 |
4 |
1.870828693 |
|
Key |
T1 |
T2 |
T3 |
C1 |
C2 |
C3 |
Mean of T |
Mean of C |
STDEV of all |
|
Gene1 |
5 |
1 |
2 |
3 |
4 |
6 |
2.666666667 |
4.333333333 |
1.870828693 |
其中,S0是给定值,d可以认为是改良版的t值,如此得到1000个t值,这1000个t值可构成正态分布统计图表,最后根据总体分布,找到数据分布D的p值,而后根据该p值判断假设检验的结果。
由此,可以得到所有基因对应的p值,但是因为p值的错误率很高,所以需要采用多重假设检验对p值做检查。
可采用FDR
首先对于每个基因来说,都有p值,p值的含义是false positive rate(FPR,假正率):q值是false discovery rate (FDR):
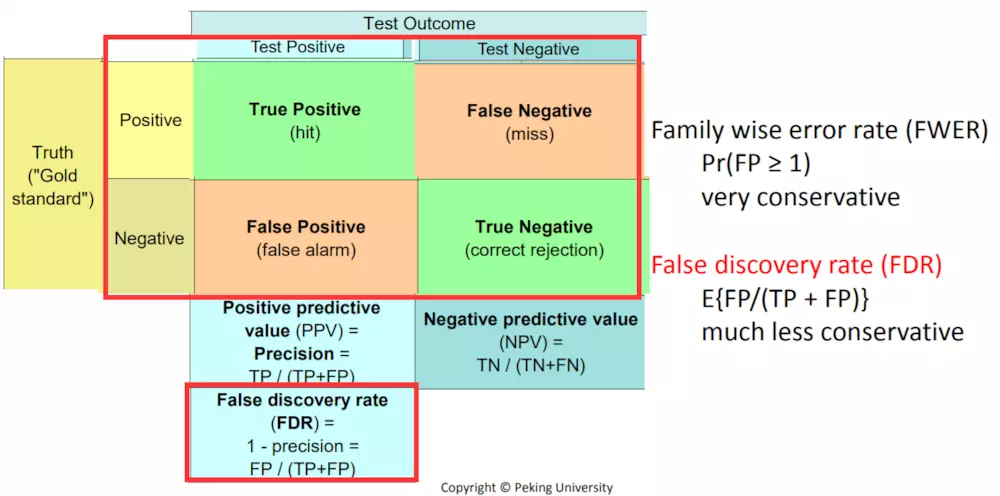
因为未知真实情况,但是从上图可知真实情况和估算情况之间的关系,所以可以使用别的方法计算FWER和FDR。
Control of FWER:
The Bonferroni procedure
Tukey's procedure
Holm's step-down procedure
Control of FDR
Benjamini–Hochberg procedure
Benjamini–Hochberg–Yekutieli procedure
例如,BH:
,
,所以q-value的期望即是FDR,所以,求出每个gene的q-value即可
原先每个gene都有自己的p值:
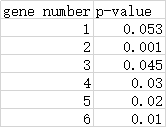
可靠gene的p值满足: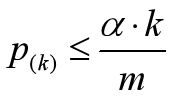
可靠gene的q值满足:
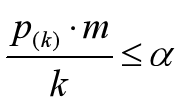
其中,k是gene number号,a是自己设定的0.05,m是所有gene个数,在这里是6;
把gene按照p值排序并据公式处理,得到:

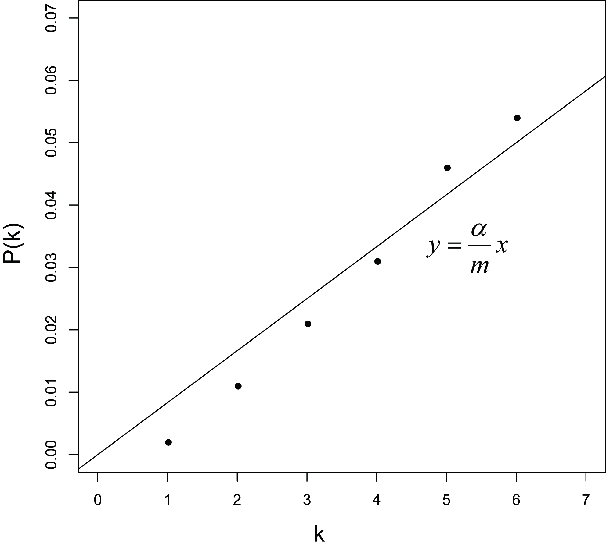
若写为函数表达则可得到上图,有四个gene的p值是可靠的。
