目录
求组合数
求组合数 I
题目
给定n组询问,每组询问给定两个整数a,b,请你输出Cba mod (1e9 + 7)的值。
输入格式
第一行包含整数n。
接下来n行,每行包含一组a和b。
输出格式
共n行,每行输出一个询问的解。
数据范围
1≤n≤10000,
1≤b≤a≤2000
输入样例:
3
3 1
5 3
2 2
输出样例:
3
10
1
思路: c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % mod
先用递推预处理一下C数组;
然后直接输出
答案
#include<bits/stdc++.h>
using namespace std;
const int N = 2010, mod = 1e9 + 7;
int c[N][N];
void init(){
for(int i = 0; i < N; i ++)
for(int j = 0; j <= i; j ++)
if(!j) c[i][j] = 1;
else c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % mod;
}
int main(){
int n;
cin >> n;
init();
while(n --){
int a, b;
scanf("%d%d" , &a, &b);
cout << c[a][b] << endl;
}
return 0;
}
求组合数 II
题目
给定n组询问,每组询问给定两个整数a,b,请你输出Cba mod (1e9 + 7)的值。
输入格式
第一行包含整数n。
接下来n行,每行包含一组a和b。
输出格式
共n行,每行输出一个询问的解。
数据范围
1≤n≤10000,
1≤b≤a≤105
输入样例:
3
3 1
5 3
2 2
输出样例:
3
10
1
思路
先预处理所有i的阶乘以及其逆元,然后用公式进行求解

i的阶乘的逆元相当于 i的阶乘的-1次方,用乘法可以保证mod的时候不会出错。
逆元的一点笔记
注意:由于数据较大,计算的时候要用到long long ,两个1e9相乘的话不会溢出,但是三个的话就可能溢出了
答案
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 100010, mod = 1e9 + 7;
int fact[N], infact[N];
int qmi(int a, int k, int p){
int res = 1;
while(k){
if(k & 1)res = (ll) res * a % p;
a = (ll) a * a % p;
k >>= 1;
}
return res;
}
int main(){
fact[0] = infact[0] = 1;
for(int i = 1; i < N; i ++){
fact[i] = (ll) fact[i - 1] * i % mod;
infact[i] = (ll)infact[i - 1] * qmi(i, mod - 2, mod) % mod;
}
int n;
cin >> n;
while(n --){
int a, b;
scanf("%d%d" , &a, &b);
printf("%d
", (ll)fact[a] * infact[b] % mod * infact[a - b] % mod);
}
return 0;
}
求组合数 III
题目
给定n组询问,每组询问给定三个整数a,b,p,其中p是质数,请你输出Cba mod p的值。
输入格式
第一行包含整数n。
接下来n行,每行包含一组a,b,p。
输出格式
共n行,每行输出一个询问的解。
数据范围
1≤n≤20,
1≤b≤a≤1018,
1≤p≤105,
输入样例:
3
5 3 7
3 1 5
6 4 13
输出样例:
3
3
2
思路:Lucas定理(卢卡斯定理)

时间复杂度: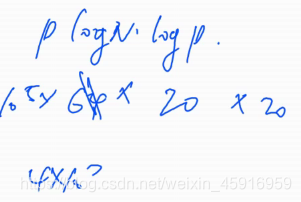
具体证明先放一旁,
不过只要 A和B 都小于p就可以用公式了。
答案
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int qmi(int a, int k, int p){
int res = 1;
while(k){
if(k & 1) res = (ll) res * a % p;
a = (ll)a * a % p;
k >>= 1;
}
return res;
}
int C(int a, int b, int p){
if(b > a) return 0;
int res = 1;
for(int i = 1, j = a; i <= b; i ++, j --){
res = (ll) res * j % p;
res = (ll) res * qmi(i, p - 2, p) % p;
}
return res;
}
int lucas(ll a, ll b, int p){
if(a < p && b < p) return C(a, b, p);
return (ll) C(a % p, b % p, p) * lucas(a / p, b / p, p) % p;//将可以取余的部分用C,然后继续除p再取余用C……
}
int main(){
int n;
cin >> n;
while(n --){
ll a, b;
int p;
cin >> a >> b >> p;
cout << lucas(a, b, p) << endl;
}
return 0;
}
求组合数 IV
题目
输入a,b,求Cba的值。
注意结果可能很大,需要使用高精度计算。
输入格式
共一行,包含两个整数a和b。
输出格式
共一行,输出Cba的值。
数据范围
1≤b≤a≤5000
输入样例:
5 3
输出样例:
10
思路
因为Cnm全是乘法嘛,就可以:
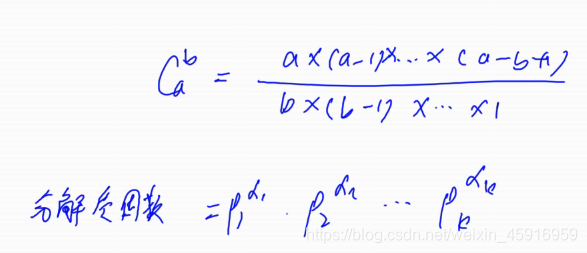
第一步:分解质因数
第二步:高精度乘法
先看分子里面有多少个p,再把分母里面的p的个数减去,就是p的个数了
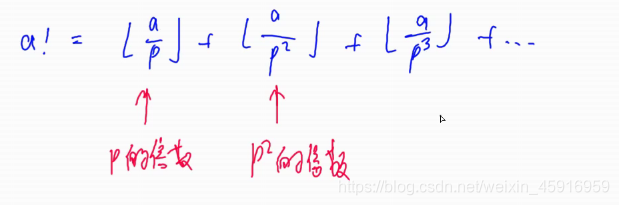
以上为求:n得阶乘里面包含的p的个数。
一、筛质数(线性筛法)
二、求每个质数的次数
三。用高精度乘法将所有的质因子乘到一块去
答案
#include<bits/stdc++.h>
using namespace std;
const int N = 5010;
int primes[N], cnt;
int sum[N];
bool st[N];
void get_primes(int n){
for(int i = 2; i <= n; i ++){
if(!st[i])
primes[cnt ++ ] = i;
for(int j = 0 ;primes[j] <= n / i; j ++){
st[primes[j] * i] = 1;
if(i % primes[j] == 0)
break;
}
}
}
int get(int n, int p){
int res = 0;
while(n){
res += n / p;
n /= p;
}
return res;
}
vector<int> mul(vector<int> a, int b){
vector <int> c;
int t = 0;
for(int i = 0; i < a.size(); i ++){
t += a[i] * b;
c.push_back(t % 10);
t /= 10;
}
while(t){
c.push_back(t % 10);
t /= 10;
}
return c;
}
int main(){
int a, b;
cin >> a >> b;
get_primes(a);
for(int i = 0; i < cnt; i ++){
int p = primes[i];
sum[i] = get(a, p) - get(a - b, p) - get(b, p);
}
vector<int> res;
res.push_back(1);
for(int i = 0; i < cnt; i ++)
for(int j = 0; j < sum[i]; j ++)
res = mul(res, primes[i]);
for(int i = res.size() - 1; i >= 0; i --)
printf("%d", res[i]);
return 0;
}
5、满足条件的01序列
题目
给定n个0和n个1,它们将按照某种顺序排成长度为2n的序列,
求它们能排列成的所有序列中,能够满足任意前缀序列中0的个数都不少于1的个数的序列有多少个。
输出的答案对109+7取模。
输出格式
共一行,包含整数n。
输出格式
共一行,包含一个整数,表示答案。
数据范围
1≤n≤105
输入样例:
3
输出样例:
5
思路:卡特兰数
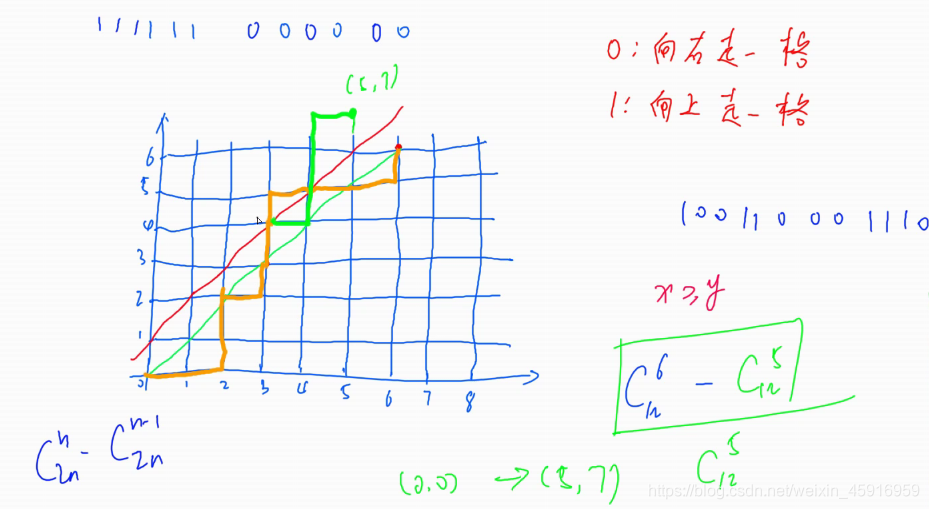

解答
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1e5 + 10, mod = 1e9 + 7;
int qmi(int a, int k, int p){
int res = 1;
while(k){
if(k & 1) res = (ll) res * a % p;
a = (ll)a *a % p;
k >>= 1;
}
return res;
}
int main(){
int n;
cin >> n;
int a = n * 2, b = n;
int res = 1;
for(int i = a; i > a - b; i --)
res = (ll) res * i % mod;
for(int i = 1; i <= b; i ++)
res = (ll) res * qmi(i, mod - 2, mod) % mod;
res = (ll)res * qmi(n + 1, mod - 2, mod) % mod;
cout << res << endl;
return 0;
}