查找算法：折半查找

折半查找，也称二分查找，是一种效率较高的查找方法。

要求线性表必须采用 顺序结构，表中元素按关键字 有序排列。

int Search_Bin (SSTable ST, KeyType key) {
  int low = 1, high = ST.length;
  while (low <= high) {  // 注意不是low<high，因为low=high时，查找区间还有最后一个结点，还要进一步比较
    int mid = (low + high) / 2;
    if (ST[mid].key == key) return mid;
    else if (ST[mid].key > key) high = mid - 1;
    else (ST[mid].key < key) low = mid + 1;
  }
  return 0;
}

注：该算法可改为递归实现

算法分析：
折半查找过程可用二叉树来描述，结点值不是记录的关键字，二是记录在表中的位置序号。
把当前查找区间的中间位置作为根，左子表和右子表分别作为根的左子树和右子树，由此得到的二叉树称为折半查找的 判定树 。

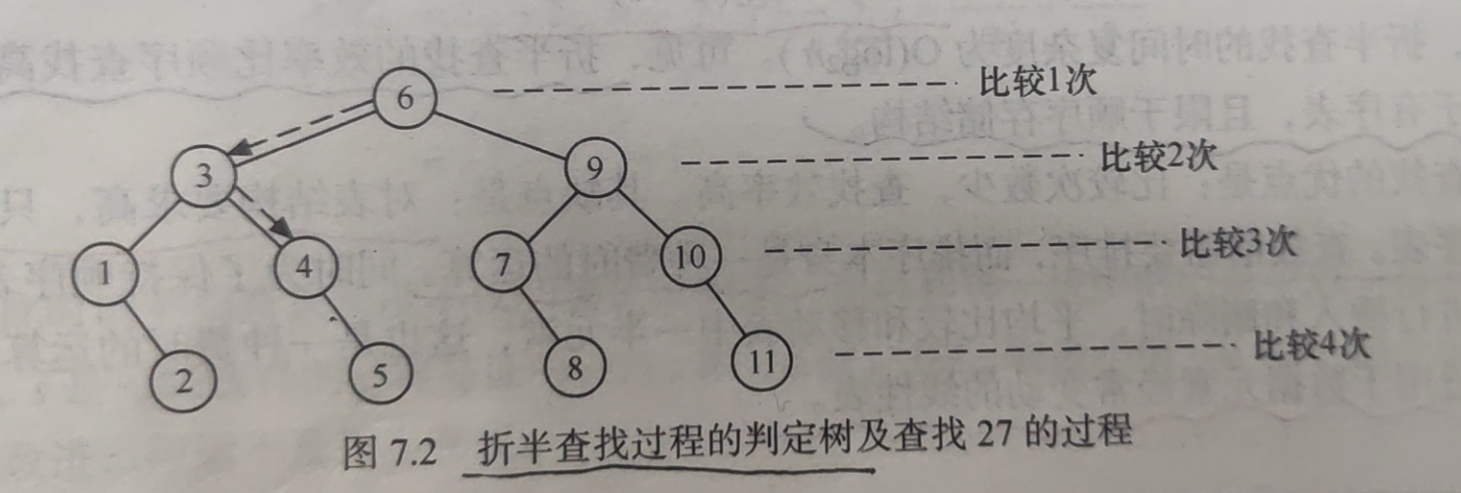
借助判定树，易得折半查找的平均查找长度。

假设有序表的长度(n=2^h - 1)，则判定表的深度(h=log_2(n+1))的满二叉树。
树中层次为(1)的结点有(1)个，层次为(2)的结点有(2)个，...，层次为(h)的结点有(2^{h-1})个。
平均查找长度

[ASL=sum_{i=1}^{n}{P_iC_i} = frac{i}{n}sum_{j=1}^{h}{j·2^{j-1}} = frac{n+1}{n}log_2(n+1)-1 ]

当n较大时，可有下列近似结果(ASL=log_2(n+1)-1)

优点：比较次数少，查找效率高
缺点：对表结构要求高，只能用于顺序存储的有序表。查找前需要排序，排序本身也会消耗时间。为保持有序性，插入和删除时，也需耗时运算。
因此， 折半查找不适用于数据元素经常变动的线性表。