一、集合
概念:
集合是指具有某种特定性质的具体的或抽象的对象汇总而成的集体。其中,构成集合的这些对象则称为该集合的元素。
基数:
集合中元素的数目称为集合基数,集合A的基数记作card(A)。当其为有限大时,集合A称为有限集,反之则为无限集
一般的,把含有有限个元素的集合叫做有限集,含无限个元素的集合叫做无限集
表示
假设有实数x < y:
①[x,y] :方括号表示包括边界,即表示x到y之间的数以及x和y;
②(x,y):小括号是不包括边界,即表示大于x、小于y的数
特性
确定性
给定一个集合,任给一个元素,该元素或者属于或者不属于该集合,二者必居其一,不允许有模棱两可的情况出现
互异性
一个集合中,任何两个元素都认为是不相同的,即每个元素只能出现一次。有时需要对同一元素出现多次的情形进行刻画,可以使用多重集,其中的元素允许出现多次
无序性
一个集合中,每个元素的地位都是相同的,元素之间是无序的。集合上可以定义序关系,定义了序关系后,元素之间就可以按照序关系排序。但就集合本身的特性而言,元素之间没有必然的序
空集
有一类特殊的集合,它不包含任何元素,如{x|x∈R x²+1=0} ,称之为空集,记为∅。空集是个特殊的集合,它有2个特点:
-
空集∅是任意一个非空集合的真子集。
-
空集是任何一个集合的子集
子集
设S,T是两个集合,如果S的所有元素都属于T ,即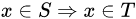
 ,则称S是T的一个真子集。
,则称S是T的一个真子集。
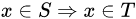
则称S是T两个子集,记为
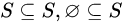
其中符号

 ,则称S是T的一个真子集。
,则称S是T的一个真子集。交并集
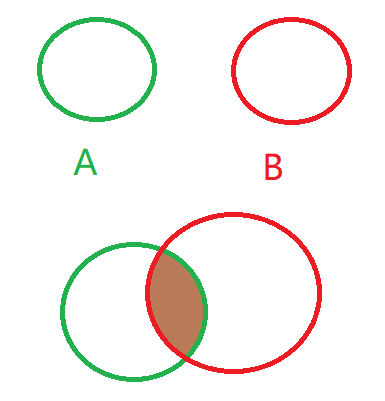
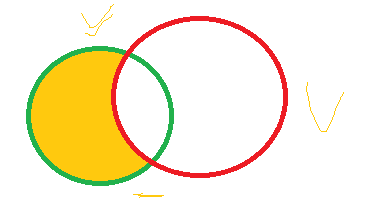
交集定义:由属于A且属于B的相同元素组成的集合记作A∩B(或B∩A),读作“A交B”(或“B交A”),即A∩B={x|x∈A,且x∈B}, 如右图所示。注意交集越交越少。若A包含B,则A∩B=B,A∪B=A
并集定义:由所有属于集合A或属于集合B的元素所组成的集合,记作A∪B(或B∪A),读作“A并B”(或“B并A”),即A∪B={x|x∈A,或x∈B},如右图所示。注意并集越并越多,这与交集的情况正相反
补集
补集又可分为相对补集和绝对补集。
相对补集定义:由属于A而不属于B的元素组成的集合,称为B关于A的相对补集,记作A-B或AB,即A-B={x|x∈A,且x∉B'}
绝对补集定义:A关于全集合U的相对补集称作A的绝对补集,记作A'或∁u(A)或~A。有U'=Φ;Φ'=U
幂集
设有集合A,由集合A所有子集组成的集合,称为集合A的幂集。对于幂集有定理如下:有限集A的幂集的基数等于2的有限集A的基数次幂
区间
实数集的子集是区间
设a,b(a<b)是两个相异的实数,则满足不等式a<x<b的所有实数x的集合称为以a,b为端点的开区间,记为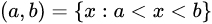
满足不等式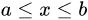 的所有实数的集合称为以a,b为端点的闭区间,记为
的所有实数的集合称为以a,b为端点的闭区间,记为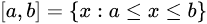
满足不等式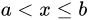 或
或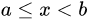 的所有实数x的集合称为以a,b为端点的半开半闭区间,分别记为
的所有实数x的集合称为以a,b为端点的半开半闭区间,分别记为
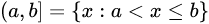 及
及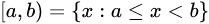
无限区间
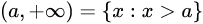
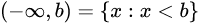
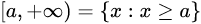
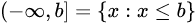
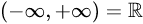
运算
交换律:A∩B=B∩A;A∪B=B∪A
结合律:A∪(B∪C)=(A∪B)∪C;A∩(B∩C)=(A∩B)∩C
分配对偶律:A∩(B∪C)=(A∩B)∪(A∩C);A∪(B∩C)=(A∪B)∩(A∪C)
对偶律:(A∪B)^C=A^C∩B^C;(A∩B)^C=A^C∪B^C
同一律:A∪∅=A;A∩U=A
求补律:A∪A'=U;A∩A'=∅
对合律:A''=A
等幂律:A∪A=A;A∩A=A
零一律:A∪U=U;A∩∅=∅
吸收律:A∪(A∩B)=A;A∩(A∪B)=A
反演律:(A∪B)'=A'∩B';(A∩B)'=A'∪B'。文字表述:1.集合A与集合B的并集的补集等于集合A的补集与集合B的补集的交集; 2.集合A与集合B的交集的补集等于集合A的补集与集合B的补集的并集。
容斥原理(特殊情况):
card(A∪B)=card(A)+card(B)-card(A∩B)
card(A∪B∪C)=card(A)+card(B)+card(C)-card(A∩B)-card(B∩C)-card(C∩A)+card(A∩B∩C)
两个集合各自独立,未产生交集,为空集∅

select * from t_ke where ke_name like '%数学%' or ke_name='程序员的自我修养' select * from t_ke where ke_name like '%数学%' union all select * from t_ke where ke_name='大学数学' -->> select * from t_ke where ke_name like '%数学%' select * from t_ke where ke_name='离散数学' select * from t_ke where ke_name like '%数学%' or ke_name='离散数学' select * from t_ke where ke_name like '%数学%' union all select * from t_ke where ke_name='离散数学' union all select 88 id,'城市建设' ke_name from dual select * from t_ke where ke_name like '%数学%' union select * from t_ke where ke_name='离散数学' union select 88 id,'城市建设' ke_name from dual
二、交集
create table t_stu2( id number primary key, user_name varchar2(10), sex varchar2(10) ); insert into t_stu2 values(1,'小军','男'); insert into t_stu2 values(2,'小黄','女'); insert into t_stu2 values(3,'小陈','男'); insert into t_stu2 values(4,'小姚','女'); commit create table t_yigong( id number primary key, user_name varchar2(10) ); insert into t_yigong values(1,'小陈'); insert into t_yigong values(2,'小姚'); insert into t_yigong values(3,'小K'); insert into t_yigong values(4,'小T'); commit select * from t_stu2 select * from t_yigong -- 想看看学生中,有那些是义工 -- 思维1:条件查询 select * from t_stu2 where user_name in (select user_name from t_yigong) -- 想看看义工中,有那些是学生 -- 思维1:条件查询 select * from t_yigong where user_name in (select user_name from t_stu2) -- 问题未必看交集的名字,只是我们要用到交集这个概念。 -- 有可能,我查询的内容根本与学生或这义工的名字毫无联系 -- 学生这个群体,愿意当义工的,女孩子多还是男孩子多? select sex,count(1) from t_stu2 where user_name in( select user_name from t_stu2 intersect select user_name from t_yigong ) group by sex insert into t_stu2 values(5,'小冰','女'); insert into t_yigong values(5,'小冰'); Commit
三、举一反三
-- 学生这个群体,不愿意当义工的,女孩子多还是男孩子多? --错误示范(99%大学生会犯的错误) select sex,count(1) from t_stu2 where user_name not in( select user_name from t_stu2 intersect select user_name from t_yigong ) group by sex -- not in就是一种排除法 -- 学习英语A,B,C,D (要排除3个才能得到正确答案) -- 对in操作:打开书本,在目录里面查询 -- 对not in操作:打开书本,800页也需要一页一页看 select * from t_stu2 select sex,count(1) from t_stu2 where user_name in( select user_name from t_stu2 minus select user_name from t_yigong ) group by sex