一.二分图的基本概念
二分图又称作二部图,是图论中的一种特殊模型。 设G=(V,E)是一个无向图,如果顶点V可分割为两个互不相交的子集(A,B),并且图中的每条边(i,j)所关联的两个顶点i和j分别属于这两个不同的顶点集(i in A,j in B),则称图G为一个二分图。
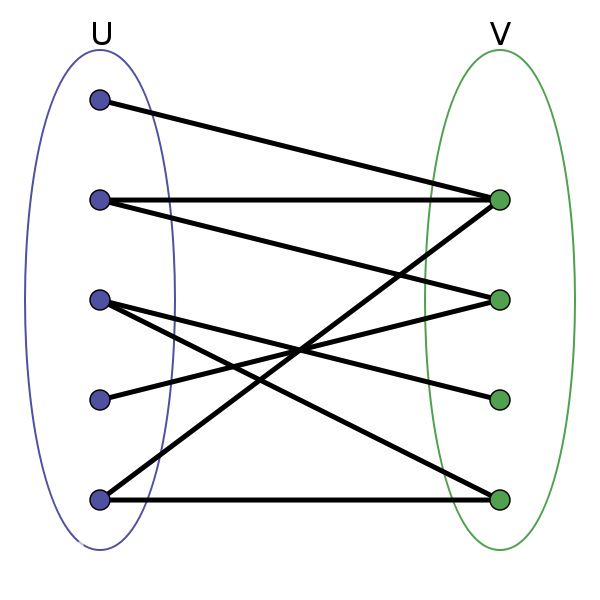
(以上内容摘自百度百科)
上面的图片就是一个二分图,左边的点之间没有直接的边相连,右边的点之间也没有直接的边相连可以分割成2个集合。
关于二分图本弱会的很少,只会最大匹配。所谓最大匹配就是左边的点和右边的点一一配对,使得最多的点有匹配时的点数。而完美匹配就是所有的点都有匹配上时的匹配。
二分图里有一个叫做增广路的东西,增广路是从左边一个未匹配边开始,沿着未匹配边,匹配边,未匹配边......走下去,并且最后停留在一个未匹配点上(未匹配点就是还没有和另一侧的点匹配的点,未匹配边就是这条边连接的2个点不匹配),这样这条路上未匹配点比匹配点多1,只要把未匹配点和匹配点互换,匹配数就又多1,所以只要有增广路存在,匹配数就可以增加。所以找最大匹配的过程就是找增广路的过程。
二.求解二分图最大匹配的基本算法
二分图最大匹配的常用算法就是匈牙利算法了吧其实是窝只会这一种算法,算法的思想很简单,代码也很好写。基本思想就是:从左边的每一个点出发,遍历每一个和他相连的点,如果有一个点还没有和左边的其他点匹配,或者和他匹配的这个点可以找到其他的匹配点,那么就让这个点和开始的右边那个点匹配,ans++。高大尚的一种说法是:不断的找增广路。其实想想这个过程也确实是这样,从左边的一个未匹配点出发,沿着一条未匹配边,如果到达的点A是未匹配点,那么这就是一条增广路了(始于未匹配点,终于未匹配点),直接返回1,ans++,如果A点是一条匹配点,那么去找和A匹配的那个点,看他能不能换一个点匹配,这也就是沿着匹配边走了一步,如果A的匹配点可以换一个点,那么就把A给最开始的那个点,否则就返回0让那个点再去找别的点。算法实现过程就是这个样子的,看一下代码吧。

1 #include<iostream> 2 #include<cstring> 3 #include<cstdio> 4 using namespace std; 5 int n,m,e; 6 struct zhw{ 7 int to,last; 8 }tu[1000005]; 9 int x,y; 10 int head[1005],tot; 11 void add(int x,int y) 12 { 13 tot++,tu[tot].last=head[x],head[x]=tot,tu[tot].to=y; 14 } 15 int to[1005]; 16 bool vis[1005]; 17 //Orz yy,yy大佬说,链式前向星只是一个工具,它并不能决定图长什么样子,所以左边编号1->n,右边编号可以是1->m,即使是1到1连边,意义也是从左边的1到右边的1 18 bool find(int x) 19 { 20 for(int i=head[x];i;i=tu[i].last) 21 { 22 if(vis[tu[i].to])continue; 23 vis[tu[i].to]=1; 24 if(!to[tu[i].to]||find(to[tu[i].to])) 25 { 26 to[tu[i].to]=x;return 1; 27 } 28 } 29 return 0; 30 } 31 int ans; 32 int main() 33 { 34 scanf("%d%d%d",&n,&m,&e); 35 for(int i=1;i<=e;++i) 36 { 37 scanf("%d%d",&x,&y); 38 if(y>m||x>n)continue; 39 add(x,y); 40 } 41 for(int i=1;i<=n;++i) 42 { 43 memset(vis,0,sizeof(vis)); 44 if(find(i))ans++; 45 } 46 printf("%d",ans); 47 return 0; 48 }
三.二分图染色问题
二分图染色是判断一个图是不是二分图的一个方法。原理就是二分图中每一个点与之相连的点都不能和它在同一个集合。找每一个没有被染色的点,然后染上色后,dfs找与它相连的所有点染上别的颜色,如果颜色冲突了就代表这张图不是二分图,否则就是二分图。

1 void dfs(int x,int c) 2 { 3 for(int i=head[x];i;i=tu[i].to) 4 { 5 if(!col[tu[i].to])dfs(tu[i].to,3-c);//颜色只有1和2,所以3-c就是相反的颜色 6 else if(col[tu[i].to]==c) 7 {//如果已经被染色了,而且与当前颜色相同,那就冲突了,就不是一个二分图了 8 printf("-1");exit(0); 9 } 10 } 11 } 12 for(int i=1;i<=n;++i) 13 if(!col[i])dfs(i,1);
四.一些简单的例题
1.座位安排https://www.luogu.org/problemnew/show/P2071
已知车上有N排座位,有N*2个人参加省赛,每排座位只能坐两人,且每个人都有自己想坐的排数,问最多使多少人坐到自己想坐的位置。
这题需要用到的思想是拆点,把n排座位拆成2*n个座位,2*n个人和2*n个座位分别组成二分图左边和右边的点,如果一个人想要去一个座位,那就和这一排的2个座位都连边,然后跑最大匹配就行了。

1 #include<iostream> 2 #include<cstdio> 3 #include<vector> 4 #include<cstring> 5 using namespace std; 6 //每排能坐2个人,所以可以把一排拆成2排 7 vector<int>tu[5005]; 8 int n; 9 bool vis[5005]; 10 int to[5005]; 11 int tmp1,tmp2; 12 int ans; 13 bool find(int x) 14 { 15 for(int i=0;i<tu[x].size();++i) 16 { 17 if(!vis[tu[x][i]]) 18 { 19 vis[tu[x][i]]=1; 20 if(!to[tu[x][i]]||find(to[tu[x][i]])) 21 { 22 to[tu[x][i]]=x; 23 return 1; 24 } 25 } 26 } 27 return 0; 28 } 29 int main() 30 { 31 cin>>n; 32 for(int i=1;i<=2*n;++i) 33 { 34 scanf("%d%d",&tmp1,&tmp2); 35 tu[i].push_back(tmp2+n),tu[i].push_back(tmp2); 36 tu[i].push_back(tmp1),tu[i].push_back(tmp1+n); 37 } 38 for(int i=1;i<=2*n;++i) 39 { 40 memset(vis,0,sizeof(vis)); 41 if(find(i))ans++; 42 } 43 printf("%d",ans); 44 }
2.完美的牛栏https://www.luogu.org/problemnew/show/P1894
农夫约翰上个星期刚刚建好了他的新牛棚,他使用了最新的挤奶技术。不幸的是,由于工程问题,每个牛栏都不一样。第一个星期,农夫约翰随便地让奶牛们进入牛栏,但是问题很快地显露出来:每头奶牛都只愿意在她们喜欢的那些牛栏中产奶。上个星期,农夫约翰刚刚收集到了奶牛们的爱好的信息(每头奶牛喜欢在哪些牛栏产奶)。一个牛栏只能容纳一头奶牛,当然,一头奶牛只能在一个牛栏中产奶。
给出奶牛们的爱好的信息,计算最大分配方案。
裸的二分图匹配。

1 //二分图最大匹配 2 #include<iostream> 3 #include<cstdio> 4 #include<cstring> 5 using namespace std; 6 int n,m; 7 int f[210][210]; 8 int ans; 9 int tmp,tmp2; 10 int to[210]; 11 bool vis[210]; 12 bool find(int x) 13 { 14 for(int i=1;i<=m;++i) 15 if(f[x][i]&&(!vis[i])) 16 { 17 vis[i]=1; 18 if(!to[i]||find(to[i])) 19 { 20 to[i]=x; 21 return 1; 22 } 23 } 24 return 0; 25 } 26 int main() 27 { 28 scanf("%d%d",&n,&m); 29 for(int i=1;i<=n;++i) 30 { 31 scanf("%d",&tmp); 32 for(int j=1;j<=tmp;++j) 33 { 34 scanf("%d",&tmp2); 35 f[i][tmp2]=1; 36 } 37 } 38 for(int i=1;i<=n;++i) 39 { 40 memset(vis,0,sizeof(vis)); 41 if(find(i))ans++; 42 } 43 printf("%d ",ans); 44 return 0; 45 }
3.飞行员配对方案问题https://www.luogu.org/problemnew/show/P2756
英国皇家空军从沦陷国征募了大量外籍飞行员。由皇家空军派出的每一架飞机都需要配备在航行技能和语言上能互相配合的2 名飞行员,其中1 名是英国飞行员,另1名是外籍飞行员。在众多的飞行员中,每一名外籍飞行员都可以与其他若干名英国飞行员很好地配合。如何选择配对飞行的飞行员才能使一次派出最多的飞机。对于给定的外籍飞行员与英国飞行员的配合情况,试设计一个算法找出最佳飞行员配对方案,使皇家空军一次能派出最多的飞机。
对于给定的外籍飞行员与英国飞行员的配合情况,编程找出一个最佳飞行员配对方案,使皇家空军一次能派出最多的飞机。
英籍和外籍飞行员最大匹配。

1 //二分图 2 #include<iostream> 3 #include<cstdio> 4 #include<cstring> 5 #include<algorithm> 6 using namespace std; 7 int n,m; 8 int f[110][110]; 9 int x,y; 10 bool vis[110]; 11 int to[110]; 12 struct node{ 13 int to,last; 14 }tu[1000000]; 15 int head[110],tot; 16 void add(int from,int to) 17 { 18 tot++; 19 tu[tot].last=head[from],head[from]=tot; 20 tu[tot].to=to; 21 } 22 bool find(int x) 23 { 24 for(int i=head[x];i!=-1;i=tu[i].last) 25 { 26 int t=tu[i].to; 27 if(!vis[t]) 28 { 29 vis[t]=1; 30 if(!to[t]||find(to[t])) 31 { 32 to[t]=x; 33 return 1; 34 } 35 } 36 } 37 return 0; 38 } 39 int ans; 40 int main() 41 { 42 memset(head,-1,sizeof(head)); 43 scanf("%d%d",&m,&n); 44 for(;;) 45 { 46 scanf("%d%d",&x,&y); 47 if(x==-1)break; 48 add(x,y); 49 } 50 for(int i=1;i<=m;++i) 51 { 52 memset(vis,0,sizeof(vis)); 53 if(find(i))ans++; 54 } 55 cout<<ans<<endl; 56 for(int i=m+1;i<=n;++i) 57 if(to[i])cout<<to[i]<<" "<<i<<endl; 58 return 0; 59 }
