AVL树（自平衡树）——c++实现

 

 

AVL树是高度平衡的而二叉树。它的特点是：AVL树中任何节点的两个子树的高度最大差别为1。 

AVL树本质上还是一棵二叉搜索树，它的特点是：

1.本身首先是一棵二叉搜索树。

2.带有平衡条件：每个结点的左右子树的高度之差的绝对值（平衡因子）最多为1。

也就是说，AVL树，本质上是带了平衡功能的二叉查找树（二叉排序树，二叉搜索树）。

既然是树，那么就要有节点：

template <class T>
struct AVLTreeNode{
    T data;
    int height;
    AVLTreeNode* Left;
    AVLTreeNode* Right;
    
    AVLTreeNode(T v,AVLTreeNode* l,AVLTreeNode* r):data(v),height(0),Left(l),Right(r){}
};
/*
数据解释：
data用来储存节点值
height储存的是几点的高度
Left是左儿子
Right是右儿子
最后一项是构造函数
*/

接下来我们给出AVL树的定义

template <class T> 
class AVLTree{
    private:
                //根节点
        AVLTreeNode<T>* Root;
    public:
        AVLTree():Root(NULL){}//构造函数
        
        void add(T data);//添加节点的外部接口
        int height();//查询高度的外部接口
        int max(int a, int b);//比较两个数据的大小
    private:
        AVLTreeNode<T>* add(AVLTreeNode<T>* &tree, T data);//添加节点的内部接口
        int height(AVLTreeNode<T>* tree);//查询高度的内部接口
        AVLTreeNode<T>* LL_Rotation(AVLTreeNode<T>* k2);//左左旋转的具体实现
        AVLTreeNode<T>* RR_Rotation(AVLTreeNode<T>* k1);//右右旋转的具体实现
        AVLTreeNode<T>* LR_Rotation(AVLTreeNode<T>* k3);//左右旋转的具体实现
        AVLTreeNode<T>* RL_Rotation(AVLTreeNode<T>* k1);//右左旋转的具体实现
        
};   

1.查询高度

/*
高度
作用：获取树的高度 
*/
template <class T>
int AVLTree<T>::height(AVLTreeNode<T>* tree) 
{
    if (tree != NULL)
        return tree->height;

    return 0;
}

template <class T>
int AVLTree<T>::height() {
    return height(Root);
}

2.比较大小

/* 模板类改造比较两个值的大小*/
template <class T>
int AVLTree<T>::max(int a, int b) {
    return a>b ? a : b;
}

3.旋转

如果在AVL树中进行插入或删除节点后，可能导致AVL树失去平衡。这种失去平衡的可以概括为4种姿态：LL(左左)，LR(左右)，RR(右右)和RL(右左)。下面给出它们的示意图：

上图中的4棵树都是"失去平衡的AVL树"，从左往右的情况依次是：LL、LR、RL、RR。除了上面的情况之外，还有其它的失去平衡的AVL树，如下图：

上面的两张图都是为了便于理解，而列举的关于"失去平衡的AVL树"的例子。总的来说，AVL树失去平衡时的情况一定是LL、LR、RL、RR这4种之一，它们都由各自的定义：

(1) LL：LeftLeft，也称为"左左"。插入或删除一个节点后，根节点的左子树的左子树还有非空子节点，导致"根的左子树的高度"比"根的右子树的高度"大2，导致AVL树失去了平衡。
     例如，在上面LL情况中，由于"根节点(8)的左子树(4)的左子树(2)还有非空子节点"，而"根节点(8)的右子树(12)没有子节点"；导致"根节点(8)的左子树(4)高度"比"根节点(8)的右子树(12)"高2。

(2) LR：LeftRight，也称为"左右"。插入或删除一个节点后，根节点的左子树的右子树还有非空子节点，导致"根的左子树的高度"比"根的右子树的高度"大2，导致AVL树失去了平衡。
     例如，在上面LR情况中，由于"根节点(8)的左子树(4)的左子树(6)还有非空子节点"，而"根节点(8)的右子树(12)没有子节点"；导致"根节点(8)的左子树(4)高度"比"根节点(8)的右子树(12)"高2。

(3) RL：RightLeft，称为"右左"。插入或删除一个节点后，根节点的右子树的左子树还有非空子节点，导致"根的右子树的高度"比"根的左子树的高度"大2，导致AVL树失去了平衡。
     例如，在上面RL情况中，由于"根节点(8)的右子树(12)的左子树(10)还有非空子节点"，而"根节点(8)的左子树(4)没有子节点"；导致"根节点(8)的右子树(12)高度"比"根节点(8)的左子树(4)"高2。

(4) RR：RightRight，称为"右右"。插入或删除一个节点后，根节点的右子树的右子树还有非空子节点，导致"根的右子树的高度"比"根的左子树的高度"大2，导致AVL树失去了平衡。
     例如，在上面RR情况中，由于"根节点(8)的右子树(12)的右子树(14)还有非空子节点"，而"根节点(8)的左子树(4)没有子节点"；导致"根节点(8)的右子树(12)高度"比"根节点(8)的左子树(4)"高2。

前面说过，如果在AVL树中进行插入或删除节点后，可能导致AVL树失去平衡。AVL失去平衡之后，可以通过旋转使其恢复平衡，下面分别介绍"LL(左左)，LR(左右)，RR(右右)和RL(右左)"这4种情况对应的旋转方法。

3.1LL旋转

/*
LL
在左左旋转中，一共涉及到三代节点，我们把爷爷节点命名为K2，K2的左儿子命名为K1。
问题出现的原因是K1的左儿子增加了一个节点导致平衡树失衡
解决思路：
    让K1成为爷爷节点，K2成为K1的右儿子，并且将K1的右儿子接为K2的左儿子，然后返回爷爷节点K1取代原来K2的位置 
*/ 
template <class T>
AVLTreeNode<T>* AVLTree<T>::LL_Rotation(AVLTreeNode<T>* k2){
    AVLTreeNode<T>* k1;

    k1 = k2->Left;
    k2->Left = k1->Right;
    k1->Right = k2;

    k2->height = max( height(k2->Left), height(k2->Right)) + 1;
    k1->height = max( height(k1->Left), k2->height) + 1;

    return k1;
}

3.2RR旋转

/*
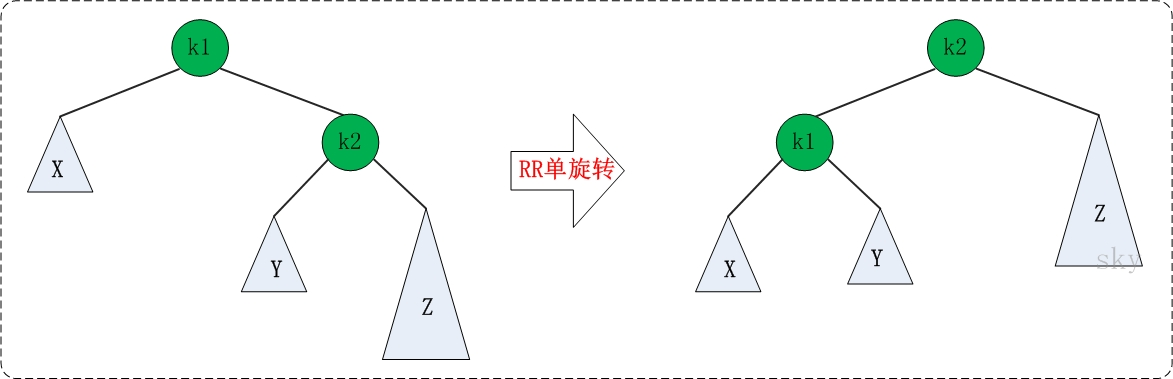
RR
在右右旋转中，一共涉及到三代节点，我们把爷爷节点命名为K1，K1的右儿子命名为K2。
问题出现的原因是K2的右儿子增加了一个节点导致平衡树失衡
解决思路：
    让K2成为爷爷节点，K1成为K2的左儿子，并且将K2的左儿子接为K1的右儿子，然后返回爷爷节点K2取代原来K1的位置 
*/ 
template <class T>
AVLTreeNode<T>* AVLTree<T>::RR_Rotation(AVLTreeNode<T>* k1){
    AVLTreeNode<T>* k2;

    k2 = k1->Right;
    k1->Right = k2->Left;
    k2->Left = k1;

    k1->height = max( height(k1->Left), height(k1->Right)) + 1;
    k2->height = max( height(k2->Right), k1->height) + 1;

    return k2;
}

3.3LR旋转

/*
LR
在左右旋转中，一共涉及到四代节点，我们把做根本的节点成为K3（曾爷爷节点），K3的左儿子称为K1（爷爷节点），K1的右儿子称为K2
问题出现的原因时K2的右儿子增加了一个节点之后导致树的失衡
解决思路：
    因为涉及到四代节点，所以需要两次旋转，
    首先对K1，K2进行一次右右旋转 =》 K2成为爷爷节点（即K3的左儿子），k2原本的左儿子称为K1的右儿子，K1成为K2的左儿子 
    接下来对K2，K3进行一次左左旋转 =》K2称为曾爷爷节点，K2原本的右儿子成为K3的左儿子，K3成为K2的右儿子  
*/
template <class T>
AVLTreeNode<T>* AVLTree<T>::LR_Rotation(AVLTreeNode<T>* k3){
    k3->Left = RR_Rotation(k3->Left);

    return LL_Rotation(k3);
}

3.4RL旋转

/*
RL
在右左旋转中，一共涉及到四代节点，我们把做根本的节点成为K1（曾爷爷节点），K1的右儿子称为K3（爷爷节点），K3的左儿子称为K2
问题出现的原因时K2的左儿子增加了一个节点之后导致树的失衡
解决思路：
    因为涉及到四代节点，所以需要两次旋转，
    首先对K2，K3进行一次左左旋转 =》 K2成为爷爷节点（即K1的右儿子），k2原本的右儿子称为K3的左儿子，K3成为K2的右儿子 
    接下来对K1，K2进行一次右右旋转 =》K2称为曾爷爷节点，K2原本的左儿子成为K1的右儿子，K1成为K2的左儿子  
*/
template <class T>
AVLTreeNode<T>* AVLTree<T>::RL_Rotation(AVLTreeNode<T>* k1){
    k1->Right = LL_Rotation(k1->Right);

    return RR_Rotation(k1);
}

 4.插入节点

template <class T>
AVLTreeNode<T>* AVLTree<T>::add(AVLTreeNode<T>* &tree, T data){
    if (tree == NULL) {
        tree = new AVLTreeNode<T>(data, NULL, NULL);
    }
    else if (data < tree->data){ 
        //将新加入的节点插入左子树 
        tree->Left = add(tree->Left, data);
        //检查加入新的结点之后树是否失去平衡 
        if (height(tree->Left) - height(tree->Right) == 2)
        {
            if (data < tree->Left->data)
                tree = LL_Rotation(tree);//左左，新加入之后左儿子的左儿子深了  
            else
                tree = LR_Rotation(tree);//左右，新加入之后左儿子的右儿子深了
        }
    }
    //将新加入的节点插入右子树 
    else if (data > tree->data) {
        tree->Right = add(tree->Right, data);
        //检查加入新的结点之后树是否失去平衡 
        if (height(tree->Right) - height(tree->Left) == 2)
        {
            if (data > tree->Right->data)
                tree = RR_Rotation(tree);//右右，新加入之后右儿子的右儿子深了  
            else
                tree = RL_Rotation(tree);//右左，新加入之后右儿子的左儿子深了  
        }
    }
    else //该节点已经在树中 
    {
        cout << "该节点已经存在树中" << endl;
    }
    //更新更前当前节点的高度 
    tree->height = max( height(tree->Left), height(tree->Right)) + 1;

    return tree;
}

template <class T>
void AVLTree<T>::add(T data){
    add(Root, data);
}

总的代码：

#include <cstdio>
#include <iostream>

using namespace std;

template <class T>
struct AVLTreeNode{
    T data;
    int height;
    AVLTreeNode* Left;
    AVLTreeNode* Right;
    
    AVLTreeNode(T v,AVLTreeNode* l,AVLTreeNode* r):data(v),height(0),Left(l),Right(r){}
};
/*
AVL树的定义
为了保护类内数据，仿照网络实例把函数写成了内接口和外接口的形式。还有模板类。 
感觉代码有点繁杂，写完之后调式的时候感觉不太顺手，以后写程序要注意内接口和外接口的模式 
*/
template <class T> 
class AVLTree{
    private:
        AVLTreeNode<T>* Root;
    public:
        AVLTree():Root(NULL){}
        
        void add(T data);
        int height();
        int max(int a, int b);
    private:
        AVLTreeNode<T>* add(AVLTreeNode<T>* &tree, T data);
        int height(AVLTreeNode<T>* tree);
        AVLTreeNode<T>* LL_Rotation(AVLTreeNode<T>* k2);
        AVLTreeNode<T>* RR_Rotation(AVLTreeNode<T>* k1);
        AVLTreeNode<T>* LR_Rotation(AVLTreeNode<T>* k3);
        AVLTreeNode<T>* RL_Rotation(AVLTreeNode<T>* k1);
        
};
/*
高度
作用：获取树的高度 
*/
template <class T>
int AVLTree<T>::height(AVLTreeNode<T>* tree) 
{
    if (tree != NULL)
        return tree->height;

    return 0;
}

template <class T>
int AVLTree<T>::height() {
    return height(Root);
}
/* 模板类改造比较两个值的大小*/
template <class T>
int AVLTree<T>::max(int a, int b) {
    return a>b ? a : b;
}

/*
LL
在左左旋转中，一共涉及到三代节点，我们把爷爷节点命名为K2，K2的左儿子命名为K1。
问题出现的原因是K1的左儿子增加了一个节点导致平衡树失衡
解决思路：
    让K1成为爷爷节点，K2成为K1的右儿子，并且将K1的右儿子接为K2的左儿子，然后返回爷爷节点K1取代原来K2的位置 
*/ 
template <class T>
AVLTreeNode<T>* AVLTree<T>::LL_Rotation(AVLTreeNode<T>* k2){
    AVLTreeNode<T>* k1;

    k1 = k2->Left;
    k2->Left = k1->Right;
    k1->Right = k2;

    k2->height = max( height(k2->Left), height(k2->Right)) + 1;
    k1->height = max( height(k1->Left), k2->height) + 1;

    return k1;
}
/*
RR
在右右旋转中，一共涉及到三代节点，我们把爷爷节点命名为K1，K1的右儿子命名为K2。
问题出现的原因是K2的右儿子增加了一个节点导致平衡树失衡
解决思路：
    让K2成为爷爷节点，K1成为K2的左儿子，并且将K2的左儿子接为K1的右儿子，然后返回爷爷节点K2取代原来K1的位置 
*/ 
template <class T>
AVLTreeNode<T>* AVLTree<T>::RR_Rotation(AVLTreeNode<T>* k1){
    AVLTreeNode<T>* k2;

    k2 = k1->Right;
    k1->Right = k2->Left;
    k2->Left = k1;

    k1->height = max( height(k1->Left), height(k1->Right)) + 1;
    k2->height = max( height(k2->Right), k1->height) + 1;

    return k2;
}
/*
LR
在左右旋转中，一共涉及到四代节点，我们把做根本的节点成为K3（曾爷爷节点），K3的左儿子称为K1（爷爷节点），K1的右儿子称为K2
问题出现的原因时K2的右儿子增加了一个节点之后导致树的失衡
解决思路：
    因为涉及到四代节点，所以需要两次旋转，
    首先对K1，K2进行一次右右旋转 =》 K2成为爷爷节点（即K3的左儿子），k2原本的左儿子称为K1的右儿子，K1成为K2的左儿子 
    接下来对K2，K3进行一次左左旋转 =》K2称为曾爷爷节点，K2原本的右儿子成为K3的左儿子，K3成为K2的右儿子  
*/
template <class T>
AVLTreeNode<T>* AVLTree<T>::LR_Rotation(AVLTreeNode<T>* k3){
    k3->Left = RR_Rotation(k3->Left);

    return LL_Rotation(k3);
}
/*
RL
在右左旋转中，一共涉及到四代节点，我们把做根本的节点成为K1（曾爷爷节点），K1的右儿子称为K3（爷爷节点），K3的左儿子称为K2
问题出现的原因时K2的左儿子增加了一个节点之后导致树的失衡
解决思路：
    因为涉及到四代节点，所以需要两次旋转，
    首先对K2，K3进行一次左左旋转 =》 K2成为爷爷节点（即K1的右儿子），k2原本的右儿子称为K3的左儿子，K3成为K2的右儿子 
    接下来对K1，K2进行一次右右旋转 =》K2称为曾爷爷节点，K2原本的左儿子成为K1的右儿子，K1成为K2的左儿子  
*/
template <class T>
AVLTreeNode<T>* AVLTree<T>::RL_Rotation(AVLTreeNode<T>* k1){
    k1->Right = LL_Rotation(k1->Right);

    return RR_Rotation(k1);
}

template <class T>
AVLTreeNode<T>* AVLTree<T>::add(AVLTreeNode<T>* &tree, T data){
    if (tree == NULL) {
        tree = new AVLTreeNode<T>(data, NULL, NULL);
    }
    else if (data < tree->data){ 
        //将新加入的节点插入左子树 
        tree->Left = add(tree->Left, data);
        //检查加入新的结点之后树是否失去平衡 
        if (height(tree->Left) - height(tree->Right) == 2)
        {
            if (data < tree->Left->data)
                tree = LL_Rotation(tree);//左左，新加入之后左儿子的左儿子深了  
            else
                tree = LR_Rotation(tree);//左右，新加入之后左儿子的右儿子深了
        }
    }
    //将新加入的节点插入右子树 
    else if (data > tree->data) {
        tree->Right = add(tree->Right, data);
        //检查加入新的结点之后树是否失去平衡 
        if (height(tree->Right) - height(tree->Left) == 2)
        {
            if (data > tree->Right->data)
                tree = RR_Rotation(tree);//右右，新加入之后右儿子的右儿子深了  
            else
                tree = RL_Rotation(tree);//右左，新加入之后右儿子的左儿子深了  
        }
    }
    else //该节点已经在树中 
    {
        cout << "该节点已经存在树中" << endl;
    }
    //更新更前当前节点的高度 
    tree->height = max( height(tree->Left), height(tree->Right)) + 1;

    return tree;
}

template <class T>
void AVLTree<T>::add(T data){
    add(Root, data);
}

int main(){
    int num;
    AVLTree<int>* tree=new AVLTree<int>();
    cin>>num;
    for(int i=0;i<num;i++){
        int x;
        cin>>x;
        tree->add(x);
    } 
    cout<<"高度为："<<tree->height()<<endl; 
    return 0;
}
/*
实例输入：
16
3 2 1 4 5 6 7 16 15 14 13 12 11 10 8 9
实例输出：
5 
*/

 源自：http://www.cnblogs.com/skywang12345/p/3577360.html