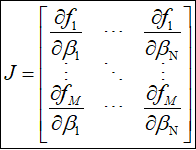基于blog: https://blog.csdn.net/qq_39521554/article/details/79919041 加上本人理解,整理下资料以便深入理解.
在学习SLAM过程中,涉及一些非线性优化问题,最后都转换成了求解非线性最小二乘的问题。
有很多求解方式:梯度下降法,牛顿法,高斯牛顿法(Gauss Newton),列文伯格-马尔夸特法 (Levenberg-Marquardt)
总结这几种方式的不同:

其中高斯牛顿法相比牛顿法是使用雅可比的转置乘以雅可比来表示黑塞矩阵,简便了计算。
其中列文伯格-马尔夸特法是在高斯牛顿法的黑塞矩阵加了正定项。
本文主要介绍,高斯牛顿法(Gauss Newton):
观测值(已知):
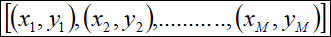
函数值(求解):

问题描述:
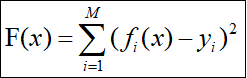
我们需要找到一组 使得 F(x)最小
使得 F(x)最小
雅可比矩阵表示为: