好的,我们先来看题:
题目描述
给定一棵有n个点的树
询问树上距离为k的点对是否存在。
输入输出格式
输入格式:
n,m 接下来n-1条边a,b,c描述a到b有一条长度为c的路径
接下来m行每行询问一个K
输出格式:
对于每个K每行输出一个答案,存在输出“AYE”,否则输出”NAY”(不包含引号)
输入输出样例
说明
对于30%的数据n<=100
对于60%的数据n<=1000,m<=50
对于100%的数据n<=10000,m<=100,c<=1000,K<=10000000
1.什么是点分治?
首先,分治大家应该很了解了吧,那么点分治其实与分治同理,就是将复杂的问题分解为很多很多细小的子问题,从而减少时间复杂度,就拿这道题来说,利用点分治就明显比爆搜快很多。。。
2.点分治的原理:
先来看一张图片(不错,是我盗的图(滑稽。。。))
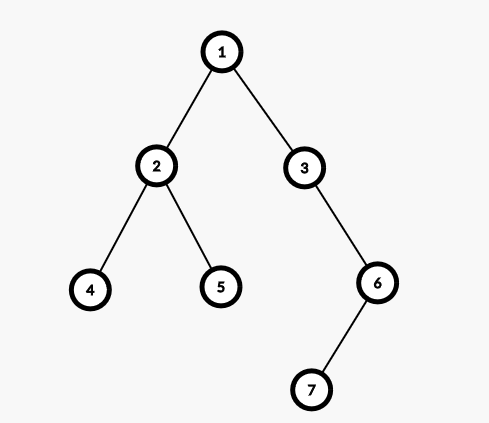
显然我们如果要求两点之间的距离,只有两种情况:经过根节点或者不经过根节点。并且第二种情况可以通过换根来转化为第一种情况,那么我们就可以愉快的进行分治了qaq
3.如何实现?
上面提到了一些原理,但是如果是这样的一张图呢?
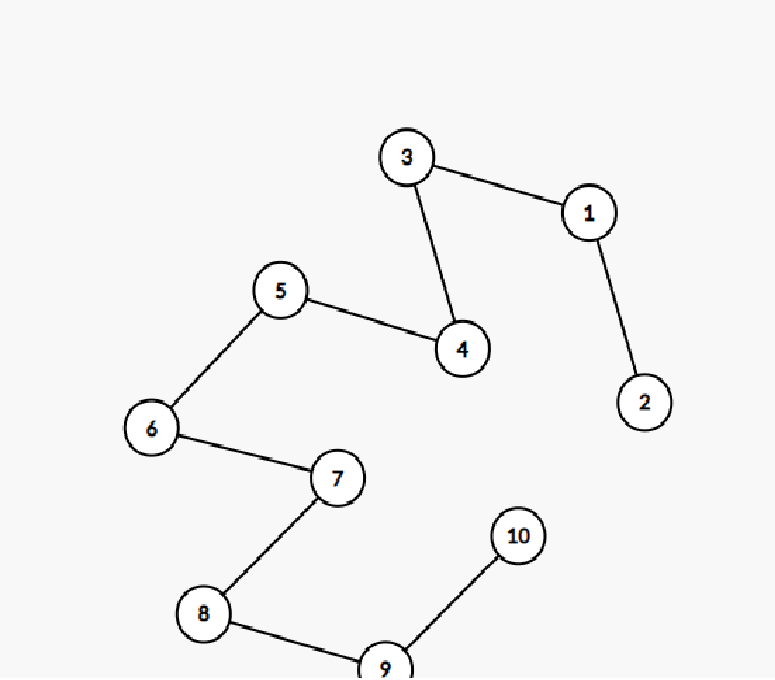
如果还是找根的的话你基本就凉凉了。。。
因此,我们期望将分成的两个树越平均越好,重心就诞生啦!!!
树重心的定义:找到一个点,其所有的子树中最大的子鼠节点数最少,那么这个点就是这棵鼠的重心,删去重心后,生成的多棵鼠尽可能平衡(不知道知否正确)
4.重点来了!!!
铺垫基本做完了,现在来讲这道题:
其实也是比较简单的,由于没有强制在线,所以可以离线操作(废话)。
我们从重心开始枚举子树的根节点,依次递归下去,每一次遇到满足题意的就++就可以啦!
最后,附上本题代码:(代码中有详解qaq)
1 #include<cstdio> 2 #include<algorithm> 3 using namespace std; 4 const int inf=10000000; 5 const int maxn=100010; 6 struct EDGE//链前存边 7 { 8 int to,val,nxt; 9 } edge[maxn<<1]; 10 int head[maxn]/*链前附带物*/,cnt/*边数*/,maxp[maxn]/*子树的最大大小*/,size[maxn]/*子树大小*/,dis[maxn]/*x点到重心的距离*/; 11 int vis[maxn]/*访问标记*/,test[105]/*记录是否可行*/,ju[inf]/*判断是否存在这个距离*/,q[maxn]/*用于清除ju数组*/,rem[maxn]/*记录距离*/; 12 int query[1010]/*记录询问*/; 13 int sum/*(子)树的大小和*/,root/*重心*/,n,m; 14 void add(int x,int y,int z)//链前加边 15 { 16 edge[++cnt].val=z; 17 edge[cnt].to=y; 18 edge[cnt].nxt=head[x]; 19 head[x]=cnt; 20 } 21 void getroot(int id,int fa)//找重心 22 { 23 size[id]=1; 24 maxp[id]=0; 25 for(int i=head[id]; i; i=edge[i].nxt)//链前遍历 26 { 27 if(edge[i].to==fa||vis[edge[i].to]!=0) 28 { 29 continue; 30 } 31 getroot(edge[i].to,id); 32 size[id]+=size[edge[i].to];//回溯时的大小加和 33 maxp[id]=max(size[edge[i].to],maxp[id]);//记录子树大小的最大值 34 } 35 maxp[id]=max(maxp[id],sum-size[id]);//判断两个子树大小,记录最大值 36 if(maxp[id]<maxp[root])//判断所选重心是否合法 37 { 38 root=id; 39 } 40 } 41 void getdis(int id,int fa)//求距离,没啥好说的吧。。。 42 { 43 rem[++rem[0]]=dis[id]; 44 for(int i=head[id]; i; i=edge[i].nxt) 45 { 46 if(edge[i].to==fa||vis[edge[i].to]!=0) 47 { 48 continue; 49 } 50 dis[edge[i].to]=dis[id]+edge[i].val; 51 getdis(edge[i].to,id); 52 } 53 } 54 void clac(int id) 55 { 56 int now=0; 57 for(int i=head[id]; i; i=edge[i].nxt) 58 { 59 if(vis[edge[i].to]!=0) 60 { 61 continue; 62 } 63 rem[0]=0;//利用rem【0】来实现一个变量的作用 64 dis[edge[i].to]=edge[i].val;//加上邻边的距离 65 getdis(edge[i].to,id);//继续向下找 66 for(int j=rem[0]; j; j--) 67 { 68 for(int k=1; k<=m; k++)//枚举每一个询问 69 { 70 if(query[k]>=rem[j])//如果大于或等于则找另一半 71 { 72 test[k]|=ju[query[k]-rem[j]];//右面一项为1就返回1,为0就返回0 73 } 74 } 75 } 76 for(int j=rem[0]; j; j--)//存入可行解 77 { 78 q[++now]=rem[j]; 79 ju[rem[j]]=1; 80 } 81 } 82 for(int i=1; i<=now; i++)//清零 83 { 84 ju[q[i]]=0; 85 } 86 } 87 void slove(int id) 88 { 89 vis[id]=ju[0]=1;//标记为找过 90 clac(id);//以id为根进行扩散 91 for(int i=head[id]; i; i=edge[i].nxt)//逐个遍历 92 { 93 if(vis[edge[i].to]!=0) 94 { 95 continue; 96 } 97 sum=size[edge[i].to];//更新sum值为目前to点的子树大小总和 98 root=0; 99 maxp[root]=inf; 100 getroot(edge[i].to,0); 101 slove(root);//逐个判断 102 } 103 } 104 int main() 105 { 106 scanf("%d%d",&n,&m); 107 for(int i=1; i<=n-1; i++)//加边 108 { 109 int x,y,z; 110 scanf("%d%d%d",&x,&y,&z); 111 add(x,y,z); 112 add(y,x,z); 113 } 114 for(int i=1; i<=m; i++)//储存询问的要求 115 { 116 scanf("%d",&query[i]); 117 } 118 maxp[root]=sum=n;//初始将其设为最大,从而确定重心 119 getroot(1,0);//找重心 120 slove(root);//开干 121 for(int i=1; i<=m; i++)//华丽的输出结果 122 { 123 if(test[i]!=0) 124 { 125 printf("AYE "); 126 } 127 else 128 { 129 printf("NAY "); 130 } 131 } 132 return 0; 133 }