七、特征提取和转换

TF-IDF

TF-IDF(Term frequency-inverse document frequency ) 是文本挖掘中一种广泛使用的特征向量化方法。TF-IDF反映了语料中单词对文档的重要程度。假设单词用t表示，文档用d表示，语料用D表示，那么文档频度DF(t, D)是包含单词t的文档数。如果我们只是使用词频度量重要性，就会很容易过分强调重负次数多但携带信息少的单词，例如：”a”, “the”以及”of”。如果某个单词在整个语料库中高频出现，意味着它没有携带专门针对某特殊文档的信息。逆文档频度(IDF)是单词携带信息量的数值度量。

 

 

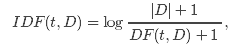
其中 |D|是语料中的文档总数。由于使用了log计算，如果单词在所有文档中出现，那么IDF就等于0。注意这里做了平滑处理（+1操作），防止单词没有在语料中出现时IDF计算中除0。TF-IDF度量是TF和IDF的简单相乘：

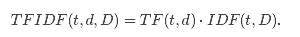
事实上词频和文档频度的定义有多重变体。在MLlib中，为了灵活性我们将TF和IDF分开处理。

MLlib中词频统计的实现使用了hashing trick（散列技巧），也就是使用哈希函数将原始特征映射到一个数字索引。然后基于这个

索引来计算词频。这个方法避免了全局的单词到索引的映射，全局映射对于大量语料有非常昂贵的计算/存储开销；但是该方法也带

来了潜在哈希冲突的问题，不同原始特征可能会被映射到相同的索引。为了减少冲突率，我们可以提升目标特征的维度，例如，哈

希表中桶的数量。默认特征维度是220 = 1048576。

 

from pyspark import SparkContext
from pyspark.mllib.feature import HashingTF

sc = SparkContext()

# Load documents (one per line).
documents = sc.textFile("...").map(lambda line: line.split(" "))

hashingTF = HashingTF()
tf = hashingTF.transform(documents)
 
from pyspark.mllib.feature import IDF

# ... continue from the previous example
tf.cache()idf = IDF().fit(tf)
tfidf = idf.transform(tf)
 
# ... continue from the previous example
tf.cache()idf = IDF(minDocFreq=2).fit(tf)
tfidf = idf.transform(tf)

Word2Vec：

Word2Vec 计算单词的向量表示。这种表示的主要优点是相似的词在向量空间中离得近，这使得向新模式的泛化更容易并且模型估计更鲁棒。向量表示在诸如命名实体识别、歧义消除、句子解析、打标签以及机器翻译等自然语言处理程序中比较有用。

Model：

MLlib中的Word2Vec实现，使用的是skip-gram模型。skip-gram的目标函数是学习擅长预测同一个句子中词的上下文的词向量表示。用数学语言表达就是，给定一个训练单词序列：w1, w2, …, wT, skip-gram模型的目标是最大化平均log似然函数(log-likelihood):

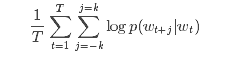
其中k是训练窗口的大小，也就是给定一个词，需要分别查看前后k个词。

 

在skip-gram模型中，每个词w跟两个向量uw和vw关联：uw是w的词向量表示，是vw上下文。给定单词wj，正确预测单词wi的概率取决于softmax模型：

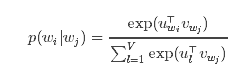
使用softmax的skip-gram模型开销很大，因为log p(wi|wj)的计算量跟V成比例，而V很可能在百万量级。为了加速Word2Vec的训练，我们引入了层次softmax，该方法将计算log p(wi|wj)时间复杂度降低到了O(log(V))。

 

from pyspark import SparkContext
from pyspark.mllib.feature import Word2Vec

sc = SparkContext(appName='Word2Vec')
inp = sc.textFile("text8_lines").map(lambda row: row.split(" "))

word2vec = Word2Vec()
model = word2vec.fit(inp)

synonyms = model.findSynonyms('china', 40)

for word, cosine_distance in synonyms:
    print("{}: {}".format(word, cosine_distance))

标准化（StandardScaler）

标准化是指：对于训练集中的样本，基于列统计信息将数据除以方差或（且）者将数据减去其均值（结果是方差等于1，数据在0附近）。这是很常用的预处理步骤。

 

例如，当所有的特征具有值为1的方差且/或值为0的均值时，SVM的径向基函数（RBF）核或者L1和L2正则化线性模型通常有更好的效果。

 

标准化可以提升模型优化阶段的收敛速度，还可以避免方差很大的特征对模型训练产生过大的影响。

 

模型拟合[Model Fitting]:

StandardScaler的构造函数具有下列参数：

withMean 默认值False. 在尺度变换（除方差）之前使用均值做居中处理（减去均值）。这会导致密集型输出，所以在稀疏数据上无效。

withStd 默认值True. 将数据缩放（尺度变换）到单位标准差。

 

StandardScaler.fit()方法以RDD[Vector]为输入，计算汇总统计信息，然后返回一个模型，该模型可以根据StandardScaler配置将输入数据转换为标准差为1，均值为0的特征。

模型中还实现了VectorTransformer，这个类可以对Vector和RDD[Vector]做转化。

 

注意：如果某特征的方差是0，那么标准化之后返回默认的0.0作为特征值。

 

from pyspark.mllib.util import MLUtils
from pyspark.mllib.linalg import Vectors
from pyspark.mllib.feature import StandardScaler

data = MLUtils.loadLibSVMFile(sc, "data/mllib/sample_libsvm_data.txt")
label = data.map(lambda x: x.label)
features = data.map(lambda x: x.features)

scaler1 = StandardScaler().fit(features)
scaler2 = StandardScaler(withMean=True, withStd=True).fit(features)
# scaler3 is an identical model to scaler2, and will produce identical transformations
scaler3 = StandardScalerModel(scaler2.std, scaler2.mean)


# data1 will be unit variance.
data1 = label.zip(scaler1.transform(features))

# Without converting the features into dense vectors, transformation with zero mean will raise
# exception on sparse vector.
# data2 will be unit variance and zero mean.
data2 = label.zip(scaler1.transform(features.map(lambda x: Vectors.dense(x.toArray())))) 

 

归一化（Normalizer）:

归一化是指将每个独立样本做尺度变换从而是该样本具有单位Lp范数。这是文本分类和聚类中的常用操作。例如，两个做了L2归一化的TF-IDF向量的点积是这两个向量的cosine（余弦）相似度。

 

Normalizer 的构造函数有以下参数：

在Lp空间的p范数, 默认p=2。

Normlizer实现了VectorTransformer ，这个类可以对Vector和RDD[Vector]做归一化。

 

注意：如果输入的范数是0，会返回原来的输入向量。

 

from pyspark.mllib.util import MLUtils
from pyspark.mllib.linalg import Vectors
from pyspark.mllib.feature import Normalizer

data = MLUtils.loadLibSVMFile(sc, "data/mllib/sample_libsvm_data.txt")
labels = data.map(lambda x: x.label)
features = data.map(lambda x: x.features)

normalizer1 = Normalizer()
normalizer2 = Normalizer(p=float("inf"))

# Each sample in data1 will be normalized using $L^2$ norm.
data1 = labels.zip(normalizer1.transform(features))

# Each sample in data2 will be normalized using $L^infty$ norm.
data2 = labels.zip(normalizer2.transform(features))

 

特征选择:

卡方选择（ChiSqSelector）:

Feature selection特征选择是指为建模过程选择最相关的特征。特征选择降低了向量空间的大小，从而降低了后续向量操作的时间复杂度。选择的特征的数量可以通过验证集来调节。

 

ChiSqSelector是指使用卡方（Chi-Squared）做特征选择。该方法操作的是有标签的类别型数据。ChiSqSelector基于卡方检验来排 序数据，然后选出卡方值较大(也就是跟标签最相关)的特征（topk)。

 

模型拟合

ChiSqSelector 的构造函数有如下特征：

 

numTopFeatures 保留的卡方较大的特征的数量。

ChiSqSelector.fit() 方法以具有类别特征的RDD[LabeledPoint]为输入，计算汇总统计信息，然后返回

ChiSqSelectorModel，这个类将输入数据转化到降维的特征空间。

 

模型实现了 VectorTransformer，这个类可以在Vector和RDD[Vector]上做卡方特征选择。

 

注意：也可以手工构造一个ChiSqSelectorModel，需要提供升序排列的特征索引。

 

import org.apache.spark.SparkConf;
import org.apache.spark.api.java.JavaRDD;
import org.apache.spark.api.java.JavaSparkContext;
import org.apache.spark.api.java.function.Function;
import org.apache.spark.mllib.feature.ChiSqSelector;
import org.apache.spark.mllib.feature.ChiSqSelectorModel;
import org.apache.spark.mllib.linalg.Vectors;
import org.apache.spark.mllib.regression.LabeledPoint;
import org.apache.spark.mllib.util.MLUtils;

SparkConf sparkConf = new SparkConf().setAppName("JavaChiSqSelector");
JavaSparkContext sc = new JavaSparkContext(sparkConf);
JavaRDD<LabeledPoint> points = MLUtils.loadLibSVMFile(sc.sc(),
    "data/mllib/sample_libsvm_data.txt").toJavaRDD().cache();

// Discretize data in 16 equal bins since ChiSqSelector requires categorical features
// Even though features are doubles, the ChiSqSelector treats each unique value as a category
JavaRDD<LabeledPoint> discretizedData = points.map(
    new Function<LabeledPoint, LabeledPoint>() {
      @Override
      public LabeledPoint call(LabeledPoint lp) {
        final double[] discretizedFeatures = new double[lp.features().size()];
        for (int i = 0; i < lp.features().size(); ++i) {
          discretizedFeatures[i] = Math.floor(lp.features().apply(i) / 16);
        }
        return new LabeledPoint(lp.label(), Vectors.dense(discretizedFeatures));
      }
    });

// Create ChiSqSelector that will select top 50 of 692 features
ChiSqSelector selector = new ChiSqSelector(50);
// Create ChiSqSelector model (selecting features)
final ChiSqSelectorModel transformer = selector.fit(discretizedData.rdd());
// Filter the top 50 features from each feature vector
JavaRDD<LabeledPoint> filteredData = discretizedData.map(
    new Function<LabeledPoint, LabeledPoint>() {
      @Override
      public LabeledPoint call(LabeledPoint lp) {
        return new LabeledPoint(lp.label(), transformer.transform(lp.features()));
      }
    });

sc.stop();

 

ElementwiseProduct：

ElementwiseProduct对输入向量的每个元素乘以一个权重向量的每个元素，对输入向量每个元素逐个进行放缩。这个称为对输入向量v 和变换向量scalingVec 使用Hadamard product(阿达玛积)进行变换，最终产生一个新的向量。用向量 w 表示 scalingVec ，则Hadamard product可以表示为

Vect(v_1, … , v_N)o Vect(w_1, … , w_N) = Vect(v_1 w_1, … , v_N w_N)

 

Hamard 乘积需要配置一个权向量 scalingVec

1) scalingVec: 变换向量

ElementwiseProduct实现 VectorTransformer 方法，就可以对向量乘以权向量，得到新的向量，或者对RDD[Vector] 乘以权向量得到RDD[Vector]

 

import java.util.Arrays;
import org.apache.spark.api.java.JavaRDD;
import org.apache.spark.api.java.JavaSparkContext;
import org.apache.spark.mllib.feature.ElementwiseProduct;
import org.apache.spark.mllib.linalg.Vector;
import org.apache.spark.mllib.linalg.Vectors;

// Create some vector data; also works for sparse vectors
JavaRDD<Vector> data = sc.parallelize(Arrays.asList(
  Vectors.dense(1.0, 2.0, 3.0), Vectors.dense(4.0, 5.0, 6.0)));
Vector transformingVector = Vectors.dense(0.0, 1.0, 2.0);
ElementwiseProduct transformer = new ElementwiseProduct(transformingVector);

// Batch transform and per-row transform give the same results:
JavaRDD<Vector> transformedData = transformer.transform(data);
JavaRDD<Vector> transformedData2 = data.map(
  new Function<Vector, Vector>() {
    @Override
    public Vector call(Vector v) {
      return transformer.transform(v);
    }
  });

 

PCA:

PCA可以将特征向量投影到低维空间，实现对特征向量的降维。

 

import org.apache.spark.mllib.regression.LinearRegressionWithSGD
import org.apache.spark.mllib.regression.LabeledPoint
import org.apache.spark.mllib.linalg.Vectors
import org.apache.spark.mllib.feature.PCA

val data = sc.textFile("data/mllib/ridge-data/lpsa.data").map { line =>
  val parts = line.split(',')
  LabeledPoint(parts(0).toDouble, Vectors.dense(parts(1).split(' ').map(_.toDouble)))
}.cache()

val splits = data.randomSplit(Array(0.6, 0.4), seed = 11L)
val training = splits(0).cache()
val test = splits(1)

val pca = new PCA(training.first().features.size/2).fit(data.map(_.features))
val training_pca = training.map(p => p.copy(features = pca.transform(p.features)))
val test_pca = test.map(p => p.copy(features = pca.transform(p.features)))

val numIterations = 100
val model = LinearRegressionWithSGD.train(training, numIterations)
val model_pca = LinearRegressionWithSGD.train(training_pca, numIterations)

val valuesAndPreds = test.map { point =>
  val score = model.predict(point.features)
  (score, point.label)}

val valuesAndPreds_pca = test_pca.map { point =>
  val score = model_pca.predict(point.features)
  (score, point.label)}

val MSE = valuesAndPreds.map{case(v, p) => math.pow((v - p), 2)}.mean()
val MSE_pca = valuesAndPreds_pca.map{case(v, p) => math.pow((v - p), 2)}.mean()

println("Mean Squared Error = " + MSE)println("PCA Mean Squared Error = " + MSE_pca)