计算机基础----数据结构

一、数据结构三要素

逻辑结构：线性结构、集合、树形结构、图形结构

存储结构：顺序存储、链式存储、索引存储、散列存储

数据的运算：定义为逻辑，实现由存储

二、算法复杂度

算法评价：时间复杂度（O(n)）+空间复杂度(S(n))

加法规则：o(n)=0(f(n))+o(g(n))=o(max(f(n),g(n)))

乘法规则：0(n)=0(f(n))*o(g(n))

 三、链表和队列

1、链表

单链表，双链表，循环链表 

2、栈和队列

栈：先进后出

队列：一头进，底端出

顺序栈

共享栈

链式栈：多个栈共享存储空间

四、数组和特殊矩阵

1、数组的存储方式

顺序存储

二维数组的两种存储方式：以行为主序，以列为主序

2、矩阵

计算：

1、以行为主序的存储结构下的二维数组a[m][n]中，任意元素a[i][j]的存储位置为：

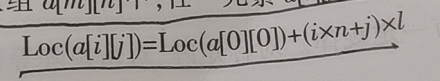
 2、对称矩阵，

行优先压缩存储上三角：

（i<=j）

 行优先压缩下三角：

(i>=j)

 3、三对角矩阵

矩阵中的任意元素在数组B中的存储位置为：2*i+j

压缩数组中下标为k的元素，在三角矩阵中的行数与列数:i=(k+1)/3，j=k-2*i

3、广义表

又称列表，是线性表的一个扩展，元素可以是一个数据元素，也可以是一个子表

广义表为非空的时候，第一个表元素为表头，其余表元素组成的表为表尾

五、树

度：节点所含有的子树棵树

叶节点：度为0的节点

树的表示方法；树形、集合文氏图、凹入表、广义表

1、二叉树

二叉树中的每个节点至多有两棵子树，左右子树次序不能随意颠倒

两种特殊二叉树：完全二叉树、满二叉树

2、二叉树

1）二叉树的计算

2）二叉树的存储结构

三种遍历方法：先序遍历，中序遍历，后序遍历

3）线索二叉树

在哪个节点的二叉树，有n+1个空链指针域，利用空链表指针存放某种遍历次序下，该节点的前趋节点和后趋节点的指针，这些指针为线索

 3、树的存储结构表示

1）双亲表示法、子女链表表示法、子女-兄弟链表表示法、广义表表示法

2）树转换为二叉树、森林，

4、树的遍历

主要分为深度遍历与广度遍历。

深度遍历分为：先序、中序、后序

广度遍历：与二叉树的层序遍历相似，分层进行访问

5、赫夫曼树

路径长度：从树的一个节点到另一个节点所经历的分支数目

树的路径长度：从树的根节点到每一个节点的路径长度之和

代权路径长度：权值*路径长度

赫夫曼编码：是数据压缩的重要方法，应用在通信领域，消除了冗余数据，提高了通信信道的传输效率

六、图

图是由顶点集合V和顶点间的关系集合E组成的一种数据结构。

无向图

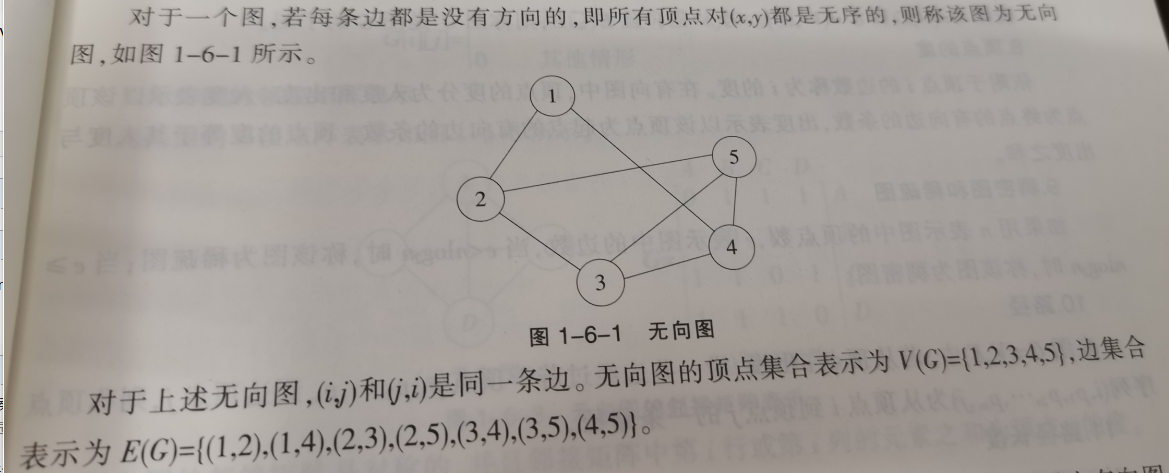
有向图

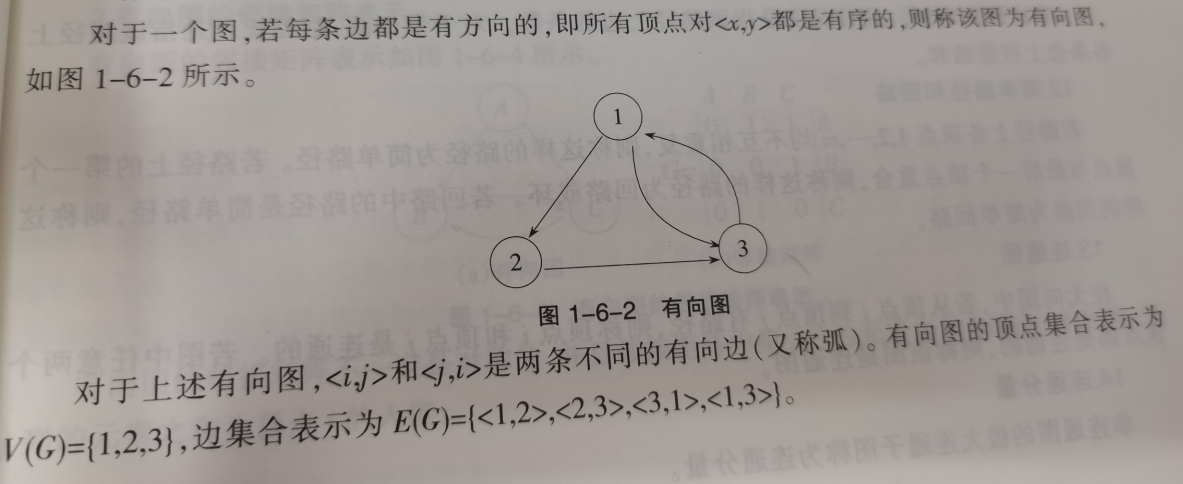
 有向完全图：每两个顶点之间都有一条边

无向完全图：每两个顶点之间都有方向相反的两条边

网络：带权图

路径长度：对于不带权的图，指该路径上边的条数；对于带权图，路径长度是指该路径上各边权值的和

连通图：在无向图中，若顶点i到顶点j有路径，则称顶点i和顶点j是联通的。若图中任意两顶点都是连通的，则称该图为连通图

连通分量：非连通图的极大连通子图

强连通图：在有向连通图中，任意两顶点之间都有相反的路径

生成树：一个无向连通图的生成树是他的极小连通子图；若是有向图，则可能得到他的由若干有向树组成的生成森林

 1、图的存储结构

邻接矩阵表示

使用两个数组来存储图：将顶点信息组织称一个定点表，利用一个邻接矩阵的二维数组来表示各顶点之间的邻接关系

无向图的邻接表示：对称，第i行会第j列的元素之和为顶点i的度

有向图的邻接表示：第i行的元素之和为顶点i的出度，第j列的元素之和为顶点j的入度

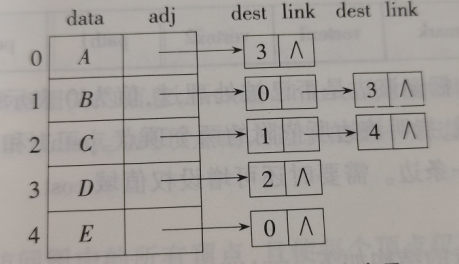
邻接表表示

邻接矩阵的额隔行分别组织成一个单链表

无向图

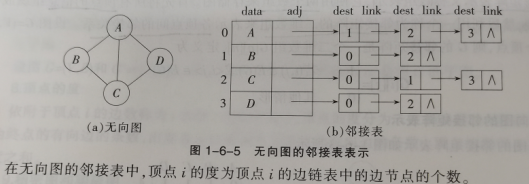
无向图中的 特点：

• 邻接表不唯一
• 若无相图中有n个顶点，e条边，则其邻接表需要、n个头结点和2e个表结点

 有向图的邻接表，以其箭头尾的数目来进行计算

 有向图的出度：顶点i对应链表中的节点数就是i的出度

有向图的入度：建立一个链接以i为头的弧的表，即逆邻接表

 多重表表示

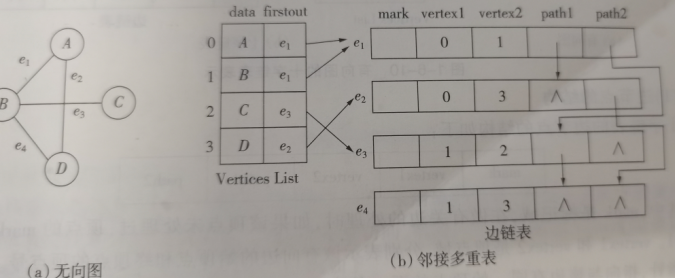
 边界点结构：

 顶点结构

 十字链表结构

边界点结构

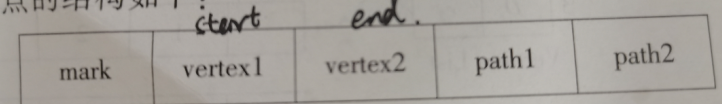
 顶点结构

 图的遍历

深度优先搜索

广度优先搜索

最小生成树

 各个节点进行连通，通过最小权值的边

两种算法：普利姆（prime）：选取顶点权值最小的那个边，重复这个过程，直到所有节点都加入

克鲁斯卡：选取所有剩余边权值最小的，重复这个过程，直到所有节点都加入

活动网络

AOV网络：有向图用顶点表示活动，用有向边<i,j>表示活动i先于活动j进行

拓扑排序：构造AOV顶点的拓扑有序序列的运算成为拓扑排序

AOE网络：无有向环的带权有向图，有向边表示工程的各个活动，权值表示活动时间，定点表示事件

关键路径：在AOE网络中，从源点（入度为0的定点）到汇点（出度为0）具有最大长度的路径成为关键路径

拓扑排序过程：（如果存在有向环，则会剩余些顶点）

1. 输入AOV网络；
2. 选择一个没有前趋节点的定点，并输出
3. 删除该顶点的所有边
4. 重复2和3

最短路径

迪杰斯特拉算法：贪心策略，按路径长度的递增次序逐步产生最短路径

弗洛伊德算法

七、查找

1、查找方法

顺序查找法：在线性表中进行查找

折半查找法，又称二分法

分块查找法：快与快之间必须进行排序（升序或是降序）。查找时，先通过索引表查找块，再在块中进行顺序查找。

2、二叉查找树与平衡二叉树

二叉查找树 相关定义：

1. 每个节点都有一个作为查找依据的关键码，所有节点的关键码互不相同
2. 若它的左子树不为空，则左子树上所有节点的关键码均小于根节点的关键码
3. 若它的右子树不为空，则右子树上所有节点的关键码均大于根节点的关键码
4. 它的左右子树也是二叉查找树

平衡二叉树：左右子树都是平衡二叉树，左右子树高度之差的绝对值不超过1

3、B树