https://blog.csdn.net/m0_37786651/article/details/61614865
从感知器谈起
对于典型的二分类问题,线性分类器的目的就是找一个超平面把正负两类分开。对于这个超平面,我们可以用下面的式子来表示,
感知器是最简单的一种线性分类器。用f(x)表示分类函数,感知器可以如下来表示。
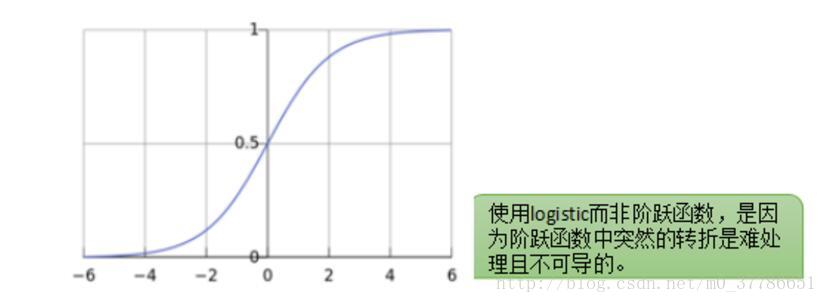
感知器相当于一个阶跃函数,如下图所示,在0处有一个突变。
损失函数是分类器优化的目标函数,可以用来衡量分类错误的程度,损失函数值越小,代表分类器性能越好。感知器的损失函数为误分类点的函数间隔之和,函数间隔可以理解为样本与分类超平面的距离。误分类点距离分类超平面越远,则损失函数值越大。只有误分类的点会影响损失函数的值。
从感知器到logistic回归
感知器模型简单直观,但问题在于这个模型不够光滑,比如如果对于一个新的样本点我们计算出ω^T x+b=0.001,只比0大了一点点就会被分为正样本。同时这个点在0处有一个阶跃,导致这一点不连续,在数学上处理起来不方便。
那有没有办法让 ωTx+bωTx+b 到y的映射变得更加光滑呢,人们发现logistic函数有着这样的特性,输入范围是−∞→+∞,而值域光滑地分布于0和1之间。于是就有了logistic回归,正样本点分类的超平面距离越远,ωTx+bωTx+b 越大,而logistic函数值则越接近于1。负样本点分类的超平面距离越远,ωTx+bωTx+b 越小,而logistic函数值则越接近于0。
Logistic回归的损失函数为logistic损失函数,当分类错误时,函数间隔越大,则损失函数值越大。当分类正确时,样本点距离超平面越远,则损失函数值越小。所有的样本点分布情况都会影响损失函数最后的值。
从感知器到SVM
在感知器分类选分类超平面时,我们可以选择很多个平面作为超平面,而选择哪个超平面最好呢,我们可以选择距离正样本和负样本最远的超平面作为分类超平面,基于这种想法人们提出了SVM算法。SVM的损失函数为合页函数,当分类错误时,函数间隔越大,则损失函数值越大。当分类正确且样本点距离超平面一定距离以上,则损失函数值为0。误分类的点和与分类超平面距离较近的点会影响损失函数的值。
感知器、logistic与SVM
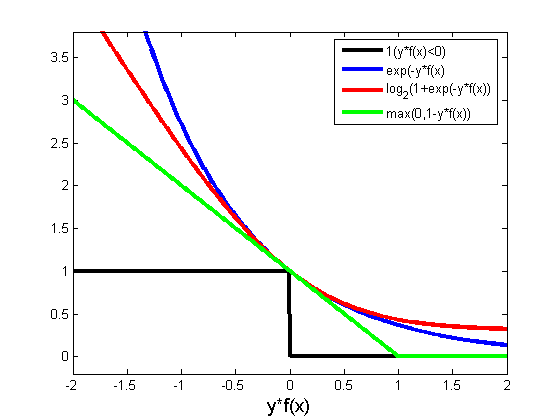
三者都是线性分类器,而logistic和svm是由感知器发展改善而来的。区别在于三者的损失函数不同,后两者的损失函数的目的都是增加对分类影响较大的数据点的权重,SVM的处理方法是只考虑support vectors,也就是和分类最相关的少数点,去学习分类器。而逻辑回归通过非线性映射,大大减小了离分类平面较远的点的权重,相对提升了与分类最相关的数据点的权重。下图中红色的曲线代表logistic回归的损失函数,绿色的线代表svm的损失函数。
参考
[1] 统计学习方法,李航
[2] http://blog.csdn.net/hel_wor/article/details/50539967
[3] https://www.zhihu.com/question/21704547