拉格朗日乘子法和KKT条件
1 无约束优化
对于无约束优化问题中,如果一个函数f是凸函数,那么可以直接通过f(x)的梯度等于0来求得全局极小值点。
为了避免陷入局部最优,人们尽可能使用凸函数作为优化问题的目标函数。
凸集定义:欧式空间中,对于集合中的任意两点的连线,连线上任意一点都在集合中,我们就说这个集合是凸集。
凸函数定义:对于任意属于[0,1]的a和任意属于凸集的两点x, y,有f( ax + (1-a)y ) <= a * f(x) + (1-a) * f(y),几何上的直观理解就是两点连线上某点的函数值,大于等于两点之间某点的函数值。凸函数的任一局部极小点也是全局极小点
半正定矩阵的定义:特征值大于等于0的实对称矩阵。
半正定矩阵的充要条件:行列式(n阶顺序主子式)等于0,行列式的i阶顺序主子式>=0,i从1到n-1
凸函数的充要条件:如果f(x)在开凸集S上具有二阶连续偏导数,且f(x)的海塞矩阵(二阶偏导的矩阵)在S上处处半正定,则f(x)为S上的凸函数。
2 约束优化定义
考虑带约束的优化问题,可以描述为如下形式
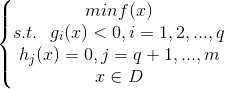
其中f(x)是目标函数,g(x)为不等式约束,h(x)为等式约束。
若f(x),h(x),g(x)三个函数都是线性函数,则该优化问题称为线性规划。若任意一个是非线性函数,则称为非线性规划。
若目标函数为二次函数,约束全为线性函数,称为二次规划。
若f(x)为凸函数,g(x)为凸函数,h(x)为线性函数,则该问题称为凸优化。注意这里不等式约束g(x)<=0则要求g(x)为凸函数,若g(x)>=0则要求g(x)为凹函数。
凸优化的任一局部极值点也是全局极值点,局部最优也是全局最优。
3 等式约束
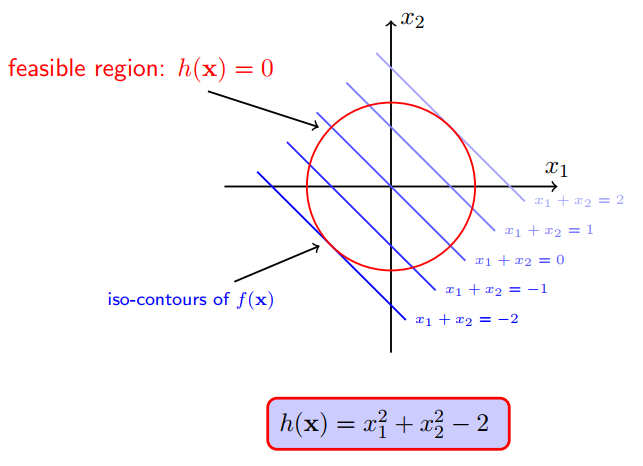
考虑一个简单的问题目标函数f(x) = x1 + x2,等式约束h(x)=x21+x22−2h(x)=x12+x22−2,求解极小值点。
f(x)在二维平面上画出等高线(contour)就是一条条斜率相同的直线,h(x)=0在二维平面上画出等高线就是一个圆,如下图所示。
可以明显的看出,在圆圈h(x)的限制下,直线f(x)的最小值为-2,在左下角直线x1+x2=2和圆的交点上。
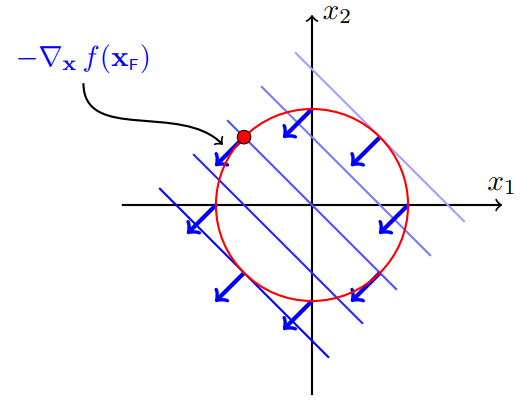
不考虑圆h(x)的限制时,f(x)要得到极小值,需要往f(x)的负梯度(下降最快的方向)方向走,如下左图蓝色箭头。
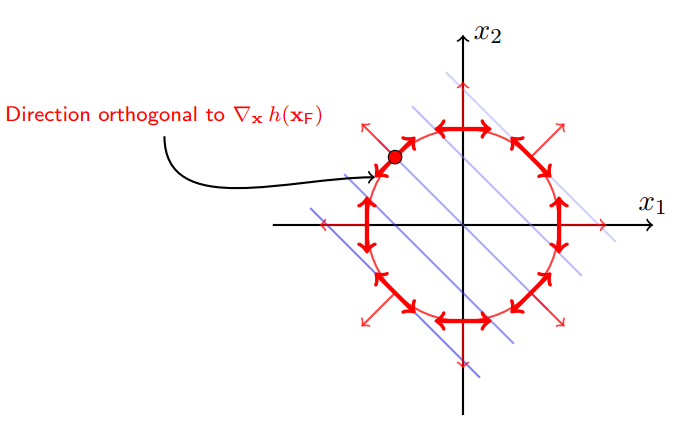
如果考虑圆h(x)的限制,要得到极小值,需要沿着圆的切线方向走,如下右图红色粗箭头。注意这里的方向不是h(x)的梯度,而是正交于h(x)的梯度,h(x)梯度如下右图的红色细箭头。
在极小值点,f(x)和h(x)的等高线是相切的。
容易发现,在关键的极小值点处,f(x)的负梯度和h(x)的梯度在同一直线上,如下图左下方critical point的蓝色和红色箭头所示。
注意图中所示是同向的,但是这里并不一定是同向,有可能反向(因为等式约束h(x)=0,把h(x)变成-h(x)求解是一样的,这个时候h(x)的梯度就相反了)
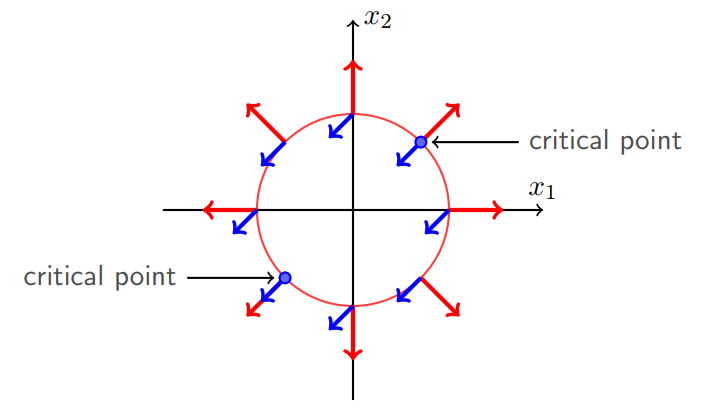
由此可知,在极小值点,h(x)和f(x)的梯度在同一线上,有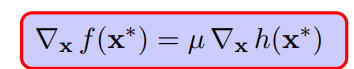
所以,对于f(x)和h(x)而言,只要满足上面这个式子,同时使得h(x) = 0,解得的x就是我们要求的极小值点(或极大值点,为了简单起见我们只讨论极小值点)
要做到这一点,可以构造一个拉格朗日函数,对函数令偏导等于0求解,恰好等价于“满足上面这个式子,同时使得h(x) = 0",原问题转化为对拉格朗日函数求极值问题,这就是拉格朗日乘子法,如下图所示(注意一下这个μ的正负变化)。

特别注意:优化问题是凸优化的话,通过上图两个条件求得的解就是极小值点(而且是全局极小)。
不是凸优化的话,这两个条件只是极小值点的必要条件,还需要附加多一个正定的条件才能变成充要条件,如下图所示。

4 不等式约束
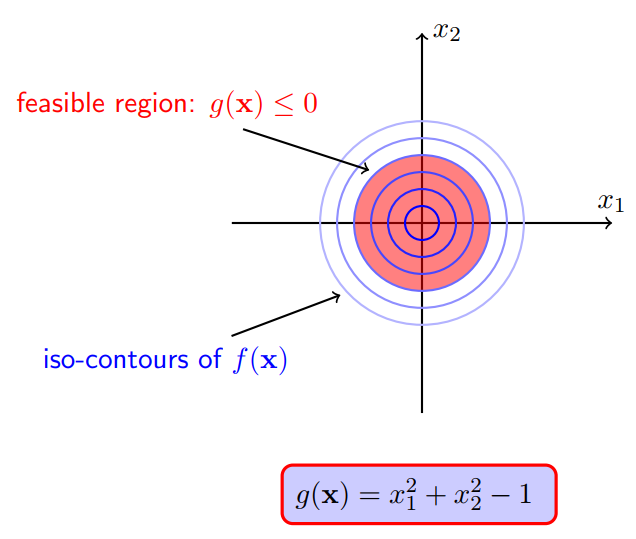
对于不等式约束g(x)<=0,和等式约束h(x)=0不一样,h(x)=0可以在平面上画出一条等高线,而g(x)<=0是一个区域,很多个等高线堆叠而成的一块区域,我们把这块区域称为可行域。
不等式约束分两种情况来讨论,第一种是(不考虑可行域限制时的)极小值点落在可行域内(不包含边界),第二种是(不考虑可行域限制时的)极小值点落在可行域外(包含边界)。
下面举两个例子来解释这两种情况,然后总结两种情况给出转换求解。
4.1 极小值点落在可行域内(不包含边界)
考虑目标函数f(x)=x21+x22f(x)=x12+x22,不等值约束g(x)=x21+x22−1g(x)=x12+x22−1,显然f(x)的极小值为原点(0,0),落在可行域内。可行域以原点为圆心,半径为1。
这种情况约束不起作用,考虑极小值点x*,这个时候,g(x*) < 0,f(x*)的梯度等于0。
4.2 极小值点落在可行域外(包含边界)
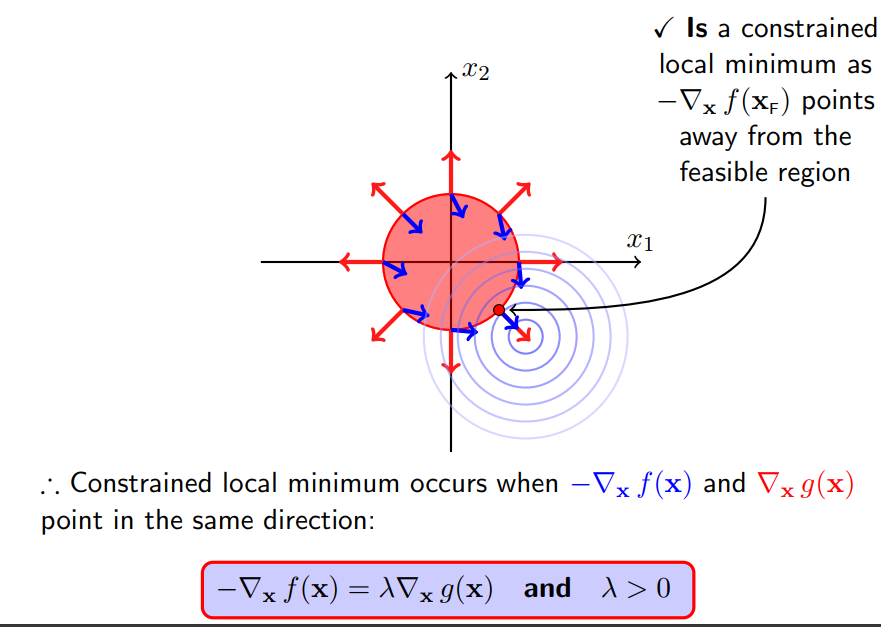
考虑目标函数f(x)=(x1−1.1)2+(x2+1.1)2f(x)=(x1−1.1)2+(x2+1.1)2 ,不等值约束g(x)=x21+x22−1g(x)=x12+x22−1,显然f(x)的极小值为原点(1.1, -1.1),落在可行域外。可行域以原点为圆心,半径为1。
这种情况约束起作用,要考虑求解f(x)在可行域内的极小值点。
对于f(x)而言要沿着f(x)的负梯度方向走,才能走到极小值点,如下图的蓝色箭头。
这个时候g(x)的梯度往区域外发散,如下图红色箭头。
显然,走到极小值点的时候,g(x)的梯度和f(x)的负梯度同向。因为极小值点在边界上,这个时候g(x)等于0。
4.3 总结
极小值点落在可行域内(不包含边界):这个时候可行域的限制不起作用,相当于没有约束,直接f(x)的梯度等于0求解,这个时候g(x极小值点)<0(因为落在可行域内)。
极小值点落在可行域外(包含边界):可行域的限制起作用,极小值点应该落在可行域边界上即g(x)=0,类似于等值约束,此时有g(x)的梯度和f(x)的负梯度同向。

总结以上两种情况,可以构造拉格朗日函数来转换求解问题。
对于不等式约束的优化,需要满足三个条件,满足这三个条件的解x*就是极小值点。
这三个条件就是著名的KKT条件,它整合了上面两种情况的条件。
特别注意:优化问题是凸优化的话,KKT条件就是极小值点(而且是全局极小)存在的充要条件。
不是凸优化的话,KKT条件只是极小值点的必要条件,不是充分条件,KKT点是驻点,是可能的极值点。也就是说,就算求得的满足KKT条件的点,也不一定是极小值点,只是说极小值点一定满足KKT条件。

不是凸优化的话,还需要附加多一个正定的条件才能变成充要条件,如下图所示。

5 约束优化总结
拓展一下,对于同时有多个等式约束和多个不等式约束,构造的拉格朗日函数就是在目标函数后面把这些约束相应的加起来,KKT条件也是如此,如下图所示。

6 优化问题的总结
简单总结一下,考虑凸优化问题。
对于无约束的优化问题,直接令梯度等于0求解。
对于含有等式约束的优化问题,拉格朗日乘子法,构造拉格朗日函数,令偏导为0求解。
对于含有不等式约束的优化问题,同样构造拉格朗日函数,利用KKT条件求解。
对于含有约束的优化问题,还可以转化为对偶问题来求解,下篇讲述一下拉格朗日对偶性的问题http://www.cnblogs.com/liaohuiqiang/p/7805954.html。
7 参考资料
瑞典皇家理工学院(KTH)“统计学习基础”课程的KKT课件:http://www.csc.kth.se/utbildning/kth/kurser/DD3364/Lectures/KKT.pdf
这门“统计学习基础”的schedule上有一些其它课件:http://www.csc.kth.se/utbildning/kth/kurser/DD3364/Schedule.php