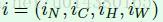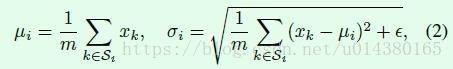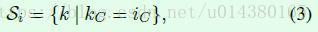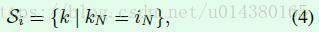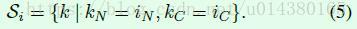Group Normalization算法笔记
论文:Group Normalization
论文链接:https://arxiv.org/abs/1803.08494
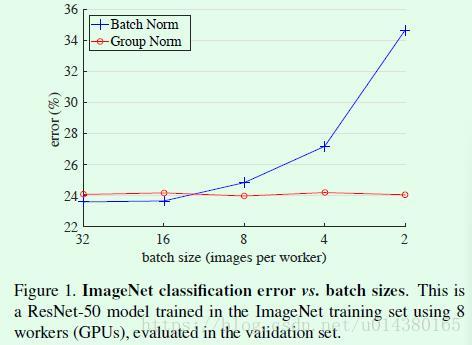
Group Normalization(GN)是针对Batch Normalization(BN)在batch size较小时错误率较高而提出的改进算法,因为BN层的计算结果依赖当前batch的数据,当batch size较小时(比如2、4这样),该batch数据的均值和方差的代表性较差,因此对最后的结果影响也较大。如图Figure1所示,随着batch size越来越小,BN层所计算的统计信息的可靠性越来越差,这样就容易导致最后错误率的上升;而在batch size较大时则没有明显的差别。虽然在分类算法中一般的GPU显存都能cover住较大的batch设置,但是在目标检测、分割以及视频相关的算法中,由于输入图像较大、维度多样以及算法本身原因等,batch size一般都设置比较小,所以GN对于这种类型算法的改进应该比较明显。
因此Group Normalization(GN)的思想并不复杂,简单讲就是要使归一化操作的计算不依赖batch size的大小,原文的这段话概括得非常好:GN divides the channels into groups and computes within each group the mean and variance for normalization. GN’s computation is independent of batch sizes, and its accuracy is stable in a wide range of batch sizes.
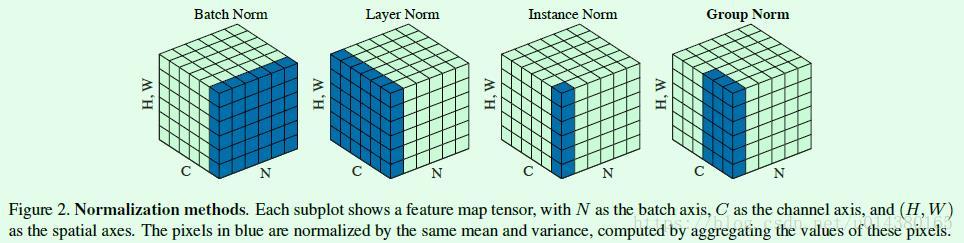
Figure2是几种归一化方式的对比(Bartch Norm、Layer Norm、Instance Norm和Group Norm),可以一并回顾下BN算法。Figure2中的立方体是三维,其中两维C和N分别表示channel和batch size,第三维表示H,W,可以理解为该维度大小是H*W,也就是拉长成一维,这样总体就可以用三维图形来表示。可以看出BN的计算和batch size相关(蓝色区域为计算均值和方差的单元),而LN、BN和GN的计算和batch size无关。同时LN和IN都可以看作是GN的特殊情况(LN是group=1时候的GN,IN是group=C时候的GN)。
接下来看看Figure2中提到的四种归一化方式的公式计算。首先常见的特征归一化算法(BN,LN,IN,GN)基本上都如公式1+公式6所示。公式1是减均值并除以标准差的操作,公式6是一个线性变换。 
xi中i的含义如下,其实就是四个维度的坐标,这样xi就是feautre map中指定位置的一个点。
公式1中的均值和标准差的计算公式如公式2所示:
到目前为止的公式都是常规的归一化操作公式,而BN、LN、IN和GN的差别就在于公式2中集合Si的范围。比如BN中Si如公式3所示。iC和kC都表示channel,Si表示计算均值和标准差的点集合,k表示在kC=iC情况下的四维点坐标。举个例子,假设要计算公式1的点的iC是3,那么从公式3来看,只有kC=3的点(xk)构成的集合Si才参与计算均值和方差,换句话说就是相同通道的点才参与计算当前点的均值和标准差。
同理,LN中Si如公式4所示,换句话说就是相同feature map(N这个维度)的点才参与计算当前点的均值和标准差,这样计算均值和方差就和batch size无关,参看Figure2。
IN的Si如公式5所示,换句话说就是相同通道且相同feature map(N这个维度)的点才参与计算当前点的均值和标准差,同样计算均值和方差和batch size无关,参看Figure2。
GN的Si如公式7所示,首先kN=iN使得计算都是在一张图的feature map上进行,G表示将C分成G个group,因此G是一个超参数,默认设置为32。 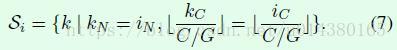
而公式7中的如下等式表示在同一个group中的点。 
因此GN的思想就是在相同feature map的相同group中进行归一化操作,而group只是在channel维度上进行划分,因此归一化操作就和batch size无关。
TensorFlow框架下GroupNorm的Python实现代码如截图函数所示。先将维度C reshape成两个维度(G和C//G),然后计算mean和var的时候基于维度C//G、H和W,最后将维度reshape回原来的4维并返回线性变换后的结果。
实验结果:
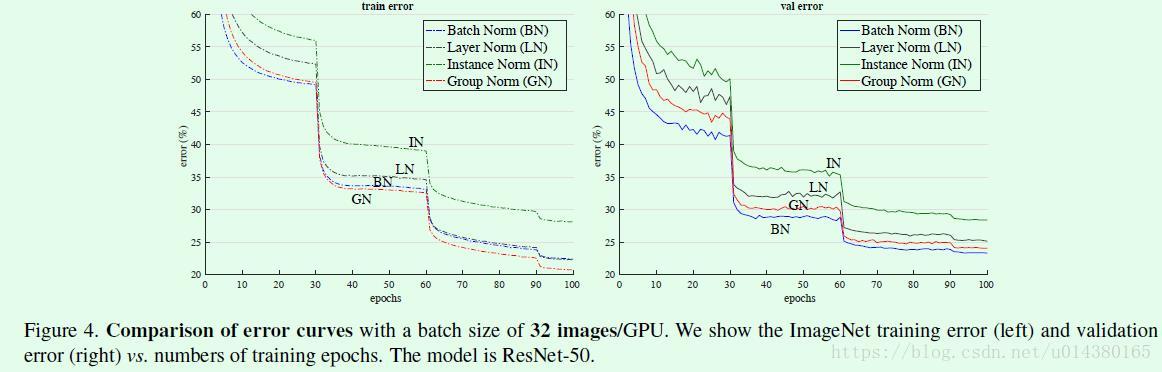
Figure4是对比几种不同归一化算法在ImageNet数据集上batch size设置为32时的训练和验证误差。可以看出在训练时候GN的表现要优于BN,但是在验证时却要比BN差一些。
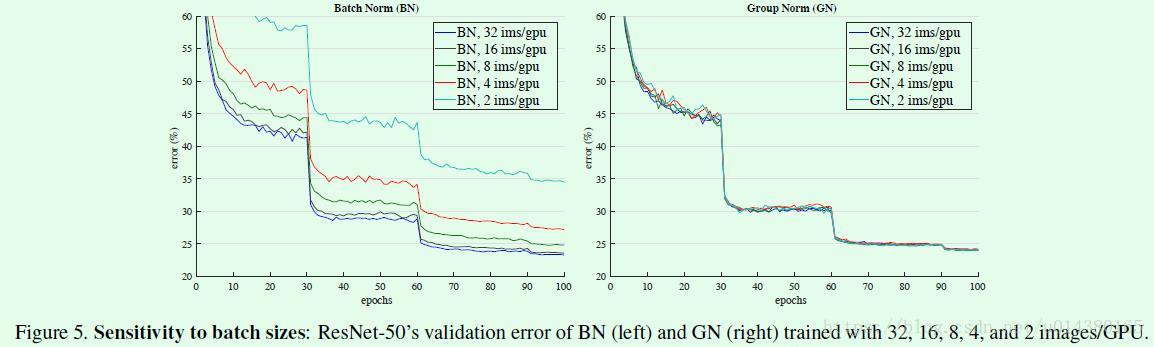
Figure5是验证batch size大小分别对BN和GN的影响。可以看出GN基本上不受batch size的影响。