poj 1390 Blocks

Time Limit: 5000MS             Memory Limit: 65536K
Total Submissions: 6528        Accepted: 2697

Description

Some of you may have played a game called 'Blocks'. There are n blocks in a row, each box has a color. Here is an example: Gold, Silver, Silver, Silver, Silver, Bronze, Bronze, Bronze, Gold. 
The corresponding picture will be as shown below: 

 

Figure 1

If some adjacent boxes are all of the same color, and both the box to its left(if it exists) and its right(if it exists) are of some other color, we call it a 'box segment'. There are 4 box segments. That is: gold, silver, bronze, gold. There are 1, 4, 3, 1 box(es) in the segments respectively. 

Every time, you can click a box, then the whole segment containing that box DISAPPEARS. If that segment is composed of k boxes, you will get k*k points. for example, if you click on a silver box, the silver segment disappears, you got 4*4=16 points. 

Now let's look at the picture below: 

Figure 2

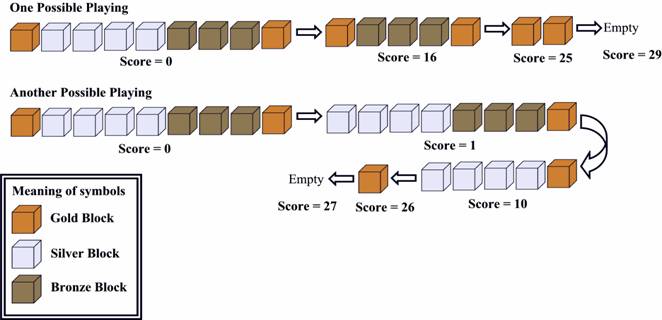
The first one is OPTIMAL. 

Find the highest score you can get, given an initial state of this game. 

Input

The first line contains the number of tests t(1<=t<=15). Each case contains two lines. The first line contains an integer n(1<=n<=200), the number of boxes. The second line contains n integers, representing the colors of each box. The integers are in the range 1~n.

Output

For each test case, print the case number and the highest possible score.

Sample Input

2
9
1 2 2 2 2 3 3 3 1
1
1

Sample Output

Case 1: 29
Case 2: 1

解题思路：

此题是训练递归算法的一道非常好的题目，本来以为很简单，但是发现实现起来难度颇大，最后还是变成了阅读大佬代码orz。

本题的关键点是确定dp表达式，将问题转化为求解(l,r)区间上的最大分值，但是很明显在祖玛块消解过程中，右端可能会出现颜色一样的块，所以也要考虑在内。（为什么不考虑左端，是因为左端放在表达式中另外考虑了）

所以考虑函数f(l,r,len)，表示与r位同色的右边还有len个情况下，(l,r)区间上的最大分数。

最右边处理有两种策略，第一种是直接消去，第二种是和左边另一个同色块合并后再消去。对应dp状态转移方程式：
f(l,r,len)=max{f(l,r-1,0)+(num[r]+len)*(num[r]+len),f(l,k,len+num[r])+f(k+1,r-1,0)(l<=k<=r-2 && c[k]==c[r])}

注意事项：

1.一开始应该预处理令相邻同色块合并成一个大块，用num[i],c[i]，记录大块中色块数目与颜色，用于减少搜索过程中对相邻同色块的搜索。 
2.边界条件为l==r时直接处理，可以节省一次递归：l==r时f(l,r,len)=(num[r]+len)*(num[r]+len)。
3.用max数组存储分数，避免重复计算（对应TLE）。

AC代码：

#define MAX_N 200

#include<stdio.h>
#include<memory.h>

int cases,n,m;
int color[MAX_N+1];
int num[MAX_N+1],c[MAX_N+1];
int max[MAX_N+1][MAX_N+1][MAX_N+1];

int f(int l,int r,int len)
{ 
    if (l==r)
        return max[l][r][len]=(num[r]+len)*(num[r]+len);
    if (max[l][r][len])
        return max[l][r][len];
    int temp=f(l,r-1,0)+(len+num[r])*(len+num[r]);
    for (int k=l;k<r;k++)
        if (c[k]==c[r]) 
            if (f(l,k,num[r]+len)+f(k+1,r-1,0)>temp)
                temp=f(l,k,num[r]+len)+f(k+1,r-1,0);
    return max[l][r][len]=temp;
}

int main()
{
    scanf("%d",&cases);
    color[0]=0;
    for (int loop=1;loop<=cases;loop++)
    {
        memset(max,0,sizeof(max));
        scanf("%d",&n);
        m=0;
        for (int i=1;i<=n;i++)
        {
            scanf("%d",&color[i]);
            if (color[i]==color[i-1])
                num[m]++;
            else
            {
                m++;
                c[m]=color[i];
                num[m]=1;
            }
        }
        printf("Case %d: %d
",loop,f(1,m,0));
    }
    return 0;
}

参考网址：

https://blog.csdn.net/PKU_ZZY/article/details/51442591