1.已知一棵深度为k的树中有n1个度为1的结点,n2个度为2的结点,…,nk个度为k的结点,问该树中有多少个叶子结点?
(前提:
对任何一个二叉树,若齐叶子结点数为n0,度为2的结点数为n2,则n0=n2+1。证明如下:
设一颗二叉树上叶子结点数为n0,单分支结点数为n1,双分支结点数为n2,则总结点数为:n0+n1+n2。
而一颗二叉树中,所有结点的分支数(即度数)应等于单分支结点数加上双分支结点数的两倍,即总分支数=n1+2n2。
由于二叉树中除了根结点以外,每个结点都有唯一的一个分支指向它,因此二叉树中:总分支数=总结点数-1。
即n1+2n2=n0+n1+n2-1。即n0=n2+1。)
 是乘号哦
是乘号哦
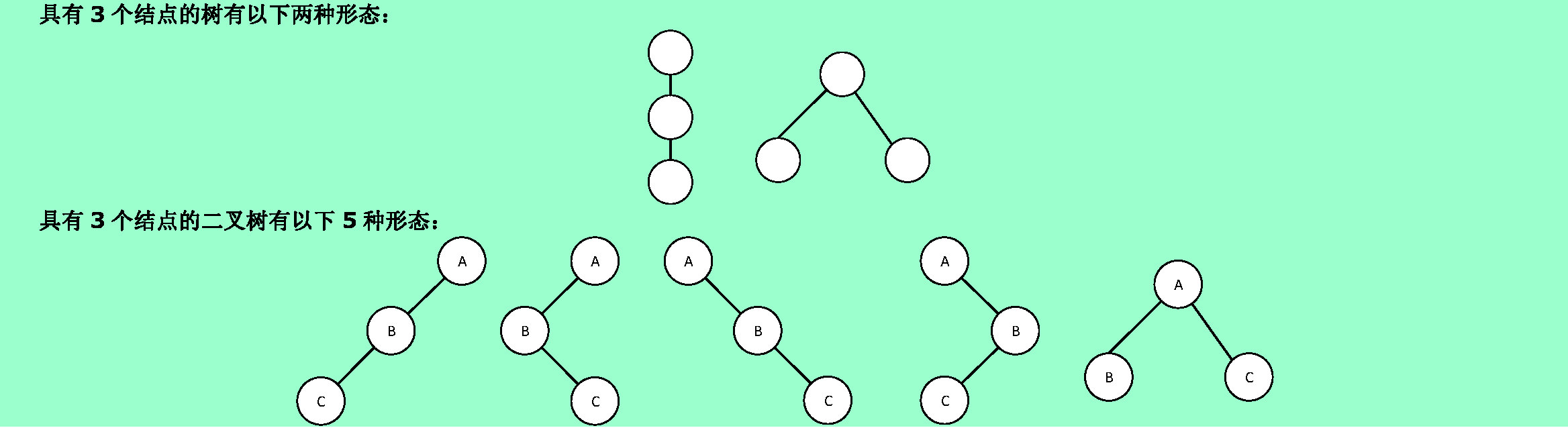
2.试分别画出具有3个结点的树和3个结点的二叉树的所有不同形态。
3.树的同构

4.算术式的二叉树表示:当我们对此二叉树进行先序、中序和后序遍历后,便可得到表达式的前缀、中缀和后缀
(a+b×(c-d))-e/f

运算符在树中放在非终端结点的位置上,操作数放在叶子结点处
前缀:-+a*b-cd/ef (波兰表达式)
中缀:a+b*c-d-e/f
后缀:abcd-*+ef/- (逆波兰表达式)
其中,中缀形式是算术表达式的通常形式,只是没有括号。在计算机内,使用后缀表达式易于求值。
5.

6.编写递归算法:对于二叉树中每一个元素值为x的节点,删去以它为跟的子树,并释放响应的空间
(转自大神:https://wenku.baidu.com/view/c0f2be04eff9aef8941e06c2.html)
1 /* 2 输入样例: 3 1 4 124###3## 5 6 2 7 124###3## 8 9 2 10 123##4##537##8### 11 */ 12 #include <bits/stdc++.h> 13 using namespace std; 14 typedef struct node { 15 char data; 16 struct node *lchild; 17 struct node *rchild; 18 } *Bitree; 19 char ch; 20 Bitree root, pre; 21 Bitree CreateBitree() { 22 cin >> ch; 23 Bitree T; 24 T = new node; 25 if(ch == '#') T = NULL; 26 //注意:二叉树的输入需要严格遵守以#结尾的规则,并且输入顺序按照前序遍历的方式 27 else { 28 T->data = ch; 29 T->lchild = CreateBitree(); 30 T->rchild = CreateBitree(); 31 } 32 return T; 33 } 34 35 void Remove(Bitree T) {//删除以T为根节点的树 36 37 if(T) { 38 Remove(T->lchild); 39 Remove(T->rchild); 40 } 41 42 delete T;//delete删除的是T指向的空间,而不是T本身 43 44 } 45 46 void print(Bitree T) {//前序遍历打印 47 if(T) { 48 cout << T->data << " "; 49 print(T->lchild); 50 print(T->rchild); 51 } 52 } 53 54 void Pre(Bitree T, char x, Bitree pre) { 55 if(T) {//删除有两件事的 既要把自己的树删掉 也要防止父节点指针悬空乱指 56 if(T->data == x && T != root) { //如果删除的不是根节点 57 if(pre->lchild == T) pre->lchild = NULL;//防止删除节点的父节点的指针悬空 58 else if(pre->rchild == T) pre->rchild = NULL; 59 Remove(T); 60 return; 61 62 } 63 else if(T->data==x)Remove(T);//如果删除的是根节点 64 Pre(T->lchild, x, T);//这里保证了第三个参数是第一个节点的父节点 也就是pre->child==T 65 Pre(T->rchild, x, T); 66 } 67 } 68 69 char dele; 70 int main() { 71 cin >> dele;//输入要删除的数值 72 root = CreateBitree();//建树 73 print(root);//前序遍历打印树 74 // pre = NULL; 75 Pre(root, dele, root);//进行删除操作,输入分别代表根节点,要删除的数值,当前节点的父节点 76 printf(" ________ "); 77 if(dele==root->data) printf("NULL ");//如果当前删除的是根节点那么输出NULL 因为此时就进不去print的if函数了 78 else print(root);//如果不是根节点,就按照前序遍历输出这棵树 79 return 0; 80 }