一、K-近邻算法原理
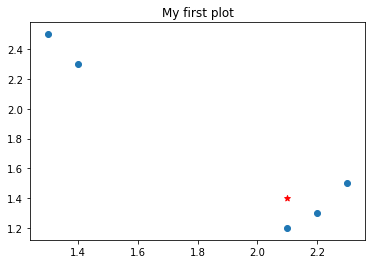
如图所示,数据表中有两个属性,两个标签(A,B),预测最后一行属于哪种标签。
| 属性一 | 属性二 | 标签 |
| 2.1 | 1.2 | A |
| 1.3 | 2.5 | B |
| 1.4 | 2.3 | B |
| 2.2 | 1.3 | A |
| 2.3 | 1.5 | A |
| 2.1 | 1.4 | ? |
通过可视化数据,可以看到A和B分别集中某一领域,观察可见,第六行(2.1,1.4)比较靠近标签A。
K-近邻原理:因为未知标签的属性是已知的,可以通过计算未知标签的属性与已知标签的属性的距离,参数K表示最近邻居的数目,如当K=3,即取最近的三个距离值,通过概率论,三个之中哪个标签占的概率高就代表,未知标签就是等同此标签。
公式: ![]()
例如:点(1,0)与(2.3)之间的距离计算为:
((1-0)^2 +(2-3)^2)再开方
《机器学习实战》这本书原话:
对未知类别属性的数据集中的每个点依次执行以下操作:
(1) 计算已知类别数据集中的点与当前点之间的距离;
(2) 按照距离递增次序排序;
(3) 选取与当前点距离最小的k个点;
(4) 确定前k个点所在类别的出现频率;
(5) 返回前k个点出现频率最高的类别作为当前点的预测分类。
二、代码处理K-近邻算法步骤
1 import numpy as np #导入numpy模块 2 import operator as op #导入operator模块 3 import operator 4 5 6 #生成训练数据函数 7 def createDataSet(): 8 dataSet = np.array([[2.1,1.2],[1.3,2.5],[1.4,2.3],[2.2,1.3],[2.3,1.5]]) #数据集的规模是四行两列的数组 9 labels = ['A','B','B','A','A'] #数据集每一条记录所对应的标签 10 return dataSet, labels #返回数据集数据和它对应的标签
#K-NN预测分类函数 #inX:一条未知标签的数据记录 #dataSet:训练数据集 #labels:训练数据集每一条记录所对应的标签 #k:事先人为定义的数值 def classify0(inX, dataSet, labels, k): #获取数据集的行数或者记录数,.shape[0]:获取矩阵的行数,.shape[1]:获取数据集的列数 dataSetSize = dataSet.shape[0] #将修改规模后的未知标签的数据记录与训练数据集作差 diffMat = np.tile(inX, (dataSetSize,1)) - dataSet #再将对应得到的差值求平方 sqDiffMat = diffMat**2 #横向求得上面差值平方的和,axis=1:表示矩阵的每一行分别进行相加 sqDistances = sqDiffMat.sum(axis=1) #再对每条记录的平方和开方,得到每一条已知标签的记录与未知标签数据的距离 distances = sqDistances**0.5 #对求得的距离进行排序,返回的是排序之后的数值对应它原来所在位置的下标 sortedDistIndicies = distances.argsort() #创建一个空的字典,用来保存和统计离未知标签数据最近的已知标签与该标签的个数,标签作为字典的key(键),该标签的个数作为字典的value(值) classCount={} for i in range(k): #sortedDistIndicies[i]排序之后得到的k个离未知标签数据最近的训练数据记录下标,比如是第二条记录,那它就等于1(下标从零开始) #voteIlabel就是:训练数据第sortedDistIndicies[i]条记录的标签 voteIlabel = labels[sortedDistIndicies[i]] #把上面得到的那个标签作为字典的键,并且累计k个标签中,该标签有多少个,这个累计个数作为该标签的键值,也就是value classCount[voteIlabel] = classCount.get(voteIlabel,0) + 1 #对上面循环得到的标签统计字典进行按值(标签的累计数)排序,并且是从大到小排序 #下面的写法是固定的 #classCount.items():得到字典的键和值两个列表 #key=operator.itemgetter(1):指明该排序是按字典的值从小到大排序,与键无关 #reverse=True:从大到小排序 sortedClassCount = sorted(classCount.items(), key=operator.itemgetter(1), reverse=True) #统计数最大的那个标签,作为对未知标签的预测,也就是该返回标签就是未知标签数据inX的预测标签了 return sortedClassCount[0][0]
#填写一个预测属性值,输出属性对应的标签 aa = classify0([1.2,2.3], dataSet, labels, 3) print(aa)
以上就是简单的K-近邻算法的理论原理和代码实现过程
以上就是我的拙见,非常感谢您能看到这里,有什么问题可以评论指正哦。