2Improved neural networks
2.1深度学习使用层面
2.1.1正则化可以减小过拟合
正则化为什么可以减小overfitting?
因为添加lambda parameters以后,在z不变情况下,WL*A[L-1]相对就减小,缩小到线性区域后,z近似于linear,所以classification趋向于平滑,不像一开始的overfitting

权重衰减的作用:权重衰减 == L2正则化
reduce variance的作用:reduce variance = reduce overfitting
keep_prob的作用:keep_prob为0,等于所有神经元失活
使用Dropout:
- 关闭dropout功能,即设置 keep_prob = 1.0;
- 运行代码,确保J(W,b)函数单调递减;
- 再打开dropout函数。
所以在测试(调试)阶段,应当关掉dropout功能,此时也不需要保留1/keep_prob因子
data augmentation的作用:为了防止模型过拟合,数据增强也是一种非常有效的方法,好多牛逼的模型除了网络结构精妙意外,在数据(比较吃数据的有监督深度学习)上也做了不可忽视的工作,才有state of the art的效果
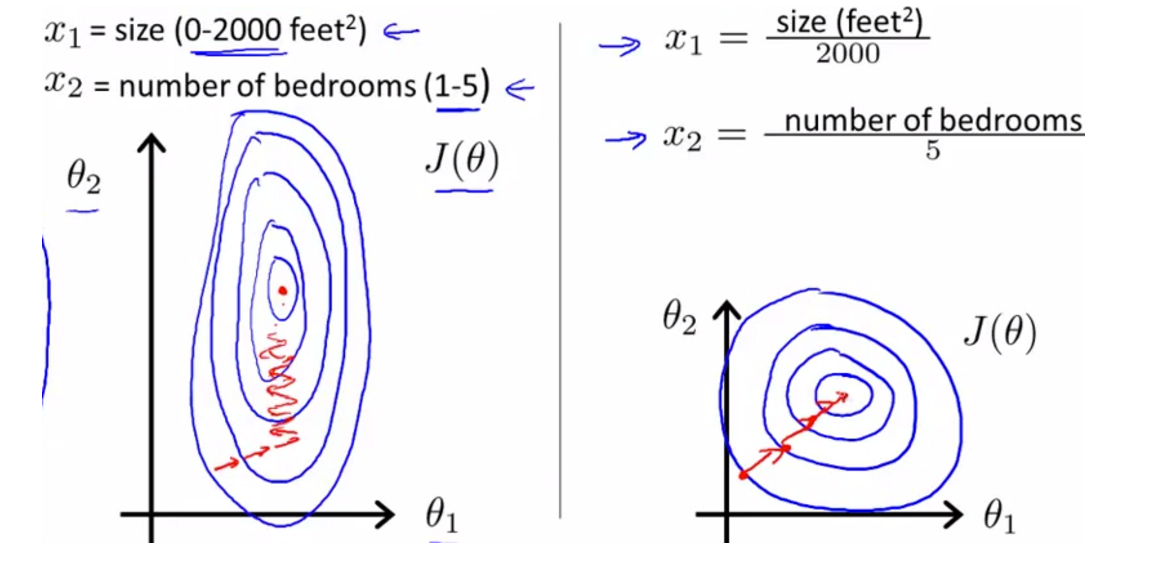
归一化的作用:数据归一化后,最优解的寻优过程明显会变得平缓,更容易正确的收敛到最优解。normalization可以加快网络收敛的速度,同时避免数值问题。
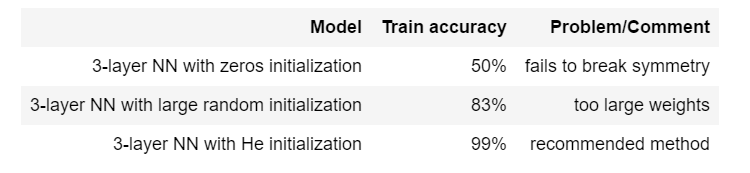
2.1.2三种初始化方法的总结
- 3-layer NN with zeros initialization
- 3-layer NN with large random initialization
- 3-layer NN with He initialization
求样本梯度
dWL = (1/m) * np.dot(dZ(L-1), AL.T)
2.2optimization
2.2.1expotentially weighted averages
![]()
计算权重平均
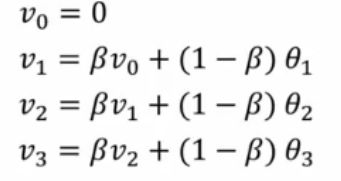
指数加权平均的修正误差
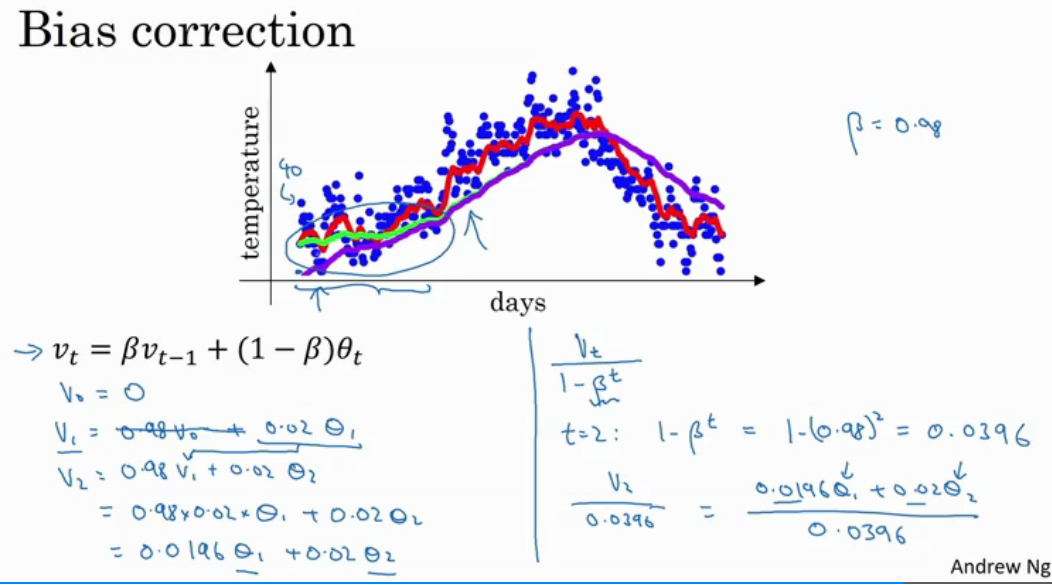
v_t可近似代表1/(1-β)个θ的平均值
上面这张图表明Vt = beta * Vt-1 + (1-beta) * theta_t在某种程度上就等于Vt / (1- beta^t),当iteration趋向于无穷大时候,vt 就趋向于1/3
偏差修正可以对加权平均做出调整,一般取
v0 = 0
v1 = beta * v0 + (1-beta) * theta_t
v2 = beta * v1 + (1-beta) * theta_t
...
数值偏小,前期与计算值有较大偏差,需要进行偏差修正 vt / (1-beta^t)

2.2.2gradient descent with momentum
momentum算法

总结:对于某些参数可能合适,对另外一些参数可能偏小(学习过程缓慢),对另外一些参数可能太大(无法收敛,甚至发散),而学习率一般而言对所有参数都是固定的,所以无法同时满足所有参数的要求。通过引入Momentum可以让那些因学习率太大而来回摆动的参数,梯度能前后抵消,从而阻止发散。
2.2.3RMSprop
RMSprop算法
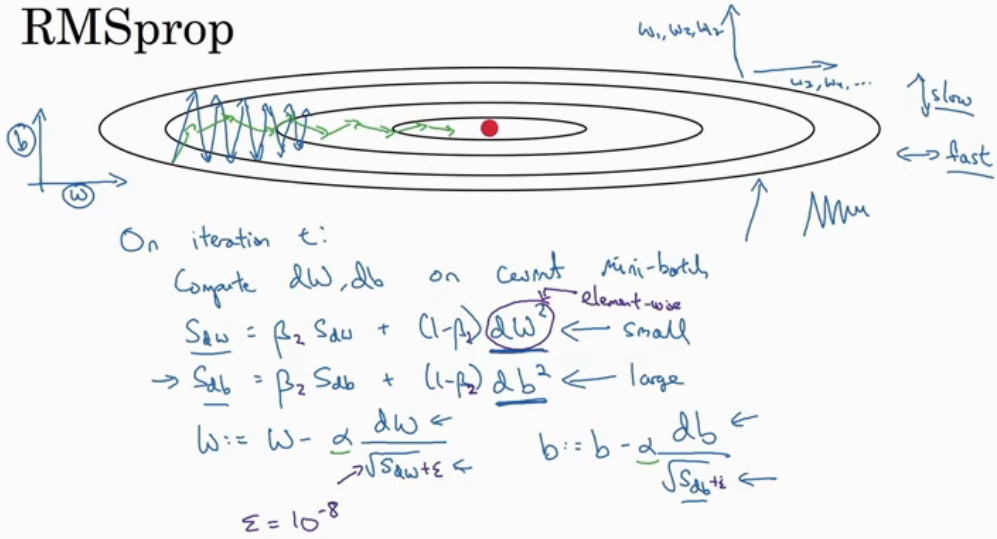
ADAM优化算法
ADAM算法本质是将Momentum和RMSprop结合起来

除了算法用作延误学习率外,其他也有一些延误学习率的方法

2.2.4assignment for optimization
当输入从第八个mini-batch的第七个的例子的时候,你会用哪种符号表示第三层的激活?
a[3]{8}(7)
注:[i]{j}(k)上标表示 第i层,第j小块,第k个示例
- 关于振荡模型


beta越小,振荡越多
增加beta,模型右移动
- 关于使用样例数方面
SGD使用 one training example
GD使用 the whole batch
2.3深度学习框架
