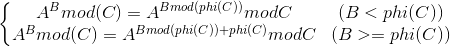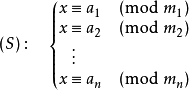点击查看数论基础知识
威尔逊定理给出了判定一个自然数是否为素数的充分必要条件 。但是由于阶乘是呈爆炸增长的,其结论对于实际操作意义不大。
当且仅当p为素数时,( p -1 )! ≡ -1 ( mod p )
当且仅当p为素数时,( p -1 )! ≡ p-1 ( mod p )
若p为质数,则p能被(p-1)!+1整除
当且仅当p为素数时,p∣(p−1)!+1
hdu 2973 YAPTCHA
题解分析
若n,a为正整数,且n,a互质,即gcd(a,n) = 1,则a φ ( n ) ≡ 1 ( m o d n ) a^{φ(n)} ≡ 1 (modspace n) a φ ( n ) ≡ 1 ( m o d n )
将欧拉定理拓展到A和C不互质的情况:
例1: (验证定理是否与结果相符)a φ ( n ) a^{φ(n)} a φ ( n ) 3 4 3^4 3 4 81 = 80 + 1 ≡ 1 ( m o d 5 ) space81=80+1equiv1(modspace5) 8 1 = 8 0 + 1 ≡ 1 ( m o d 5 )
例2: (实现简化幂的模运算)7 222 7^{222} 7 2 2 2 解: 7 222 7^{222} 7 2 2 2 7 4 ≡ 1 ( m o d 10 ) 7^4equiv1(modspace10) 7 4 ≡ 1 ( m o d 1 0 ) ∴ herefore ∴ 7 222 ( m o d 10 ) = [ ( 7 4 ) 55 ∗ ( 7 2 ) ] ( m o d 10 ) = [ ( 7 4 ) 55 ( m o d 10 ) ] ∗ [ ( 7 2 ) ( m o d 10 ) ] = 1 55 ∗ [ 7 2 ( m o d 10 ) ] = 49 ( m o d 10 ) = 9 ( m o d 10 ) �egin{aligned} 7^{222}(modspace10)&=[(7^4)^{55}*(7^2)](modspace10)\
&=[(7^4)^{55}(modspace10)]*[(7^2)(modspace10)]\
&=1^{55}*[7^2(modspace10)]\
&=49(modspace10)\
&=9(modspace10)end{aligned} 7 2 2 2 ( m o d 1 0 ) = [ ( 7 4 ) 5 5 ∗ ( 7 2 ) ] ( m o d 1 0 ) = [ ( 7 4 ) 5 5 ( m o d 1 0 ) ] ∗ [ ( 7 2 ) ( m o d 1 0 ) ] = 1 5 5 ∗ [ 7 2 ( m o d 1 0 ) ] = 4 9 ( m o d 1 0 ) = 9 ( m o d 1 0 ) 7 222 7^{222} 7 2 2 2
总结: 利用欧拉定理来简化幂模运算:a x ≡ a x % φ ( m ) ( m o d m ) a^x≡a^{x\%φ(m)}(modspace m) a x ≡ a x % φ ( m ) ( m o d m )
hdu 1395 2^x(mod n) = 1
题解分析
对 任 意 a 和 任 意 质 数 p , 有 a p ≡ a ( m o d p ) 对任意a和任意质数p,有a^pequiv a(modspace p) 对 任 意 a 和 任 意 质 数 p , 有 a p ≡ a ( m o d p )
对 任 意 a 和 任 意 质 数 p , 当 a 与 p 互 质 时 , 有 a p − 1 ≡ 1 ( m o d p ) 对任意a和任意质数p,当a与p互质时,有a^{p-1}equiv 1(modspace p) 对 任 意 a 和 任 意 质 数 p , 当 a 与 p 互 质 时 , 有 a p − 1 ≡ 1 ( m o d p )
若 p 能 被 a 整 除 , 则 a p − 1 ≡ 0 ( m o d p ) 若p能被a整除,则a^{p-1} ≡0(modspace p) 若 p 能 被 a 整 除 , 则 a p − 1 ≡ 0 ( m o d p )
计算 2 100 2^{100} 2 1 0 0
设a=2,p=13,正好满足gcd(a,p)=1。可以利用费马小定理:a p − 1 ≡ 1 ( m o d p ) a^{p-1}equiv 1(modspace p) a p − 1 ≡ 1 ( m o d p )
∴ 2 13 − 1 = 1 ( m o d 13 ) ⇒ 2 12 = 1 ( m o d 13 ) herefore 2^{13-1}=1(modspace 13)Rightarrow2^{12}=1(modspace 13) ∴ 2 1 3 − 1 = 1 ( m o d 1 3 ) ⇒ 2 1 2 = 1 ( m o d 1 3 )
解:
2 100 ( m o d 13 ) = 2 12 × 8 + 4 ( m o d 13 ) = [ ( 2 12 ) 8 ⋅ 2 4 ] ( m o d 13 ) = [ ( 2 12 ) 8 ( m o d 13 ) ] ⋅ [ 2 4 ( m o d 13 ) ] = 1 8 ⋅ [ 16 ( m o d 13 ) ] = 3 �egin{aligned} 2^{100}(modspace 13)&=2^{12 imes8+4}(modspace 13)\
&=[(2^{12})^8cdot2^4](modspace 13)\
&=[(2^{12})^8(modspace 13)]cdot[2^4(modspace 13)]\
&=1^8cdot[16(modspace 13)]\
&=3end{aligned} 2 1 0 0 ( m o d 1 3 ) = 2 1 2 × 8 + 4 ( m o d 1 3 ) = [ ( 2 1 2 ) 8 ⋅ 2 4 ] ( m o d 1 3 ) = [ ( 2 1 2 ) 8 ( m o d 1 3 ) ] ⋅ [ 2 4 ( m o d 1 3 ) ] = 1 8 ⋅ [ 1 6 ( m o d 1 3 ) ] = 3
hdu 4196 Remoteland
题解分析
中国剩余定理说明:假设整数m1,m2, … ,mn两两互质,则对任意的整数:a1,a2, … ,an,方程组S有解,并可构造得出。
中国剩余定理的孙子解法并没有什么高深的技巧,就是以下两个基本数学定理的灵活运用:
如果 a%b=c , 则有 (a+kb)%b=c (k为非零整数)。
如果 a%b=c,那么 (a*k)%b=kc (k为大于零的整数)。
关于中国剩余定理的原理讲解可以参考这篇博客,非常清楚!膜大神orz中国剩余定理学习笔记
求解中国剩余定理时,一般会用到逆元。逆元的求法总结(3种基本方法+4种实现)
【接口】 int CRT(int a[],int m[],int n);复杂度 :O(nlogm),其中m和每个m i m_i m i 输入 :a,m——第i个方程表示为x ≡ a i ( m o d m i ) xequiv a_i(modspace m_i) x ≡ a i ( m o d m i ) spacespacespacespacespacespacespacespacespacespace 输出 :方程组在[ 0 , ∏ i = 0 n − 1 m i ) [0,prod_{i=0}^{n-1}m_i) [ 0 , ∏ i = 0 n − 1 m i ) 调用外部函数 :拓展欧几里得
【代码】
int CRT ( int a[ ] , int m[ ] , int n )
{
int M = 1 ;
for ( int i= 0 ; i< n; ++ i) M * = m[ i] ;
int ret = 0 ;
for ( int i= 0 ; i< n; ++ i)
{
int x, y;
int tm = M/ m[ i] ;
extend_gcd ( tm, m[ i] , x, y) ;
ret = ( ret+ tm* x* a[ i] ) % M;
}
return ( ret+ M) % M;
}
【接口】 int extend_gcd(int a,int b,int &x,int &y);复杂度 :O(logN),其中N和a,b同阶输入 :a,b——两个整数 spacespacespacespacespacespacespacespacespacespace 输出 :a和b的最大公约数
【代码】
int extend_gcd ( int a, int b, int & x, int & y )
{
if ( b== 0 )
{
x = 1 ;
y = 0 ;
return a;
}
else
{
int r = extend_gcd ( b, a% b, y, x) ;
y - = x* ( a/ b) ;
return r;
}
}