luogu P1038借教室【Noip提高组2012】

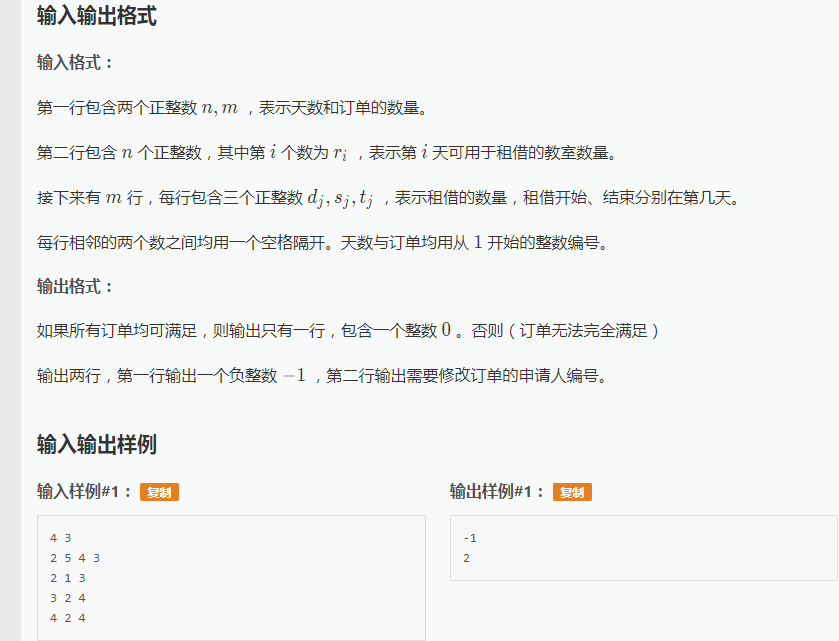
这道题我读完题目的第一感觉是：

这不就是个线段树？？用线段树维护区间最小值，检查是否满足订单要求即可判断。

对于修改操作直接在区间上进行。

据说会卡一卡线段树，但是貌似写一个懒标记，连zkw线段树都不用，然后读优，什么的随便卡卡就可以A了

后来想了想，就这么显然的直接拿线段树去A题显然没什么意义，于是决定想一波正解

正解的一般解法都是差分前缀和+二分

当然主要都是二分。

然后我绞尽脑汁不知道怎么写，后来发现是不会算复杂度限制了我的想象力。

二分天数十分显然，在1~m间二分，对于每一个mid,我们假定，订单就一定会在这一天出锅，然后剩下的就是判断这一天会不会出锅。

对于判断的方式，我们另开一个数组，记录类似订单能够为总的教室数量贡献或是拿走的信息

 我们假设这个数组是room_add，order_l, order_r, order_room分别代表订单从第order_l天开始到第order_r天结束，每天借order_room间教室

对于每份订单：在room_add[order_l[i]]上加上order_room, 相应的，在room_add[order_r[i]+1]上减去order_room

分别表示订单在order_l天得到了order_room间教室，而在order_r天失去了order_room间教室，也就是为下一个订单提供了order_room间教室。

我们很容易想到，对于两份相邻的订单，若是后一份订单得到的教室加上前一份订单失去的教室的数量比a[i]（a[i]表示每天能提供的教室数量）还大，说明我们肯定无法满足后一份订单，就出锅了。

但是我们二分的是在哪一天出锅，所以这个时候我们要把二分范围缩小

反之扩大

最后如果二分结束后r等于m，就表示中间一定有出过锅，导致r的范围缩小了

详细见代码实现

#include<bits/stdc++.h>
#define ll long long
#define uint unsigned int
using namespace std;
const int maxn = 1000086;
struct shiki {
    int l, r;
    int room;
}order[maxn];
int n, m;
int a[maxn], room_add[maxn];

inline int read() {
    int x = 0, y = 1;
    char ch = getchar();
    while(!isdigit(ch)) {
        if(ch == '-') y = -1;
        ch = getchar();
    }
    while(isdigit(ch)) {
        x = (x << 1) + (x << 3) + ch - '0';
        ch = getchar();
    }
    return x * y;
}

inline bool check(int aim_day) {
    memset(room_add, 0, sizeof(room_add));
    for(register uint i = 1; i <= aim_day; ++i) {
        room_add[order[i].l] += order[i].room;
        room_add[order[i].r + 1] -= order[i].room;
    }
    for(register uint i = 1; i <= n; ++i) {
        room_add[i] += room_add[i - 1];
        if(room_add[i] > a[i]) return true;
    }
    return false;
}

int main() {
    n = read(), m = read();
    for(int i = 1; i <= n; ++i)
         a[i] = read();
    for(int i = 1; i <= m; ++i)
        order[i].room = read(), order[i].l = read(), order[i].r = read();
    int l = 1, r = m;
    while(l < r) {
        int mid = l + r >> 1;
        if(check(mid)) r = mid;
        else l = mid + 1;
    }
    if(r != m) cout << -1 << '
' << l << '
';
    else cout << 0 << '
';
    return 0;
}