【XSY2741】网格 分治 LCT 并查集

题目描述

　　有一个(n imes m)的网格，线框的交点可以扭动，边不可伸缩。网格中有一些格子里面放了'x'形的支架，这些格子不会变形，但可以整体转动。如果所有格子都不能变形，那么称这个网格稳固。

　　有(q)个操作，每次改变一个格子的状态，即有支架给为无支架，无支架改为有支架。

　　请你判断初始及每次操作后这个网格是否稳固。

　　比如说下面这个网格就不稳固。

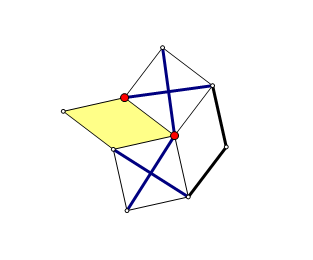
　　(n,mleq 3000,qleq 100000)

题解

　　先看看怎么判断一个网格是否稳固。

　　先给整个网格的左边和上边加上一行一列，然后把第一行的最左边两个格子设为有支架的格子，其他的设为没支架的格子。

　　样例那个图就会变成这样

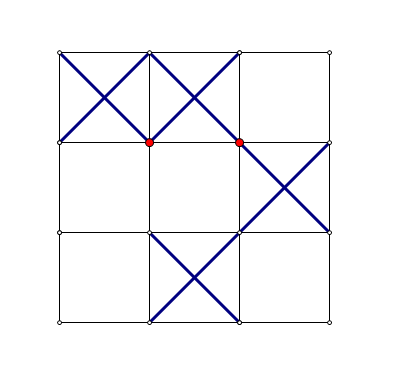
　　可以发现这样操作是不会改变整个图形的稳定性的。

　　设格子((i,j))右下角的角度为(a_{i,j}+90)。

　　因为一个交点四个角的度数和为(360)，所以可以列出以下方程：

[egin{align} 90+a_{i-1,j-1}+180-90-a_{i-1,j}+180-90-a_{i,j-1}+90+a_{i,j}&=360\ a_{i-1,j-1}+a_{i,j}-a_{i,j-1}-a_{i-1,j}&=0 end{align} ]

　　然后通过一些简单变换可以得到

[a_{0,0}+a_{i,j}-a_{0,j}-a_{i,0}=0 ]

　　因为(a_{0,0}=0)，所以方程简化为

[a_{i,j}=a_{i,0}+a_{0,j} ]

　　当((i,j))有支架时(a_{i,0}+a_{0,j}=a_{i,j}=0)，即(a_{i,0}=-a_{0,j})，那么我们就在图(G)的(i)和(j+n)两个点之间连一条边。

　　显然这个图是二分图。

　　因为边界上只有(a_{0,1}=0)，所以一个点只有和(n+1)号点((0,1))属于同一个联通块，这个点对应的角的角度才是确定的。

　　当((i,j))无支架时(a_{i.j}=a_{i,0}+a_{0,j})。如果(a_{i,0})和(a_{0,j})之间有一个没有确定，那么(a_{i,j})也没有确定。

　　所以说，这个网格是稳定的(Longleftrightarrow)图(G)只有一个联通块。

　　现在问题就变成了：有一个(n+m)个点的图，有(nm)条边，还有(q)个加边删边的操作。问操作前和每一次操作完后联通块个数是不是(1)。

　　用分治+并查集和LCT都可以做。

　　可以把一定存在的边先用路径压缩的并查集处理完。

　　分治+并查集：(O(nmalpha+qlog^2(n+m)))

　　LCT：(O(nmalpha+qlog (n+m)))

代码

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<utility>
#include<iostream>
#include<vector>
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
void open(const char *s)
{
#ifndef ONLINE_JUDGE
	char str[100];
	sprintf(str,"%s.in",s);
	freopen(str,"r",stdin);
	sprintf(str,"%s.out",s);
	freopen(str,"w",stdout);
#endif
}
vector<pii> a[400010];
int f[10010];
int r[10010];
int ans[100010];
int s1[10010];//x
int s2[10010];//f[x]
int s3[10010];//r[f[x]]
int top;
int n,m,q;
char s[10010];
int c[3010][3010];
int find(int x)
{
	return f[x]==x?x:find(f[x]);
}
int find2(int x)
{
	return f[x]==x?x:f[x]=find(f[x]);
}
int num=0;
int merge(int x,int y)
{
	x=find(x);
	y=find(y);
	if(x==y)
		return 0;
	if(r[x]>r[y])
		swap(x,y);
	top++;
	s1[top]=x;
	s2[top]=y;
	s3[top]=r[y];
	if(r[x]==r[y])
		r[y]++;
	f[x]=y;
	return 1;
}
int merge2(int x,int y)
{
	x=find(x);
	y=find(y);
	if(x==y)
		return 0;
	if(r[x]>r[y])
		swap(x,y);
	f[x]=y;
	if(r[x]==r[y])
		r[y]++;
	return 1;
}
void back()
{
	f[s1[top]]=s1[top];
	r[s2[top]]=s3[top];
	top--;
}
void add(int p,int l,int r,int x,int y,int L,int R)
{
	if(l<=L&&r>=R)
	{
		a[p].push_back(pii(x,y));
		return;
	}
	int mid=(L+R)>>1;
	if(l<=mid)
		add(p<<1,l,r,x,y,L,mid);
	if(r>mid)
		add((p<<1)|1,l,r,x,y,mid+1,R);
}
void solve(int l,int r,int p)
{
	int now=top;
	for(auto v:a[p])
		if(merge(v.first,v.second))
			num++;
	if(l==r)
		ans[l]=(num==n+m-1);
	else
	{
		int mid=(l+r)>>1;
		solve(l,mid,p<<1);
		solve(mid+1,r,(p<<1)|1);
	}
	while(top>now)
	{
		back();
		num--;
	}
}
int main()
{
	open("grid");
	scanf("%d%d%d",&n,&m,&q);
	memset(c,-1,sizeof c);
	for(int i=1;i<=n;i++)
	{
		scanf("%s",s+1);
		for(int j=1;j<=m;j++)
			if(s[j]=='x')
				c[i][j]=0;
	}
	for(int i=1;i<=n+m;i++)
	{
		f[i]=i;
		r[i]=1;
	}
	int x,y;
	for(int i=1;i<=q;i++)
	{
		scanf("%d%d",&x,&y);
		if(~c[x][y])
		{
			add(1,c[x][y],i-1,x,y+n,0,q);
			c[x][y]=-1;
		}
		else
			c[x][y]=i;
	}
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++)
			if(~c[i][j])
			{
				if(c[i][j])
					add(1,c[i][j],q,i,j+n,0,q);
				else
					if(merge2(i,j+n))
						num++;
			}
	for(int i=1;i<=n+m;i++)
		find2(i); 
	solve(0,q,1);
	for(int i=0;i<=q;i++)
		if(ans[i])
			printf("S
");
		else
			printf("U
");
	return 0;
}