我终于又厚颜无耻地赖着没走
......
T1 矩阵游戏
用了30hmin找规律,然后发现貌似具有交换律,然后发现貌似有通项公式,然后发现貌似每次操作对通项的影响是相同的,然后发现貌似跟N没啥关系...
确认过复杂度,是遇上了正解。
开心啊,码了1h,到八点半还过不去样例(skyh早做完了好像还过对拍了好像还高兴够呛),我都想弃了
突然过样例,看了看时间,只能放弃了给T1打对拍的习惯...
结束前半小时心态爆炸的时候给它补上了对拍放松心情233
T2 跳房子
考场上只打了NK模拟,虽然想出了循环节但是已经没信心去打了
传说中的分块思想被我打炸了,虽然后来颓到了贪心正确性的证明
但是还是用%%orz tkj线段树维护映射的做法做掉了
讲真那种做法真的挺优美的..
T3 优美序列
奇袭就不提了,当初颓的一批哪里还记得分治
于是新颓了一个题解..%%orz starsing
首先设一段区间内值域相邻的对数为num,则当l+num==r时,这是个优美区间
维护一个单调指针从左往右滑,每滑到一个新点,检查对num是否有贡献
然后用线段数维护r之前的点l到r这个区间的num(神奇,不知道怎么能想到)
其实为了方便,维护的是l+num,查询时直接与r比较,修改就是区间加
那么每移动一次r,可以知道可以更新哪些l了,可是还不知道应该何时更新
找到第一个可更新此区间的r时,就用小于待询区间l的最大l更新(其实只是赋值一次)待询区间的答案即可。
1.首先这个r是最小的r没问题吧,因为这是你第一次扫到
2.那你可能说了,将来会不会有更大的l出现,使得即使r也增大但是答案更优
3.偷starsing一张图: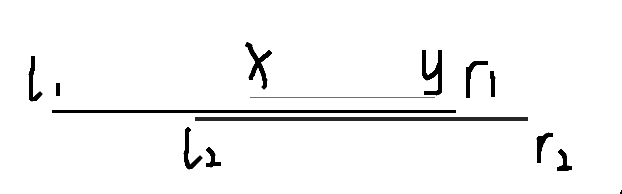
r1是你刚刚扫到的r,l1是刚刚用线段树找到的l,r2是你期望的r,l2是期望更大的l
所以[l1,r1],[l2,r2]都是优美区间...
妙的是,[l2,r1]也一定是优美区间。
不然呢,如果它不连续,那么它缺失的值域一定在左(右)边,右(左)边的区间就不可能优美了.
4.所以未来更优只是没经过分析yy出来的,还是尽快抓住现在取到最优解吧