如果用了>=3种颜色,这部分的方案数是x*(y+3)!%6=0,所以只考虑一种和两种
若m>0,则只能用两种,判断每个联通块是不是二分图,若不是则输出0
否则答案为$C_n^2(2^k-2)$
若m=0,再加上颜色数
设第i行的点数sx_i,列sy_i
对一个点(i,j)假如说sx_i>sy_j,那么说这个点是第j列的关键点,否则说它是第i行的关键点
那么一条线的关键点数量是不超过$sqrt{n}$级别的
那么考虑如何去完成这些操作
修改并维护最值
以一行为例,修改只暴力修改关键点(同时更新其所在列的答案),非关键点打上标记
查询一列时,暴力枚举关键点,带上其所在行打上的标记更新答案,而非关键点的答案是已经维护好的。
移动(合并)
那么其实需要完成的目标就是使得合并之后,查询每个点的标记是正确的,且仍然满足关键点的性质
维护标记:对于行列分别维护并查集,按秩合并,节点上维护标记差,每个位置的真实值就是父链求和
关键点:由于对于这两列来说,sy都增大了,所以只会出现原本的关键点变成非关键点的情况,暴力检查即可
去重
合并两列后原来两个横坐标相同的点就变成重点,那么关键点是$sqrt{n}$级别就不对了
所以要对关键点去重,为啥不对非关键点去重,感性理解的话大概因为它们本来就不会作为关键点被这一列暴
不影响这一列的复杂度而且也不影响其所在的行的复杂度(?),所以先放着不管
每次合并都去重的话就是hash,然后也可以达到一定数目比如$1.5sqrt{n}$就暴扫重构
每次一定删除$sqrt{n}$级别的点,所以复杂度$nsqrt{n}logn$?我并没把这题A掉所以可能胡了
T3 好像已经讲过?
首先冷静一点发现答案就是枚举所有xor和为0的集合S然后累加2^|S|
部分分1 值域小
dp[i][j]表示前i个点xor和为j的答案和
$dp[i-1][j]->dp[i][j]$,$dp[i-j][j^a[i]]->dp[i][j]$
部分分2 种类少
每种数选奇数或偶数个的效果相同,预处理每种数选何种奇偶性的方案数(大概是一些组合数相加)
然后还用上边那种dp
部分分3 $bit3^{bit}$可过
发现dp转移的过程其实是对$[1,0,0......0,2,0......0]$做xor卷积,最后得到的结果的第0位就是答案
怎么球呢,由于这个数组特别特别稀疏,可以发现在fwt后每个位置上只有2种值$1+2$和$1-2$
$max_{a}*n+max_{a}log$?
其实只需要知道里边有几个-1
什么时候第i个数组的第x位是-1,当$bitcnt(a_i and x)$是奇数时
考虑枚举$t=bitcnt(a_i and x)$,再枚举$s$是t的超集,s的权值是$a_i=s$的i的个数
什么样的x会得到s的权值个数量的-1,即除了t以外的部分s和x无交
那么s的贡献是针对一个子集,感觉上大概可以这样做:
s的贡献送给$U^s$,然后超集求和,设每个位置的值为$v_i$
对于一个x,枚举其所有大小为奇数的子集y,累加$v_{x^y}$即为-1的个数
部分分4 $bit2^{bit}$可过
FWT的和等于和的FWT
所以先求和,再FWT,可以知道若干-1和若干3的和是多少
又知道总共是n个,可以解出个数
或者想到要求和但是没想到FWT的和等于和的FWT
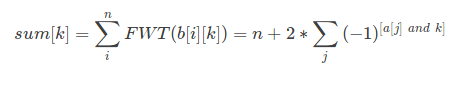
$sumlimits_j (-1)^{|a[j] and k|}$还是FWT