LeetCode: Linked List Cycle I && II

I 

title:

Given a linked list, determine if it has a cycle in it.

Follow up:
Can you solve it without using extra space?

思路：

使用两个指针slow,fast。两个指针都从表头开始走，slow每次走一步，fast每次走两步，如果fast遇到null，则说明没有环，返回false；如果slow==fast，说明有环，并且此时fast超了slow一圈，返回true。

为什么有环的情况下二者一定会相遇呢？因为fast先进入环，在slow进入之后，如果把slow看作在前面，fast在后面每次循环都向slow靠近1，所以一定会相遇，而不会出现fast直接跳过slow的情况。

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    bool hasCycle(ListNode *head) {
        ListNode* fast = head;
        ListNode* slow = head;
        while (fast && fast->next){
            slow = slow->next;
            fast = fast->next->next;
            if (slow == fast){
                break;
            }
        }
        return !(fast == NULL || fast->next == NULL);
    }
};

II

title：

Given a linked list, return the node where the cycle begins. If there is no cycle, return null.

Follow up:
Can you solve it without using extra space?

思路：

首先我们看下面这张图：

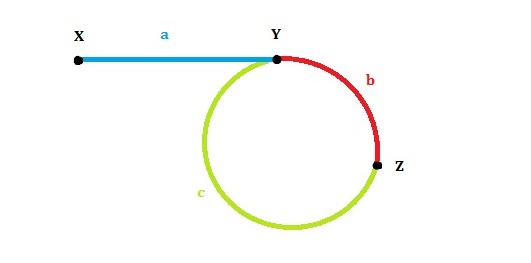
设：链表头是X，环的第一个节点是Y，slow和fast第一次的交点是Z。各段的长度分别是a,b,c，如图所示。环的长度是L。slow和fast的速度分别是qs,qf。

 假设圈的周长L

那么相遇的时候slow走：a + b,而fast走：a + b + n*L，（n代表fast走了多少圈）

fast走路的路程是slow的两倍，那么2(a+b) = a + b + n*L，得到a = n*L - b

从相遇点的时候开始，放一个指针从开始点走起，另一个指针继续走，而且这时走的速度都是一样的，那么当一个指针从开始点X走到循环圈点Y的时候，走了a路程，而另一个指针走的路程是n*L-b，那么两者的路程是一样的，相遇点必然是Y。

从而定理得到证明，而不管这个圈的大小。

这样的证明够严密了，哪里用得着那么啰嗦，什么圈大圈小的都可以不用管。圈大的时候，不过是n == 1的特殊情况。

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        ListNode*fast = head;
        ListNode*slow = head;
        while (fast && fast->next){
            slow = slow->next;
            fast = fast->next->next;
            if (slow == fast)
                break;
        }
        if (!fast|| !fast->next)
            return NULL;
        slow = head;
        while (slow != fast){
            slow = slow->next;
            fast = fast->next;
        }
        return slow;
    }
};

扩展问题

在网上搜集了一下这个问题相关的一些问题，思路开阔了不少，总结如下：

1. 环的长度是多少？

2. 如何将有环的链表变成单链表（解除环）？

（1）第一次相遇后，让slow,fast继续走，记录到下次相遇时循环了几次。因为当fast第二次到达Z点时，fast走了一圈，slow走了半圈，而当fast第三次到达Z点时，fast走了两圈，slow走了一圈，正好还在Z点相遇。

（2）在II中的Y处断开即可