为什么要使用二叉树?
二叉树结合了有序数组(假设数组中所有数据项都有序的排列,用二分查找法可以在有序数组中快速地找到特定的值)和链表(链表的插入和删除操作很快)这两种数据结构。在树中查找数据项的速度和有序数组查找一样快,并且插入数据项和删除数据项的速度也和链一样快。
二叉树解决了在有序数据中插入数据项太慢(有序数组插入、删除数据时要移动很多次数组元素的位置,平均要移动数组中的一半数据项,即N/2次移动)的问题;
同时也解决了在链表中查找太慢(链表中查找必须从头开始,依次访问链表中的每一个数据项,直到找到该数据项为止,因此平均需要访问N/2个数据项)的问题。
1、树
树由边连接的节点而构成。下图就显示了一棵树。图中的圆代表节点,连线圆的直线代表边。
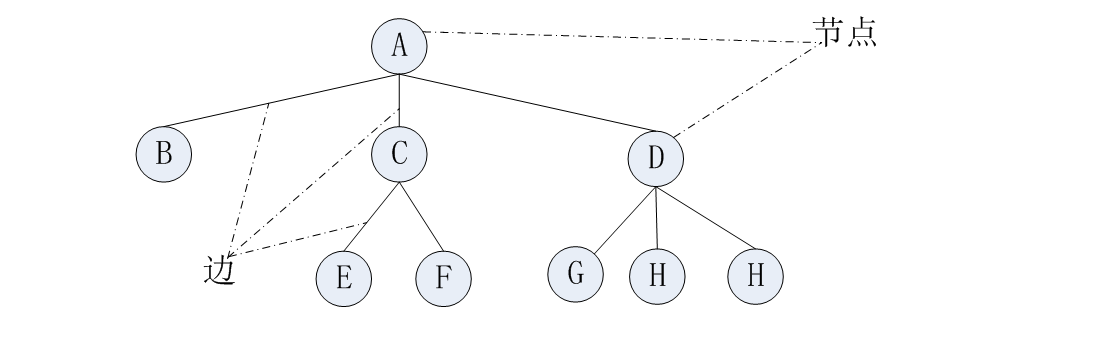
【图1】
节点间的直线(边)表示关联节点间的路径。在树的顶层总是只有一个节点,它通过边连接到第二层的多个节点,然后第二层节点连向第三层更多的节点,依次类推。所以树的顶部小,底部大。也就像树倒过来了一样。这样的从顶到底来思考问题更自然。不过本篇文章只讨论一种特殊的树------二叉树。二叉树的每个节点最多有两个子节点。更普通的数据里,节点的子节点可以多于两个,这种树称为多路数。
树的术语
路径:设想一下顺着连接节点的边从一个节点走到另外一个节点,所经过的节点的顺序排序就称为“路劲”。
根:树顶端的节点称为“根”。一棵树只有一个根。如果要把一个节点和边的集合定义为树,那么从根到其他任何一个节点必须有一条(而且只有一条)路径。图2展示的就不是树。
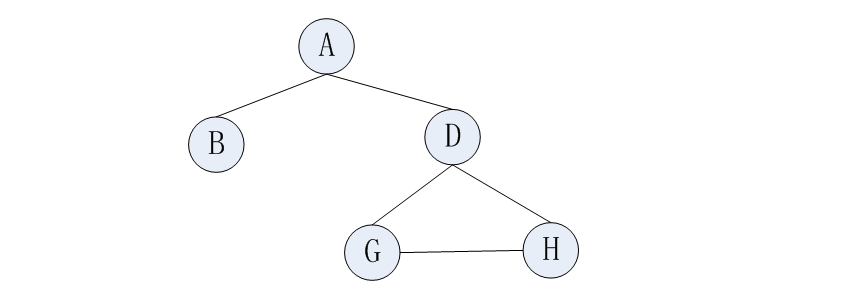
【图2】
父节点:每个节点(除了根)都恰好有一条边向上连接到另一个节点,上面的这个节点就称为下面节点的“父节点”。
子节点:每个节点都可能有一条或多条边向下连接其他节点,下面的这些节点就称为它的“子节点”。
叶节点:没有子节点的节点称为“叶子结点”或简称“叶节点”。树中只有一个根,但可以有很多个叶节点。
子树:每个节点都可以称为“子树”的根。它和它所有的子节点,子节点的子节点等都还含在子树中,就像家族中那样,一个节点的子树包含它所有的子孙。
访问:当程序控制流程到达某个节点时,就称为“访问”这个节点,通常是为了在这个节点处执行某种程序,例如查看节点某个数据字段的值或显示节点。
遍历:遍历树意味着要遵循某种特定的顺序访问书中所有节点。例如,可以按关键字值的升序访问所有的节点。
层:一个节点的层数是指从根开始到这个节点有多少“代”。例如,可以按关键字的升序访问所有的节点。当然还有其他的顺序来遍历一棵树。
关键字:可以看到,对象中通常会有一个数据域被指定为关键字值。
深度:对于任意节点n,n的深度为从根到n的唯一路径长,根的深度为0。
高度:对于任意节点n,n的高度为从n到一片树叶的最长路径长,所以树叶的高度为0。
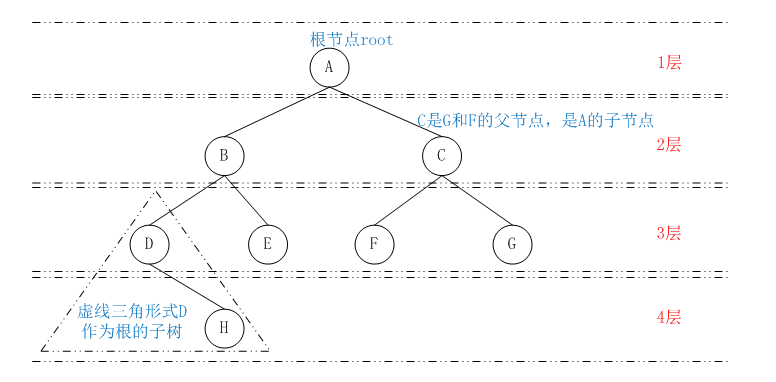
【图3】
2、二叉树
如果树中每个节点最多只能有两个子节点,这样的树就称为“二叉树”。二叉树简单,而且最常用。
二叉树每个节点的两个子节点称为“左子节点”和“右子节点”,分别对应树图形中的他们的位置。二叉树中的节点不是必须有两个子节点:它可以只有一个左子节点,或者只有一个右子节点,或者没有子节点(这样的情况下它就是叶节点)。
注意:二叉搜索树(binary search tree)特征的定义可以这样说:一个节点的左子节点的关键字值小于这个节点,右子节点的关键字值大于或等于这个父节点。如图4
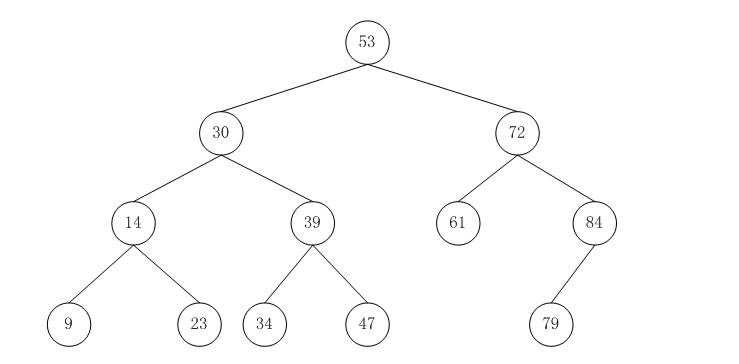
【图4】
在搜索二叉树(Bianry Tree)中怎么查找一个节点,怎么插入新节点,怎么遍历树,以及怎么删除节点。下面将会详细介绍。
二叉树的节点类定义:
public class Node<T extends Comparable<T>> { // 左子节点 protected Node<T> leftChild; // 右子节点 protected Node<T> rightChild; // 节点数据 protected T data; /** * 打印节点内容 */ public void print() { System.out.println(data); } }
二叉树类定义:
public interface Tree<T extends Comparable<T>> { /** * 返回root * */ public Node<T> getRoot(); /** * 查找节点 * */ public Node<T> find(T data); /** * 插入节点 * */ public boolean insert(Node<T> node); /** * 删除节点 * */ public boolean delete(T data); /** * 中序遍历 * */ public void infixOrder(Node<T> node); /** * 前序遍历 * */ public void preOrder(Node<T> node); /** * 后序遍历 * */ public void postOrder(Node<T> node); /** * 查找最大 * */ public Node<T> findMax(); /** * 查找最小 * */ public Node<T> findMin(); }
备注:以下将以搜索二叉树的查找节点、插入节点、遍历树、查找最大值和最小值、删除节点。
3、查找节点
/** * 根据指定的节点字值 */ public Node<T> find(T data) { // 从root节点开始查找 Node<T> current = getRoot(); // 对比,一直对比到节点为null或者找到节点值与指定的节点值相同为止。 while (current.data != data) { // 如果查找的节点值比当前节点值小,则下次对比当前节点的左子树节点 if (data.compareTo(current.data) < 0) { current = current.leftChild; } // 如果查找的节点值比当前节点值大,则下次对比当前节点的右子树节点 else { current = current.rightChild; } // 如果对比节点为null,则直接返回null,代表没有找到 if (current == null) { return null; } } return current; }
这个方法中变量current是保存正在查看的节点,参数data是找到节点的值。查找从根开始(在树中只能这么做,因为只有跟节点可以直接访问)。因此,开始把current设置根、
之后,在while循环中,将要查找的节点值data与当前的节点值作对比。如果key小于这个当前节点值,current赋值为此节点的左子节点;如果data大于或等于当前节点值,current赋值为当前节点的右子节点。
找不到节点:如果current等于null,在查找的搜索二叉树中找不到下一个子节点:到达序列的末端而没有找到要找的节点,表名了不存在,返回null。
找到节点:如果找到,则返回找到的节点。
查找的时间复杂度是:查找节点的时间取决于这个节点所在的层数,每一层最多有2n-1个节点,总共N层共有2n-1个节点。O(log N),更详细的说是O(log2N),以2为底的对数,N是树的层数。如果一个层为5的搜索二叉树中,根据节点值查找节点,那么做到只需要5次比较,就可以查找完成。
4、插入节点
要插入节点,必须先找到插入的地方。这个很像要找到一个不存在的节点的过程,如前面说的找不到节点的情况下。从根开始查找一个想的节点,它将是这个新节点的父节点。但父节点找到了,新的节点就可以连接到它的左子树或右子树节点处,这取决于新节点的值时比父节点的值大还是小。
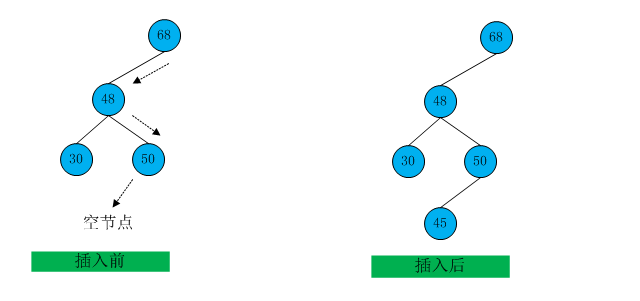
如图5中插入前,此时要插入的节点时45时,图5展示了插入45的流程。
【图5】
45比60小,但是比48大,所以转到节点50,。然后45小于50,因此要向50的左子节点转,但是50没有左子节点,因此插入的新节点的位置就是50的左子节点。
/** * 插入新的节点 */ public boolean insert(Node<T> node) { Node<T> newNode = new Node<T>(); newNode.data = node.data; if (getRoot() == null) { // 如果root节点null,则插入的节点位置就是root节点位置 root = newNode; return true; } else { // 如果root节点不为null,则从root节点开始查找要插入的位置 Node<T> current = root; // 从root节点开始查找要插入的位置 Node<T> parent; while (current != null) { parent = current; if (newNode.data.compareTo(current.data) < 0) { // 如果待插入节点值小于当前节点的值,则向当前节点左子节点查找 current = current.leftChild; if (current == null) { // 如果当前节点的左子节点为null,则插入的节点位置就是当前节点的左子节点,否则,继续循环查找。 parent.leftChild = newNode; return true; // 返回插入状态 } } else { // 否则(待插入节点值大于或等于当前节点值),向当前节点的右子节点查找(假设,插入节点值在当前树中不存在) current = current.rightChild; if (current == null) { // 如果当前节点的右子节点为null,则插入的节点位置就是当前节点的左子节点,否则,继续循环查找。 parent.rightChild = newNode; return true; // 返回插入状态 } } } return false; } }
5、遍历树
遍历树的意思是根据一种特定的顺序访问树中的每一个节点。这个过程不如查找、插入和删除节点常用,其中一个原因是因为遍历的速度不是特别块。不过遍历树在某些情况下是有用的,而且在理论上很有意义。
有三种简单的方法遍历树:前序(preorder)、中序(inorder)、后序(postorder)。二叉搜索树常用的遍历方式中最常用的遍历方式是中序遍历。
5.1、中序遍历(inorder):
中序遍历二叉搜索树会使所有的节点关键字值升序被访问到。如果希望在二叉树中创建有序的数据序列,这是一种方法。遍历树最简单的方法就是用递归的方法,用递归的方法遍历整棵树要用一个节点作为参数。初始化时这个几点就是根。这个方法只需要做三件事:
1)调用自身遍历节点的左子树;
2)访问这个节点;
3)调用自身遍历节点的右子树。
遍历可以应用于任何二叉树,而不只是二叉搜索树。这个遍历的原理不关心节点的关键字值:它只是看这个几点是否有子节点。
/** * 中序遍历 * */ public void infixOrder(Node<T> node) { if(node!=null){ infixOrder(node.leftChild); //1)调用自身遍历节点的左子树; System.out.println(node.data); //2)访问这个节点; infixOrder(node.rightChild); //3)调用自身遍历节点的右子树。 } }
开始是用根作为参数调用这个防范:
infixOrder(root);
之后,它就靠自己递归调用自己,直到所有节点都被访问过为止。
5.2、前序遍历(preorder):
1)访问这个节点;
2)调用自身遍历节点的左子树;
3)调用自身遍历节点的右子树。
/** * 前序遍历 * */ public void preOrder(Node<T> node) { if(node!=null){ infixOrder(node.leftChild); //1)访问这个节点; System.out.println(node.data); //2)调用自身遍历节点的左子树; infixOrder(node.rightChild); //3)调用自身遍历节点的右子树。 } }
5.3、后序遍历(postorder):
1)调用自身遍历节点的左子树;
2)调用自身遍历节点的右子树;
3)访问这个节点。
/** * 后序遍历 * */ public void postOrder(Node<T> node) { if(node!=null){ infixOrder(node.leftChild); //1)调用自身遍历节点的左子树; System.out.println(node.data); //2)调用自身遍历节点的右子树; infixOrder(node.rightChild); //3)访问这个节点。 } }
6、查找最大值和最小值
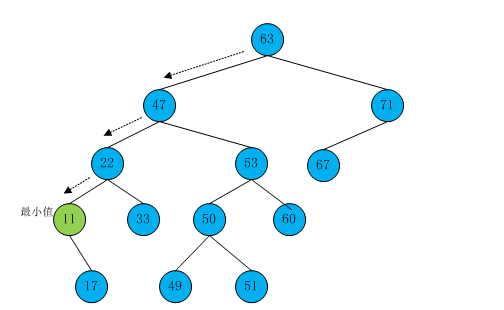
在二叉搜索树中得到最大值和最小值比较容易。要找最小值时,先找到根的左子树节点处,然后接着走到那个子节点的左子节点,如此类推,直到找到一个没有左子树的节点,这个节点就是最小值的节点。
【图6】
下面就是找到最小关键字值的节点的方法代码:
/** * 找到最小值 * */ public Node<T> findMin() { Node<T> current=null; Node<T> last=null; current=root; while (current!=null) { last=current; current=current.leftChild; } return last; }
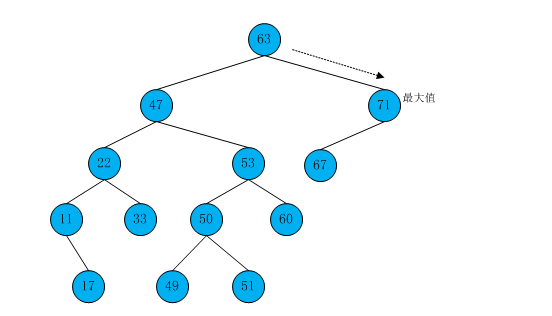
按照相同的步骤来查找树中的最大值,不过要找到右子节点,一直向右找到没有右子树的节点,这个节点就是最大值的节点。
【图7】
/** * 找到最大值 * */ public Node<T> findMax() { Node<T> current=null; Node<T> last=null; current=root; while (current!=null) { last=current; current=current.rightChild; } return last; }
7、删除节点
删除节点是二叉搜索树常用的一般操作中最复杂的,但是,删除节点在很多树的应用中又非常重要,所以要详细研究总结特点。
删除节点要从查找要删除的节点开始入手,方法与前面介绍的find().和insert()相同。找到节点后,这个要删除的节点可能会有三种情况需要考虑:
- 该节点是叶子结点(没有子节点)。
- 该节点有一个子节点。
- 该节点有两个子节点。
下面将依次讲解这三种情况。第一种最简单;第二种比较单间;第三种就相当于复杂了。
7.1、删除没有子节点的节点
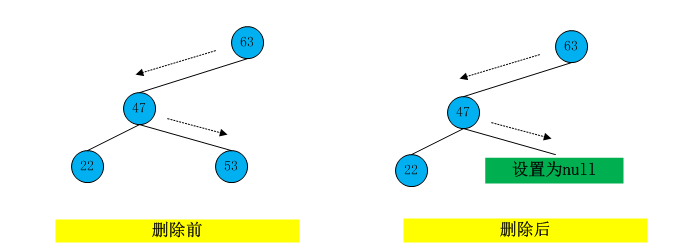
要删除叶节点,只需要该节点的父节点的对应的子节点为null就可以。
【图7】
delete()方法的第一步和find()、insert()方法很像。它查找待删除的节点。和insert()方法一样,需要保存要删除节点的父节点,这样就可以修改它的子字段值。如果找到了,就从while循环中跳出,parent保存要删除的节点,如果找不到要删除的节点,就从delete()方法返回false。
/** * 删除节点 * */ public boolean delete(T data) { Node<T> current=root; Node<T> parent=root; boolean isLeftChild=true; while (current.data!=data) { //搜索待刪除节点 parent=current; if(data.compareTo(current.data)<0){ //如果待删除节点值比当前节点的值小,则向左节点查找。 isLeftChild=true; current=current.leftChild; }else{ //否则(小于,等于时就会跳出while了),向右节点查找。 isLeftChild=false; current=current.rightChild; } if(current==null){ //如果带查找节点为null,则返回,代表没有查找到待删除节点。 return false; } } // 1) 该节点(待删除节点)是叶子结点(没有子节点)。 if(current.leftChild==null&¤t.rightChild==null){ } // 2) 该节点(待删除节点)有一个子节点。 else if(current.leftChild==null){ }else if(current.rightChild==null){ } // 3) 该节点(待删除节点)有两个子节点。 else{ } return false; }
找到节点后,先要检查它是不是真的没有子节点。如果它没有子节点,还需要检查它是不是根。如果它是根节点的话,只需要把它置为null;这样就清空了整棵树。否则,就把父节点的leftChild或者rightChild置为null,断开父节点和那个要删除的节点的连接。并返回true(代表删除成功)。
// 1) 该节点(待删除节点)是叶子结点(没有子节点)。 if(current.leftChild==null&¤t.rightChild==null){ if(current==root) root=null; else if(isLeftChild) parent.leftChild=null; else parent.rightChild=null; return true; }
7.2、删除有一个子节点的节点
这个待删除节点只有两个连接:连向父节点的和连向它唯一的子节点的。需要从这序列中“剪断”这个节点,把的子节点直接连到它的父节点上。这个过程要求改变父节点适当的引用(左子节点或右子节点),指向要删除节点的子节点。
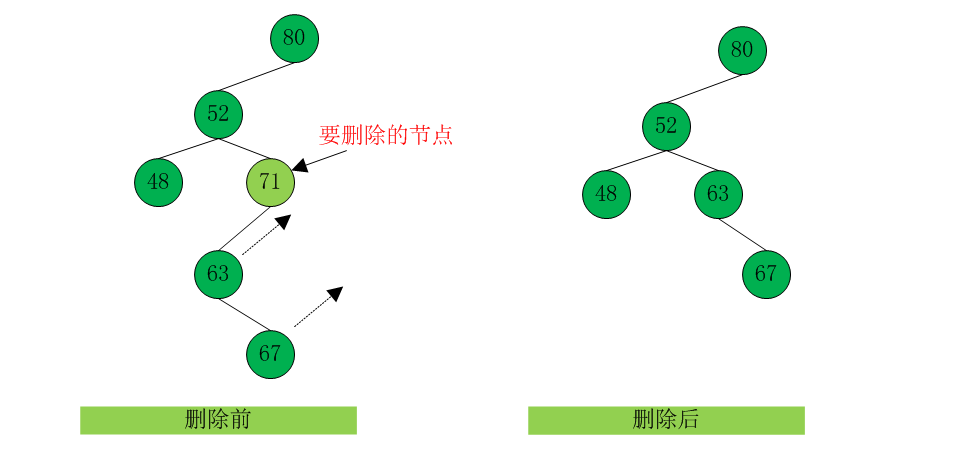
【图8】
在删除71节点后,它的位置被它的左子节点63取代了。实际上,63作为根的整棵树上移,作为52的新的右子节点插入。
如果待删除节点的右子节点为null
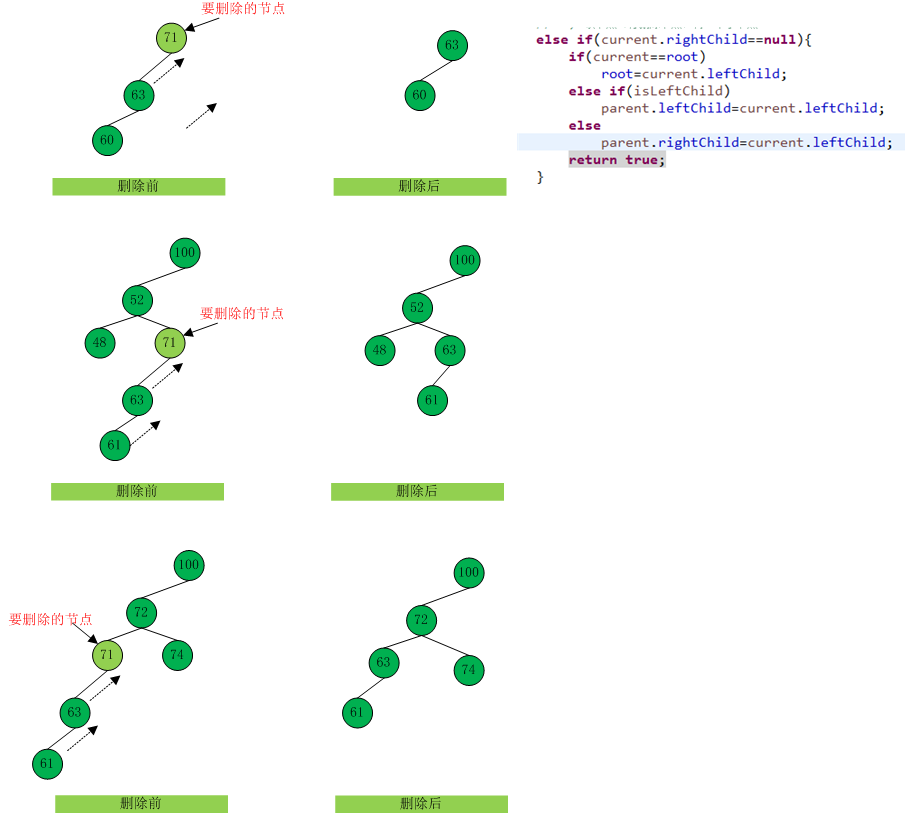
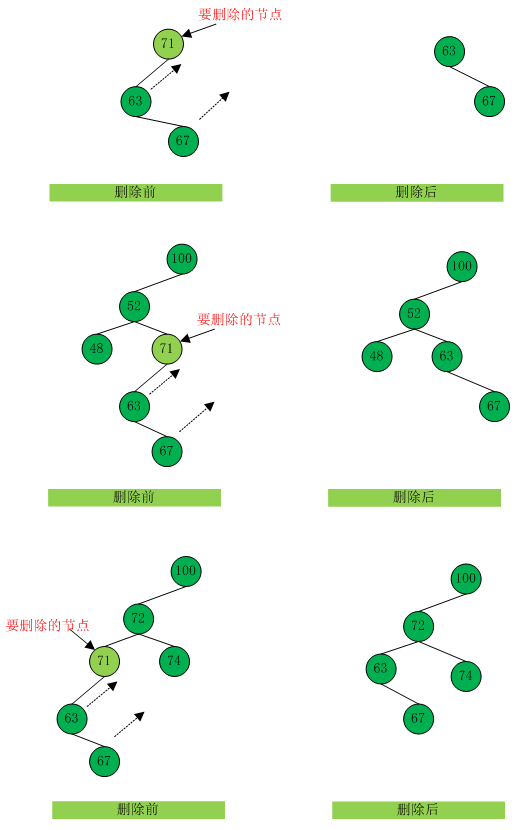
【图9】
如果左子节点为null,也同理。
全部代码:
// 2) 该节点(待删除节点)有一个子节点。 else if(current.rightChild==null){ if(current==root) root=current.leftChild; else if(isLeftChild) parent.leftChild=current.leftChild; else parent.rightChild=current.leftChild; return true; } else if(current.leftChild==null){ if(current==root) root=current.rightChild; else if(isLeftChild) parent.leftChild=current.rightChild; else parent.rightChild=current.rightChild; return true; }
7.3、删除有两个子节点的节点
如果要删除的节点有两个子节点,就不能只是用它的一个子节点代替它,为什么不能这样呢?

【图10】
如上图,假设要删除节点25,并且用它的右子树的根35取代它,那么35的左子树应该是谁呢?是删除节点25的左子节点15,还是35原来的左子节点30?然而在这两种情况中30都会放的位置不对,但又不能删除它。
因此就需要其他方法,二叉搜索树中的节点是按照升序的关键字值排序的。对每一个节点来说,比该节点的关键字值次高的节点是它的中序后继,可以简称为该节点的后继。在【图11】中,节点30就是25的后继。

【图11】
那么删除有两个子节点的节点,用它的中序后继来替代该节点,【图11】显示的就是要删除节点用它的后继代替它的情况。注意现在节点还是有序的。(这里还有更复杂的情况,就是当他的后继自己也有了子节点,后面会讨论这种可能性。)
找后继节点
首先,程序找到初始化节点的右子节点,它的关键字值一定比初始化节点大。然后转到初始节点的右子节点的左子节点那里(如果有的话),然后到这个左子节点的左子节点,以此类推,顺着左子节点的路径一直向下找。这个路径上最后一个左子节点就是初始化节点的后继。如【图12】
为什么可以用这个算法?这里实际上是要找比初始化节点关键字值大的节点集合中的最小的一个节点。当找到初始化节点的右子节点是,这个以右子节点为根的子树的所有节点都比初始节点的关键字值大,因为这是二叉搜索树所定义的。现在要找到这棵子树中值最下的节点。找子树的最小值,就应该顺着所有左子树节点的路径找下去。因此,这个算法可以找到比初始化节点大的最小的节点:它就是要找的后继。
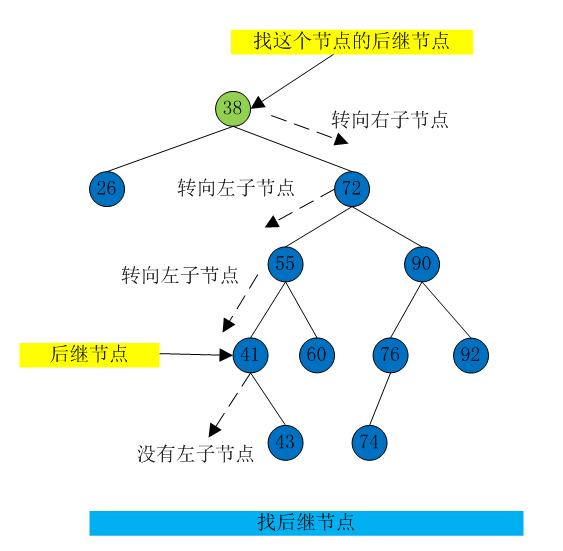
【图12】
如果初始节点的右子节点没有左子节点,那么这个右子节点本身就是后继。如【图13】
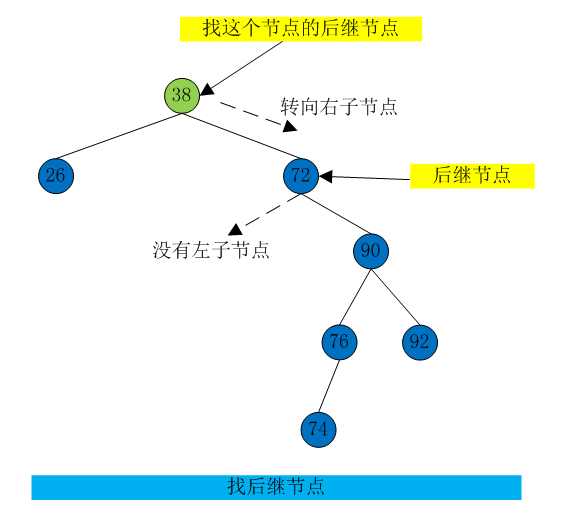
找后继节点的Java代码
/** * 找后继节点(Find Successor Node). * * @param delNode * 要刪除的节点 */ private Node<T> findSuccessorNode(Node<T> delNode) { Node<T> successorParent = delNode; Node<T> successor = delNode; Node<T> current = delNode.rightChild; // 向待删除节点的右子节点查找 while (current != null) { // 向待删除节点的右子节点的左子节点。。。依次循环查找直到左子节点没有左子节点为止。 successorParent = successor; successor = current; current = current.leftChild; } // 如果“后继节点”不是“待删除节点的右子节点”的话,需要维护“后继节点”的右子树(其无左子树),把后继节点的右子树转义给“后继节点的父节点“作为“后继节点的父节点“的左子节点、 if (successor != delNode.rightChild) { successorParent.leftChild = successor.rightChild; } return successor; }
删除业务代码
// 3) 该节点(待删除节点)有两个子节点。 else { // 查找“后继节点” Node<T> successor = findSuccessorNode(current); if (current == root) { root = successor; } else if (isLeftChild) { // 如果"待删除节点"是其父节点的左子节点,则直接将“后继节点”设置为“待删除节点的左子树”,并且设置“后继节点”的左子树为“待删除节点的左子树”。 parent.leftChild = successor; } else { // 如果“待删除节点”是其父节点的右子节点,则直接将“后继节点”设置为“待删除节点的右子树”,并且设置“后继节点”的左子树为“待删除节点的左子树”。 parent.rightChild = successor; } // 把待删除节点的左子树作为后继节点的左子树 successor.leftChild = current.leftChild; // 把待删除节点的右子树作为后继节点的右子树 successor.rightChild = current.rightChild; return true; }
整个二叉搜索树的全部代码如下:
Node.java
package com.dx.learning.binarytree; public class Node<T extends Comparable<T>> { // 左子节点 protected Node<T> leftChild; // 右子节点 protected Node<T> rightChild; // 节点数据 protected T data; /** * 打印节点内容 */ public void print() { System.out.println(data); } }
Tree.java(二叉树接口定义)
package com.dx.learning.binarytree; public interface Tree<T extends Comparable<T>> { /** * 返回root * */ public Node<T> getRoot(); /** * 查找节点 * */ public Node<T> find(T data); /** * 插入节点 * */ public boolean insert(Node<T> node); /** * 删除节点 * */ public boolean delete(T data); /** * 中序遍历 * */ public void infixOrder(Node<T> node); /** * 前序遍历 * */ public void preOrder(Node<T> node); /** * 后序遍历 * */ public void postOrder(Node<T> node); /** * 查找最大 * */ public Node<T> findMax(); /** * 查找最小 * */ public Node<T> findMin(); /** * 打印节点 * */ public void print(); }
BinaryTree.java(二叉搜索树定义)
package com.dx.learning.binarytree; import java.util.ArrayList; import java.util.List; public class BinaryTree<T extends Comparable<T>> implements Tree<T> { private Node<T> root; /** * 返回root */ public Node<T> getRoot() { return root; } /** * 根据指定的节点字值 */ public Node<T> find(T data) { // 从root节点开始查找 Node<T> current = getRoot(); // 对比,一直对比到节点为null或者找到节点值与指定的节点值相同为止。 while (current.data != data) { // 如果查找的节点值比当前节点值小,则下次对比当前节点的左子树节点 if (data.compareTo(current.data) < 0) { current = current.leftChild; } // 如果查找的节点值比当前节点值大,则下次对比当前节点的右子树节点 else { current = current.rightChild; } // 如果对比节点为null,则直接返回null,代表没有找到 if (current == null) { return null; } } return current; } /** * 插入新的节点 */ public boolean insert(Node<T> node) { Node<T> newNode = new Node<T>(); newNode.data = node.data; if (getRoot() == null) { // 如果root节点null,则插入的节点位置就是root节点位置 root = newNode; return true; } else { // 如果root节点不为null,则从root节点开始查找要插入的位置 Node<T> current = root; // 从root节点开始查找要插入的位置 Node<T> parent; while (current != null) { parent = current; if (newNode.data.compareTo(current.data) < 0) { // 如果待插入节点值小于当前节点的值,则向当前节点左子节点查找 current = current.leftChild; if (current == null) { // 如果当前节点的左子节点为null,则插入的节点位置就是当前节点的左子节点,否则,继续循环查找。 parent.leftChild = newNode; return true; // 返回插入状态 } } else { // 否则(待插入节点值大于或等于当前节点值),向当前节点的右子节点查找(假设,插入节点值在当前树中不存在) current = current.rightChild; if (current == null) { // 如果当前节点的右子节点为null,则插入的节点位置就是当前节点的左子节点,否则,继续循环查找。 parent.rightChild = newNode; return true; // 返回插入状态 } } } return false; } } /** * 删除节点 */ public boolean delete(T data) { Node<T> current = root; Node<T> parent = root; boolean isLeftChild = true; while (current.data != data) { // 搜索待刪除节点 parent = current; if (data.compareTo(current.data) < 0) { // 如果待删除节点值比当前节点的值小,则向左节点查找。 isLeftChild = true; current = current.leftChild; } else { // 否则(小于,等于时就会跳出while了),向右节点查找。 isLeftChild = false; current = current.rightChild; } if (current == null) { // 如果带查找节点为null,则返回,代表没有查找到待删除节点。 return false; } } // 1) 该节点(待删除节点)是叶子结点(没有子节点)。 if (current.leftChild == null && current.rightChild == null) { if (current == root) root = null; else if (isLeftChild) parent.leftChild = null; else parent.rightChild = null; return true; } // 2) 该节点(待删除节点)有一个子节点。 else if (current.rightChild == null) { if (current == root) root = current.leftChild; else if (isLeftChild) parent.leftChild = current.leftChild; else parent.rightChild = current.leftChild; return true; } else if (current.leftChild == null) { if (current == root) root = current.rightChild; else if (isLeftChild) parent.leftChild = current.rightChild; else parent.rightChild = current.rightChild; return true; } // 3) 该节点(待删除节点)有两个子节点。 else { // 查找“后继节点” Node<T> successor = findSuccessorNode(current); if (current == root) { root = successor; } else if (isLeftChild) { // 如果"待删除节点"是其父节点的左子节点,则直接将“后继节点”设置为“待删除节点的左子树”,并且设置“后继节点”的左子树为“待删除节点的左子树”。 parent.leftChild = successor; } else { // 如果“待删除节点”是其父节点的右子节点,则直接将“后继节点”设置为“待删除节点的右子树”,并且设置“后继节点”的左子树为“待删除节点的左子树”。 parent.rightChild = successor; } // 把待删除节点的左子树作为后继节点的左子树 successor.leftChild = current.leftChild; // 把待删除节点的右子树作为后继节点的右子树 successor.rightChild = current.rightChild; return true; } } /** * 找后继节点(Find Successor Node). * * @param delNode * 要刪除的节点 */ private Node<T> findSuccessorNode(Node<T> delNode) { Node<T> successorParent = delNode; Node<T> successor = delNode; Node<T> current = delNode.rightChild; // 向待删除节点的右子节点查找 while (current != null) { // 向待删除节点的右子节点的左子节点。。。依次循环查找直到左子节点没有左子节点为止。 successorParent = successor; successor = current; current = current.leftChild; } // 如果“后继节点”不是“待删除节点的右子节点”的话,需要维护“后继节点”的父节点,把后继节点的右子树转义给“后继节点的父节点“作为“后继节点的父节点“的左子节点、 if (successor != delNode.rightChild) { successorParent.leftChild = successor.rightChild; } return successor; } /** * 中序遍历 */ public void infixOrder(Node<T> node) { if (node != null) { infixOrder(node.leftChild); // 1)调用自身遍历节点的左子树; System.out.println(node.data); // 2)访问这个节点; infixOrder(node.rightChild); // 3)调用自身遍历节点的右子树。 } } /** * 前序遍历 */ public void preOrder(Node<T> node) { if (node != null) { infixOrder(node.leftChild); // 1)访问这个节点; System.out.println(node.data); // 2)调用自身遍历节点的左子树; infixOrder(node.rightChild); // 3)调用自身遍历节点的右子树。 } } /** * 后序遍历 */ public void postOrder(Node<T> node) { if (node != null) { infixOrder(node.leftChild); // 1)调用自身遍历节点的左子树; System.out.println(node.data); // 2)调用自身遍历节点的右子树; infixOrder(node.rightChild); // 3)访问这个节点。 } } /** * 找到最大值 */ public Node<T> findMax() { Node<T> current = null; Node<T> last = null; current = root; while (current != null) { last = current; current = current.rightChild; } return last; } /** * 找到最小值 */ public Node<T> findMin() { Node<T> current = null; Node<T> last = null; current = root; while (current != null) { last = current; current = current.leftChild; } return last; } /** * 打印节点 * */ public void print() { StringBuilder builder = new StringBuilder(); List<Node<T>> parentNodes = new ArrayList<Node<T>>(); List<Node<T>> childNodes = new ArrayList<Node<T>>(); parentNodes.add(root); System.out.println("--------------------------------------------------------------------------------"); System.out.println("root:" + root.data); for (int i = 0; i < parentNodes.size(); i++) { Node<T> currentNode = parentNodes.get(i); if (currentNode.leftChild != null) { builder.append(currentNode.data + "<-" + currentNode.leftChild.data); childNodes.add(currentNode.leftChild); } else { builder.append(currentNode.data + "->" + "null"); } builder.append(" & "); if (currentNode.rightChild != null) { builder.append(currentNode.data + "->" + currentNode.rightChild.data); childNodes.add(currentNode.rightChild); } else { builder.append(currentNode.data + "<-" + "null"); } builder.append(" | "); if (i == parentNodes.size() - 1) { System.out.println(builder.toString()); builder = new StringBuilder(); parentNodes = new ArrayList<Node<T>>(childNodes); childNodes = new ArrayList<Node<T>>(); i = -1; } } } }
测试,创建一个二叉搜索树(如下图)
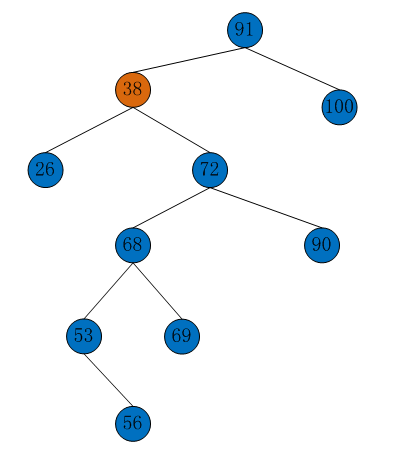
Tree<Integer> binaryTree=new BinaryTree<Integer>(); binaryTree.insert(new Node<Integer>(91)); binaryTree.insert(new Node<Integer>(38)); binaryTree.insert(new Node<Integer>(100)); binaryTree.insert(new Node<Integer>(26)); binaryTree.insert(new Node<Integer>(72)); binaryTree.insert(new Node<Integer>(90)); binaryTree.insert(new Node<Integer>(68)); binaryTree.insert(new Node<Integer>(69)); binaryTree.insert(new Node<Integer>(53)); binaryTree.insert(new Node<Integer>(56)); binaryTree.print();
打印结果如下:
-------------------------------------------------------------------------------- root:91 91<-38 & 91->100 | 38<-26 & 38->72 | 100->null & 100<-null | 26->null & 26<-null | 72<-68 & 72->90 | 68<-53 & 68->69 | 90->null & 90<-null | 53->null & 53->56 | 69->null & 69<-null | 56->null & 56<-null |
删除节点字值为“38”的节点:
binaryTree.delete(38);
binaryTree.print();
打印结构如下:
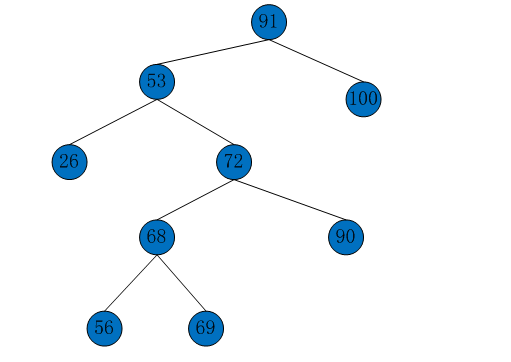
-------------------------------------------------------------------------------- root:91 91<-53 & 91->100 | 53<-26 & 53->72 | 100->null & 100<-null | 26->null & 26<-null | 72<-68 & 72->90 | 68<-56 & 68->69 | 90->null & 90<-null | 56->null & 56<-null | 69->null & 69<-null |
实其结构如下图:
8、二叉树效率
在查找过程中,需要访问每层的一个节点,所以只要知道有多少层就可以知道这些操作需要多长时间了。假设一棵满树,下图显示的就是容纳下给定数量节点所需要层数。

二叉搜索树比较的次数大致是数组中数据项个数的以2为底数的对数。设定节点个数为N,层数为L,则N比2的L此房小1,即:
N=2-1等于N+1=2,则L=log2(N+1)
因此,常见的树的操作时间复杂度大致是N以2为底的对数。在大O表示法中,表示为O(logN),如果树不满,分析起来就很困难。不过,可以认为对给定层数的树,不满的树的平均查找时间比满树要短。
把树和前边讲过的那些数据结构比较。在有1000000个数据项的无序数组或链表中,查找数据项平均会比较500000次,但在有1000000个节点的树(二叉搜索树)中,只需要20(或更少)次的比较。
有序数组可以很快的找到数据项,打插入的数据项平均要移动500000个数据项。在1000000个节点的树中插入数据项需要20次或更少的比较,再加上很短的时间来连接数据项。
同样,从有1000000个数据项的数组中删除一个数据项需要平均移动500000个数据项,而在1000000个节点的树中删除节点只需要20次或更少的比较来找到它,再加上(可能的话)一点比较的时间来找到它的后继节点,一点时间来断开这个节点的连接,以及连接它的后继。
因此,树对所有常用的数据存储操作都有很高的效率。
遍历不如其他的数据结构操作快。但是,遍历在大型数据库中不是常用的操作。它更常用于程序中的辅助方法来解析或其他的表达式,而且表达式一般都不会很长。
9、用数组表示树
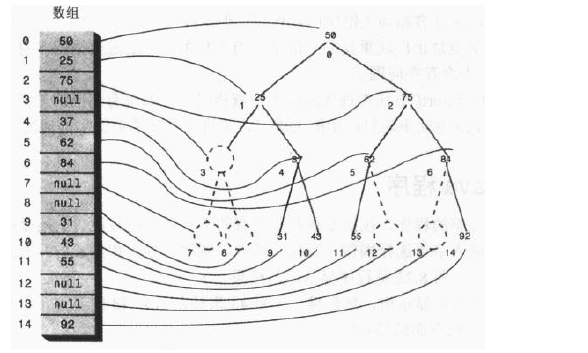
10.重复关键字
有重复关键字的节点都插入到与它的关键字相同的节点的右子节点出。
问题是find()方法只能找到两个(或多个)相同关键字节点中的第一个。可以修改find()方法来查找更多的数据项,区分有相同关键字的数据项,但这样很(至少有点)消耗时间。
可以选择禁止出现重复的关键字,当重复关键字通过数据的本身被排除了(例如,员工代码的数字),就不会存在问题了。
参考
摘抄《Java数据结构和算法.(第二版)》