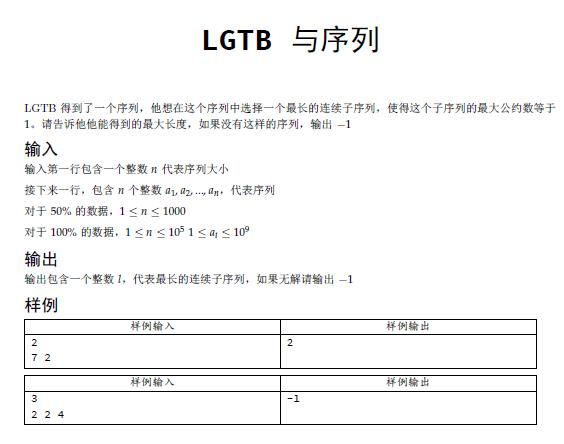
第一题存在的意义是送分。。(真的没有见过这么简单的数论题,想出正解来了还觉得是错的)
求序列的gcd,如果求出来是1,结果是n,否则是-1
1 #include<iostream> 2 #include<cstdio> 3 #include<cctype> 4 #include<cstring> 5 #include<cstdlib> 6 #include<fstream> 7 #include<sstream> 8 #include<algorithm> 9 #include<map> 10 #include<set> 11 #include<queue> 12 #include<vector> 13 #include<stack> 14 #include<cmath> 15 using namespace std; 16 typedef bool boolean; 17 #define INF 0xfffffff 18 #define smin(a, b) a = min(a, b) 19 #define smax(a, b) a = max(a, b) 20 template<typename T> 21 inline void readInteger(T& u){ 22 char x; 23 int aFlag = 1; 24 while(!isdigit((x = getchar())) && x != '-'); 25 if(x == '-'){ 26 x = getchar(); 27 aFlag = -1; 28 } 29 for(u = x - '0'; isdigit((x = getchar())); u = (u << 1) + (u << 3) + x - '0'); 30 ungetc(x, stdin); 31 u *= aFlag; 32 } 33 34 template<typename T> 35 T gcd(T a, T b){ 36 if(b == 0) return a; 37 return gcd(b, a % b); 38 } 39 40 int n; 41 int temp; 42 43 inline void init(){ 44 readInteger(n); 45 for(int i = 1, x; i <= n; i++){ 46 readInteger(x); 47 if(temp == 0) temp = x; 48 else temp = gcd(temp, x); 49 if(temp == 1) break; 50 } 51 } 52 53 inline void solve(){ 54 if(temp == 1) printf("%d", n); 55 else printf("-1"); 56 } 57 58 int main(){ 59 freopen("seq.in", "r", stdin); 60 freopen("seq.out", "w", stdout); 61 init(); 62 solve(); 63 return 0; 64 }
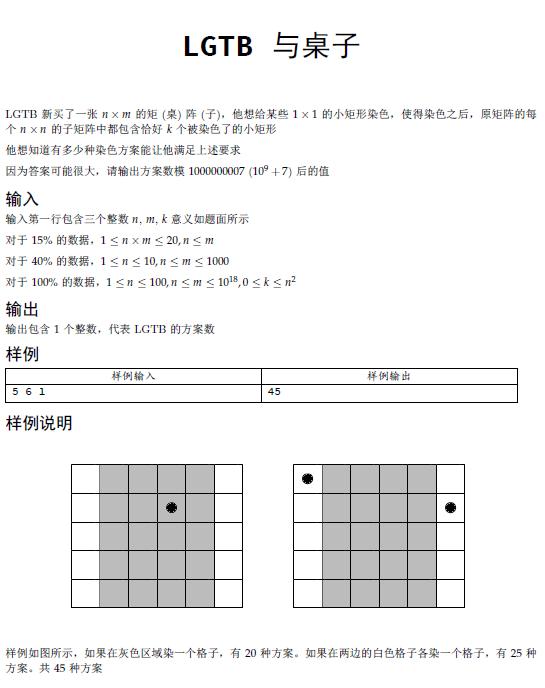
首先呢,随便画个一个很长很长的矩(长)阵(方形),然后随便画一画(手动枚举)。然后就可以发现前n列的情况和前n + 1到前2n的情况很类似,所以可以对每n列进行一次分区。当然,这就会出现一个问题,就是最后余下的几列。再看看样例,样例余下的一列和第i列情况是一样的。
分区以后,无论是空间还是时间都能够达到dp所能够承受的范围,于是用f[i][j](鼠标移到上面有惊喜)来完成dp,dp方程很容易推出:
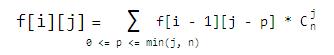
1 #include<iostream> 2 #include<cstdio> 3 #include<cctype> 4 #include<cstring> 5 #include<cstdlib> 6 #include<cmath> 7 #include<fstream> 8 #include<sstream> 9 #include<algorithm> 10 #include<map> 11 #include<set> 12 #include<queue> 13 #include<vector> 14 #include<stack> 15 using namespace std; 16 typedef bool boolean; 17 #define INF 0xfffffff 18 #define smin(a, b) a = min(a, b) 19 #define smax(a, b) a = max(a, b) 20 template<typename T> 21 inline void readInteger(T& u){ 22 char x; 23 int aFlag = 1; 24 while(!isdigit((x = getchar())) && x != '-'); 25 if(x == '-'){ 26 x = getchar(); 27 aFlag = -1; 28 } 29 for(u = x - '0'; isdigit((x = getchar())); u = (u << 1) + (u << 3) + x - '0'); 30 ungetc(x, stdin); 31 u *= aFlag; 32 } 33 34 template<typename T> 35 inline void putInteger(T u){ 36 if(u == 0){ 37 putchar('0'); 38 return; 39 } 40 if(u < 0){ 41 putchar('-'); 42 u *= -1; 43 } 44 stack<char> s; 45 while(u != 0) s.push(u % 10 + '0'), u /= 10; 46 while(!s.empty()) putchar(s.top()), s.pop(); 47 } 48 49 const int moder = 1000000007; 50 long long quick_pow(long long a, long long pos){ 51 if(pos == 1) return a; 52 long long temp = quick_pow(a, pos / 2); 53 if(pos & 1) return temp * temp % moder * a % moder; 54 return temp * temp % moder; 55 } 56 57 int n; 58 long long m; 59 int k; 60 long long c[2][102][102]; 61 62 inline void init(){ 63 readInteger(n); 64 readInteger(m); 65 readInteger(k); 66 c[0][0][0] = 1; 67 for(int i = 1; i <= n + 1; i++){ 68 for(int j = 1; j <= i; j++){ 69 c[0][i][j] = (c[0][i - 1][j - 1] + c[0][i - 1][j]) % moder; 70 } 71 } 72 long long pos = m / n; 73 for(int i = 1; i <= n + 1; i++){ 74 for(int j = 1; j <= i; j++){ 75 long long buf = c[0][i][j]; 76 c[0][i][j] = quick_pow(buf, pos); 77 c[1][i][j] = c[0][i][j] * buf % moder; 78 } 79 } 80 } 81 82 long long dp[101][10005]; 83 inline void solve(){ 84 int last = m % n; 85 int t = (last >= 1) ? (1) : (0); 86 for(int i = 0; i <= min(k, n); i++){ 87 dp[1][i] = c[t][n + 1][i + 1]; 88 } 89 for(int i = 2; i <= n; i++){ 90 t = (last >= i) ? (1) : (0); 91 dp[i][0] = 1; 92 for(int j = 1; j <= k && j <= i * n; j++){ 93 for(int l = 0; l <= min(n, j); l++){ 94 (dp[i][j] += dp[i - 1][j - l] * c[t][n + 1][l + 1] % moder) %= moder; 95 } 96 } 97 } 98 putInteger(dp[n][k]); 99 } 100 101 int main(){ 102 freopen("table.in", "r", stdin); 103 freopen("table.out", "w", stdout); 104 init(); 105 solve(); 106 return 0; 107 }

这道题并没什么特别有用的方法,正解两个大暴力+Hash表(笑)。
首先说说正解的核心思想吧,是数据分治,对于这道题有两种极端数据,一种是对于平行于y轴的点特别多(大约大于等于sqrt(n)),下面就把它叫做长链(树链剖分做多了?)吧,还有一种是特别少,下面就叫做短链吧。
对于短链来说,因为它条数多,但是每一条的数量少,所以直接大暴力枚举链中的两个点,再向后判断是否存在两个点使它们能够构成正方形。这样的时间复杂度为O(n*sqrt(n))也在承受范围之内。
对于长链来说,因为它条数少,但是每一条的数量多,如果还按照上面那种做法会很吃亏,所以就排个序,暴力枚举任意两条长链上纵坐标相等的两点(当然要有点技巧,要让它变成O(len))。这样的时间复杂度也在承受范围之内。
然后对于短链和长链之间的部分,貌似被忽略了,因为短链的数量更多一些,所以这个任务就交给短链,短链在暴力的过程中已经算过往后的点了,所以找长链就往前找了,接着做法和刚刚完全一样。
再说说判点,判断一个东西存不存在是不是想到了set,不过很遗憾地告诉你,如果用set的话,总时间复杂度就得加上一个$log n$,然后就T掉了一抹多的点。那么怎么让它接近O(1),方法就是Hash,自己建一个HashSet,用模质数+链表的方法来实现
1 #include<iostream> 2 #include<cstdio> 3 #include<cctype> 4 #include<cstring> 5 #include<cstdlib> 6 #include<fstream> 7 #include<sstream> 8 #include<algorithm> 9 #include<map> 10 #include<set> 11 #include<queue> 12 #include<vector> 13 #include<stack> 14 #include<cmath> 15 using namespace std; 16 typedef bool boolean; 17 #define INF 0xfffffff 18 #define smin(a, b) a = min(a, b) 19 #define smax(a, b) a = max(a, b) 20 template<typename T> 21 inline void readInteger(T& u){ 22 char x; 23 int aFlag = 1; 24 while(!isdigit((x = getchar())) && x != '-'); 25 if(x == '-'){ 26 x = getchar(); 27 aFlag = -1; 28 } 29 for(u = x - '0'; isdigit((x = getchar())); u = (u << 1) + (u << 3) + x - '0'); 30 ungetc(x, stdin); 31 u *= aFlag; 32 } 33 34 template<typename T> 35 class LinkTable{ 36 public: 37 int next; 38 T key; 39 LinkTable(){} 40 LinkTable(T key, int next):key(key), next(next){} 41 }; 42 43 template<typename T> 44 class HashSet { 45 private: 46 static const int moder = 4000007; 47 int hash(long long x){ 48 return (int)(x % moder); 49 } 50 public: 51 int s; 52 LinkTable<T> *list; 53 int* h; 54 HashSet():list(NULL), h(NULL), s(0){ } 55 HashSet(int size):s(0){ 56 list = new LinkTable<T>[(const int)(size + 1)]; 57 h = new int[moder + 1]; 58 memset(h, 0, sizeof(h) * (moder + 1)); 59 } 60 void insert(T x){ 61 int hashcode = hash(x); 62 list[++s] = LinkTable<T>(x, h[hashcode + 1]); 63 h[hashcode + 1] = s; 64 } 65 boolean count(T x){ 66 int hashcode = hash(x); 67 for(int i = h[hashcode + 1]; i != 0; i = list[i].next){ 68 if(list[i].key == x) 69 return true; 70 } 71 return false; 72 } 73 }; 74 75 int n; 76 vector<int> p[100001]; 77 vector<int> small; //数据分治 78 vector<int> big; 79 HashSet<long long> hs; 80 81 const long long dou = 100003; 82 inline long long toLong(int x, int y){ 83 return x * dou + y * 2; 84 } 85 86 inline void init(){ 87 readInteger(n); 88 hs = HashSet<long long>(n); 89 for(int i = 1, a, b; i <= n; i++){ 90 readInteger(a); 91 readInteger(b); 92 p[a].push_back(b); 93 hs.insert(toLong(a, b)); 94 } 95 } 96 97 int seg; 98 inline void div(){ 99 seg = (int)sqrt(n + 0.5); 100 for(int i = 0; i <= 100000; i++){ 101 if((signed)p[i].size() >= seg) 102 big.push_back(i); 103 else if((signed)p[i].size() > 0) 104 small.push_back(i); 105 } 106 } 107 108 int result = 0; 109 inline void solve_small(){ 110 for(int i = 0; i < (signed)small.size(); i++){ 111 int row = small[i]; 112 for(int j = 0; j < (signed)p[row].size() - 1; j++){ 113 for(int k = j + 1; k < (signed)p[row].size(); k++){ 114 int y1 = p[row][j], y2 = p[row][k]; 115 int len = abs(y1 - y2); 116 int x1 = row + len; 117 int x2 = row - len; 118 boolean check1 = hs.count(toLong(x1, y1)); 119 boolean check2 = hs.count(toLong(x1, y2)); 120 if(check1 && check2) result++; 121 if(x2 >= 0 && (signed)p[x2].size() >= seg){ 122 check1 = hs.count(toLong(x2, y1)); 123 check2 = hs.count(toLong(x2, y2)); 124 if(check1 && check2) result++; 125 } 126 } 127 } 128 } 129 } 130 131 inline void solve_big() { 132 for(int i = 0; i < (signed)big.size(); i++){ 133 int s = big[i]; 134 if(p[s].size() > 0) 135 sort(p[s].begin(), p[s].end()); 136 } 137 for(int i = 0; i < (signed)big.size() - 1; i++){ 138 for(int j = i + 1; j < (signed)big.size(); j++){ 139 int r1 = big[i], r2 = big[j]; 140 int len = abs(r1 - r2); 141 int p1 = 0, p2 = 0; 142 while(p1 < (signed)p[r1].size() && p2 < (signed)p[r2].size()){ 143 if(p[r1][p1] == p[r2][p2]){ 144 int y1 = p[r1][p1]; 145 boolean check1 = hs.count(toLong(r1, y1 + len)); 146 boolean check2 = hs.count(toLong(r2, y1 + len)); 147 if(check1 && check2) result++; 148 p1++, p2++; 149 }else if(p[r1][p1] > p[r2][p2]) p2++; 150 else p1++; 151 } 152 } 153 } 154 } 155 156 int main(){ 157 freopen("square.in", "r", stdin); 158 freopen("square.out", "w", stdout); 159 init(); 160 div(); 161 solve_small(); 162 solve_big(); 163 printf("%d", result); 164 return 0; 165 }