描述
一条单向的铁路线上,依次有编号为 1, 2, ..., n 的 n 个火车站。每个火车站都有一个级别,最低为 1 级。现有若干趟车次在这条线路上行驶,每一趟都满足如下要求:如果这趟车次停靠了火车站 x,则始发站、终点站之间所有级别大于等于火车站 x 的都必须停靠。
(注意:起始站和终点站自然也算作事先已知需要停靠的站点)
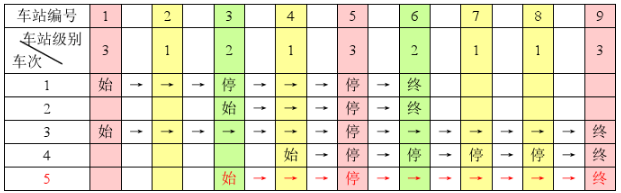
例如,下表是 5 趟车次的运行情况。其中,前 4 趟车次均满足要求,而第 5 趟车次由于停靠了 3 号火车站(2 级)却未停靠途经的 6 号火车站(亦为 2 级)而不满足要求。
现有 m 趟车次的运行情况(全部满足要求),试推算这 n 个火车站至少分为几个不同的级别。
格式
输入格式
第一行包含 2 个正整数 n, m,用一个空格隔开。
第 i + 1 行(1 ≤ i ≤ m)中,首先是一个正整数 s i (2 ≤ s i ≤ n),表示第 i 趟车次有 s i 个停靠站;接下来有 s i 个正整数,表示所有停靠站的编号,从小到大排列。每两个数之间用一个空格隔开。输入保证所有的车次都满足要求。
输出格式
输出只有一行,包含一个正整数,即 n 个火车站最少划分的级别数。
样例1
样例输入1
9 2
4 1 3 5 6
3 3 5 6
样例输出1
2
样例2
样例输入2
9 3
4 1 3 5 6
3 3 5 6
3 1 5 9
样例输出2
3
限制
每个测试点1s。
提示
对于 20%的数据,1 ≤ n, m ≤ 10;
对于 50%的数据,1 ≤ n, m ≤ 100;
对于 100%的数据,1 ≤ n, m ≤ 1000
来源
NOIP 2013 普及组
题目大意 (题目很简洁,不需(会)要(写)大意)
显然拓扑排序。(哪来那么多显然?)
这是一个拓扑排序比较基本的应用吧。
现在考虑如何建图,首先确定节点u连向节点v的一条有向边表示什么,表示v比u的等级高(严格大于)。
那么拓扑排序进行了多少层就是答案了。
因为从起点到终点间停靠的站的等级大于等于这两个站,所以不确定,不能连边,但是,中间没有停靠的站一定比这些停靠了的站等级低,故这中间所有没有停靠的站,向所有停靠了的站连1条有向边。
然而这样很遗憾的是,理论上O(n3)是会TLE,所以我们需要一些黑科技优化。(但实际上,普及组的数据比较水。。。所以可以过)
我们直接考虑点i会向哪些点连边。首先我们需要枚举所有航线,如果这个点在它的起点和终点间,并且没有停靠,我们就需要向这些停靠的点连边。这个实质上是将一些需要连边的顶点集合取并,所以考虑bitset黑科技优化,来代替暴力连边。
因此总时间复杂度成功降为。就算是ccf老年机卡一卡就过去了。
(这里不得不吐槽一下洛谷的评测鸡真的是ccf老年机标配,洛谷上跑bitset优化后的程序和在vijos和codevs上跑n3大暴力的时间差不多,不过记事本一遍A真地很开心,一个编译错误都没有)
Code
1 /** 2 * luogu 3 * Problem#1983 4 * Accepted 5 * Time: 764ms 6 * Memory: 12132k 7 */ 8 #include <bits/stdc++.h> 9 using namespace std; 10 #define smax(a, b) a = max(a, b) 11 12 int n, m; 13 bitset<1001> *g; 14 bitset<1001> *stop; 15 int *ss, *st; 16 17 inline void init() { 18 scanf("%d%d", &n, &m); 19 g = new bitset<1001>[(n + 1)]; 20 stop = new bitset<1001>[(m + 1)]; 21 ss = new int[(m + 1)]; 22 st = new int[(m + 1)]; 23 for(int i = 1, c, t; i <= m; i++) { 24 scanf("%d%d", &c, &ss[i]); 25 c -= 2; 26 stop[i][ss[i]] = 1; 27 while(c--) { 28 scanf("%d", &t); 29 stop[i][t] = 1; 30 } 31 scanf("%d", st + i); 32 stop[i][st[i]] = 1; 33 } 34 } 35 36 int *dag; 37 int *dep; 38 queue<int> que; 39 inline void topu() { 40 for(int i = 1; i <= n; i++) 41 if(!dag[i]) 42 que.push(i), dep[i] = 1; 43 44 while(!que.empty()) { 45 int e = que.front(); 46 que.pop(); 47 for(int i = 1; i <= n; i++) { 48 if(!g[e][i]) continue; 49 dag[i]--, smax(dep[i], dep[e] + 1); 50 if(!dag[i]) que.push(i); 51 } 52 } 53 } 54 55 inline void solve() { 56 dag = new int[(n + 1)]; 57 dep = new int[(n + 1)]; 58 memset(dag, 0, sizeof(int) * (n + 1)); 59 memset(dep, 0, sizeof(int) * (n + 1)); 60 for(int i = 1; i <= n; i++) { 61 for(int j = 1; j <= m; j++) 62 if(i >= ss[j] && i <= st[j] && !stop[j][i]) 63 g[i] |= stop[j]; 64 for(int j = 1; j <= n; j++) 65 if(g[i][j]) 66 dag[j]++; 67 } 68 topu(); 69 int res = 0; 70 for(int i = 1; i <= n; i++) 71 smax(res, dep[i]); 72 printf("%d ", res); 73 } 74 75 int main() { 76 init(); 77 solve(); 78 return 0; 79 }