名词:
型数:看积分环节的个数
阶数:看分母s的指数
线性时不变系统:
叠加性
输入的叠加等于输出的叠加
非本质非线性可以用线性进行近视求解
本质非线性只能使用非线性进行解决,目前还是比较难解决
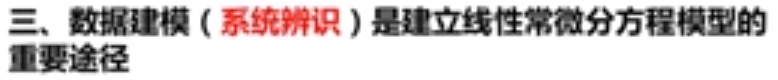
一个函数的傅里叶变化可能是发散的 (判断条件 :狄利克雷条件)
拉普拉斯变化是求解微分方程的利器
拉普拉斯变换是从傅里叶变换那里来的 就是增加一个衰减因子
拉普拉斯 对应复频域 傅里叶变换对应频域
常见的拉普拉斯变换:
拉普拉斯变换的主要性质:
使用这些变换可以方便的求解一些其他的函数
微分性质

中值定理:

初值定理和终值定理是相对的

这个表记住:

希望将拉普拉斯变换常用于求解微分方程中
不仅能够求解系统的动态性能,还要能进行改进,那么改进的出发点在哪呢?

这就是答案! 这是第一次打招呼 以后还是要经常见的呦!!! 下面见识一下他的威力吧,以免被吓到!!!



动态系统的描述方式(除微分方程外):传递函数模型
传递函数就是微分方程的替代品 : 可以方便直观的进行表示 知道输入 再知道传递函数就知道输出了
求解方程的半成品: 这一部分并没有进行求解微分方程



传递函数的特征量:

各种常见的环节:
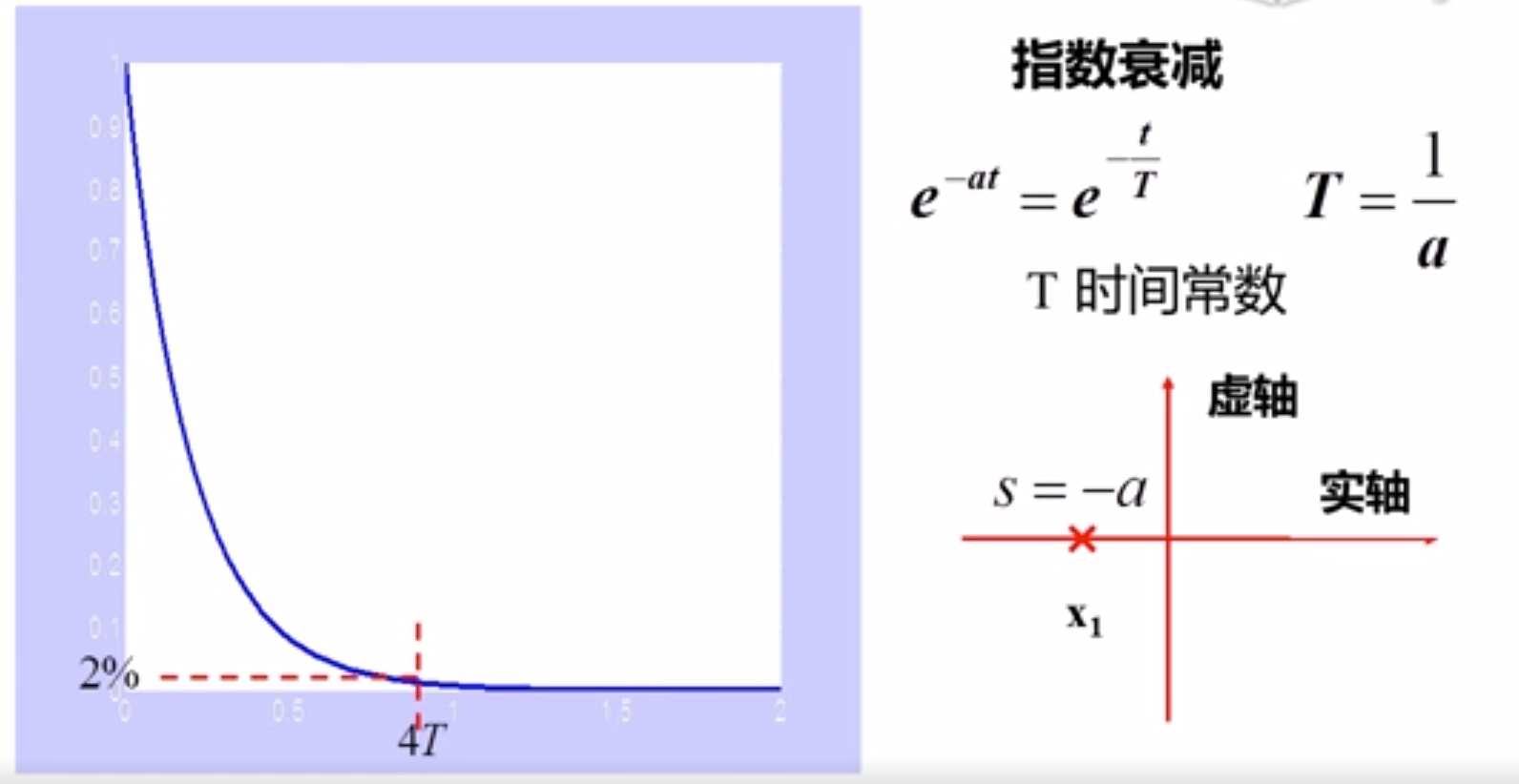
比例环节:

应用实例:
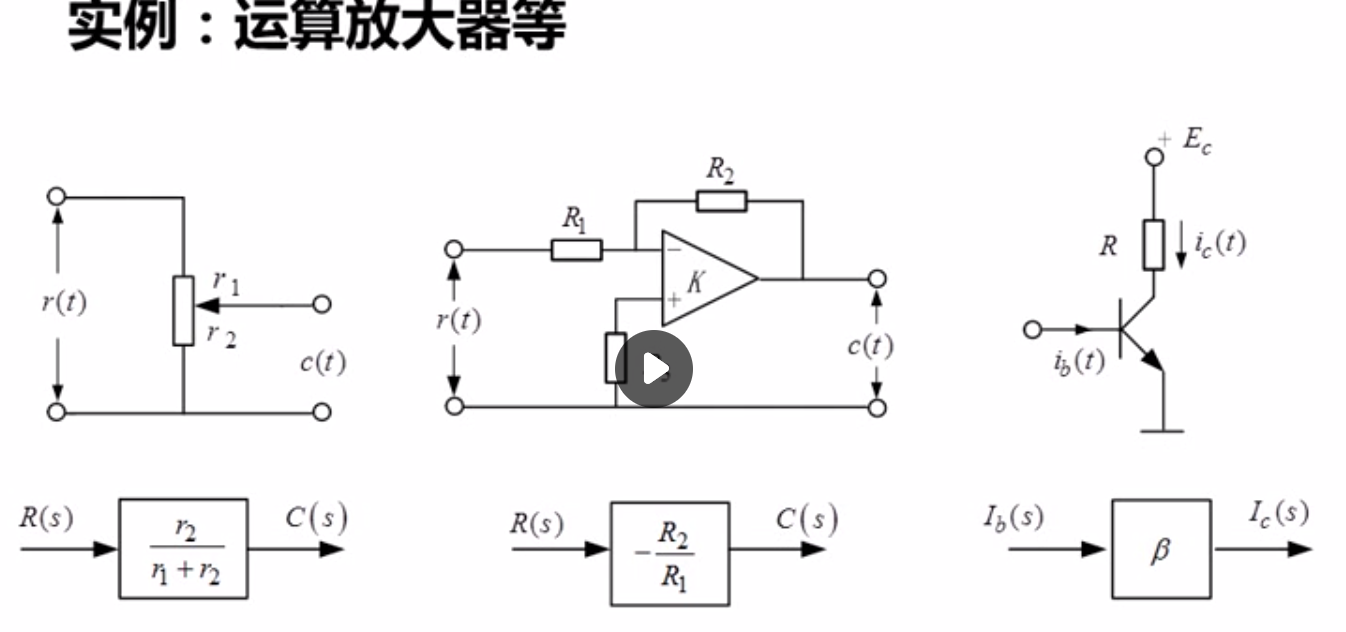
微分环节:

应用实例:
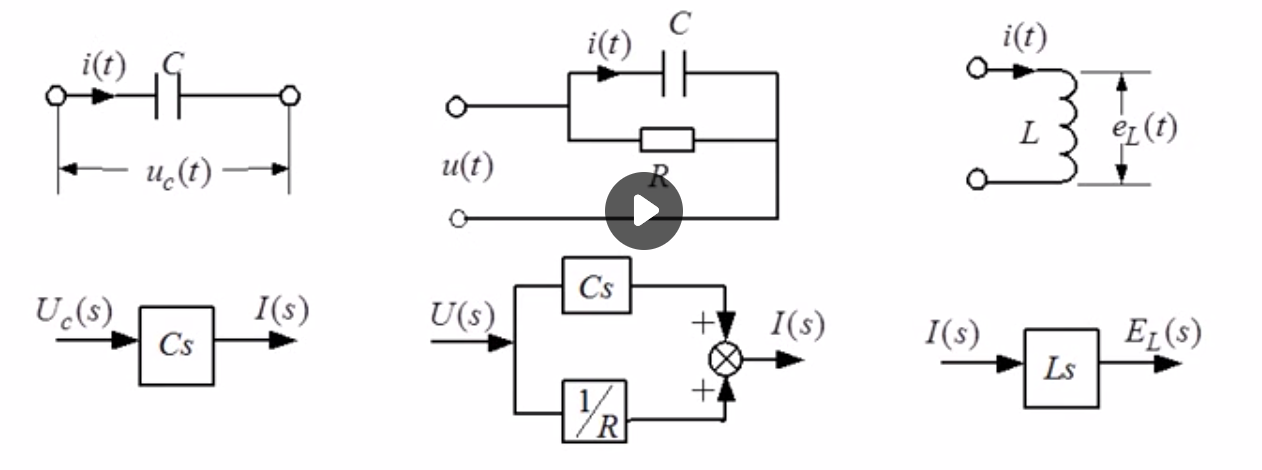
积分环节:

应用实例: 里程计 第一个就是这个原理 输出量为速度 输入量为转速
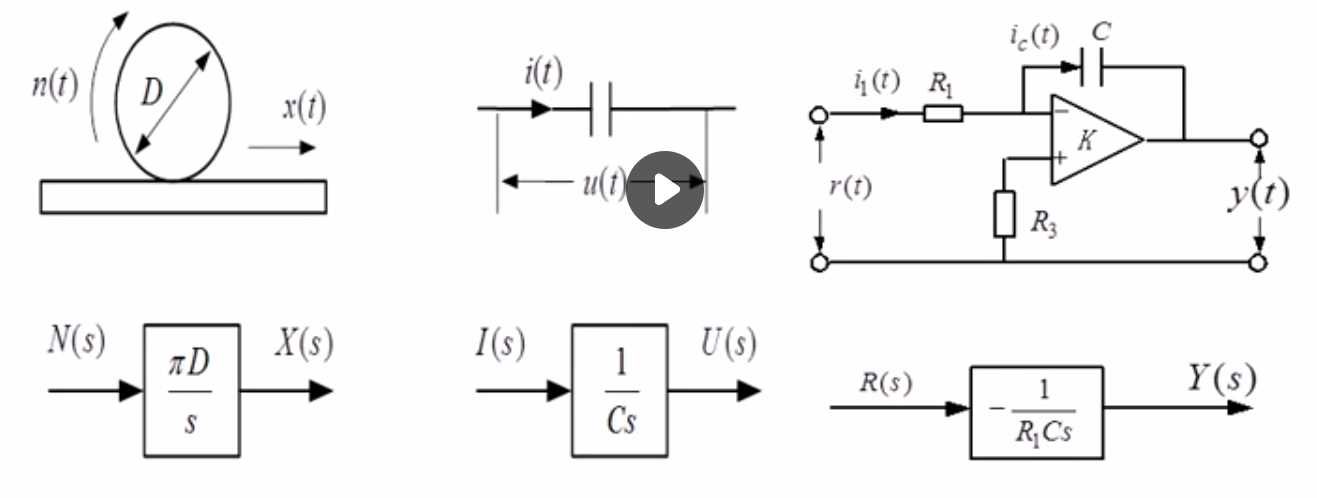
惯性环节: 低通滤波器
应用实例:
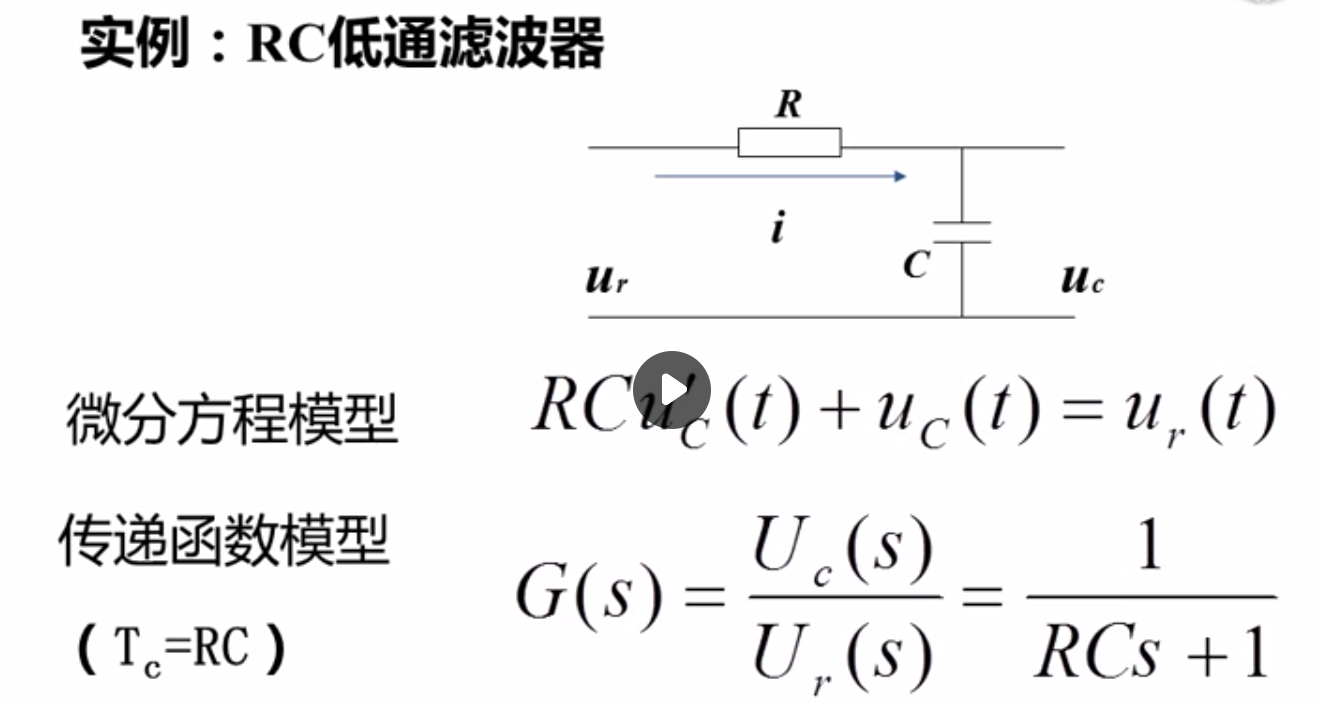

电容两端的电压不是加上电压之后就直接有电压了,而是缓慢的上升
二阶振荡环节:

应用实例:
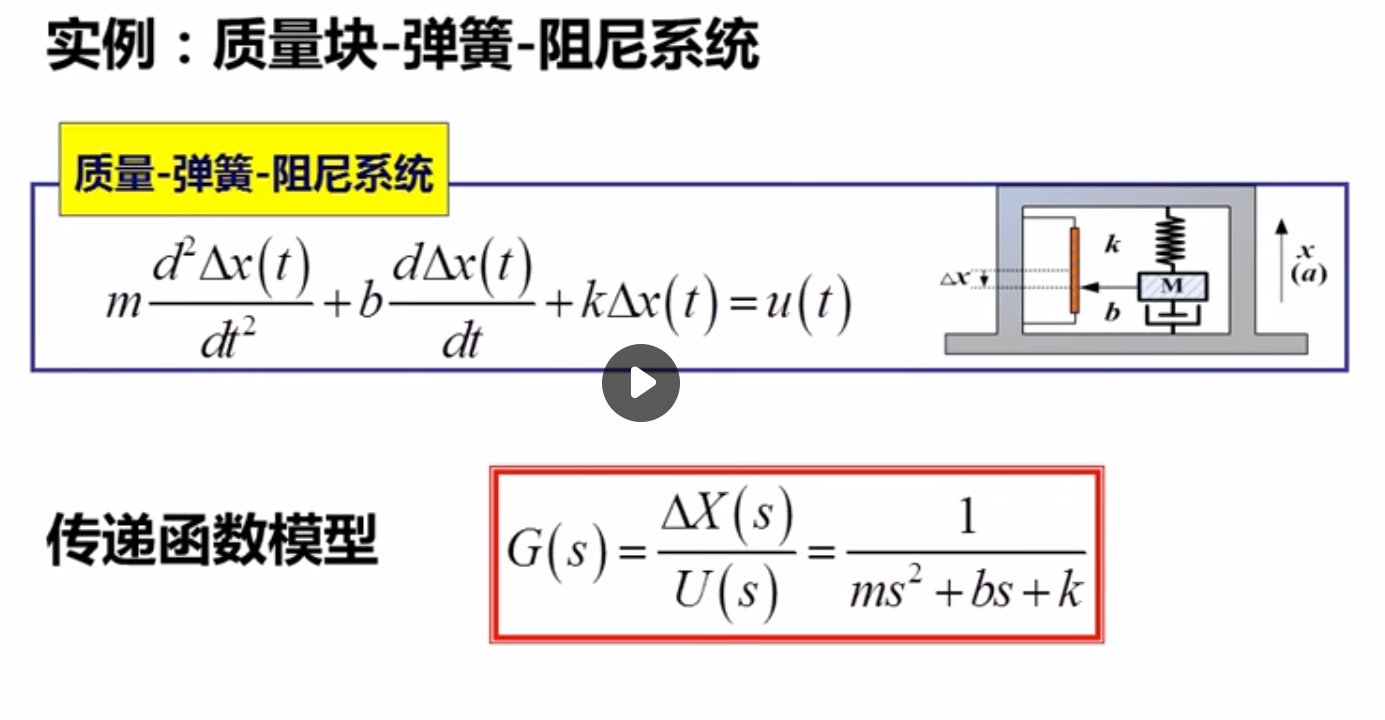
比例微分环节:

二阶微分环节:

小结:


信号线:
引出点:
比较点:
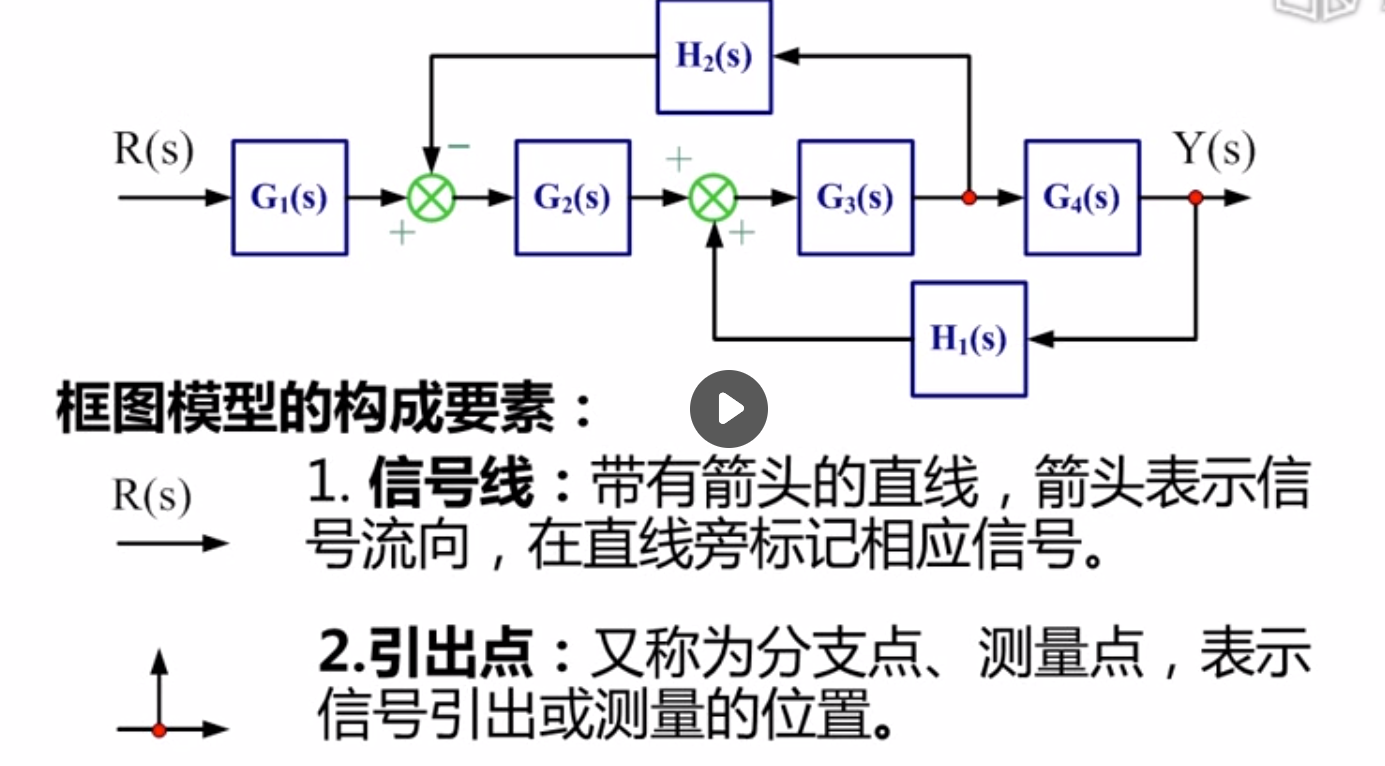
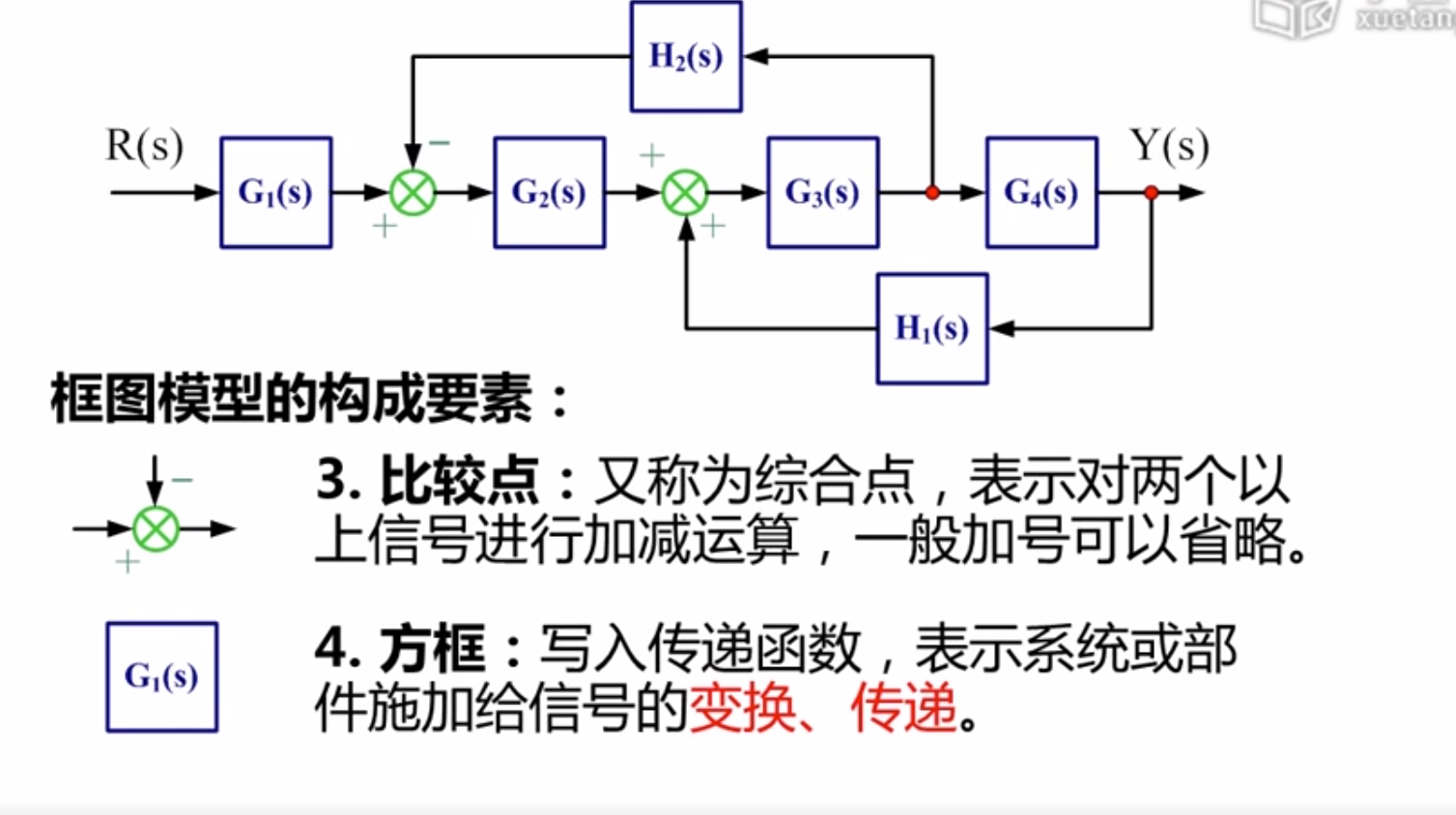

想要知道细节就要知道具体的框图
框图化简:原则:化简前后代数等效
化简原则:
1,轻易不要改变比较点的顺序
2,
框图化简涉及到简化的部分,但是如何直接能看到系统的传递函数呢?
信号流图:

前向通路:

不接触回路:



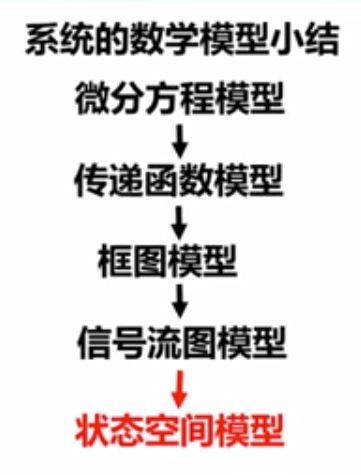
系统框图小结:
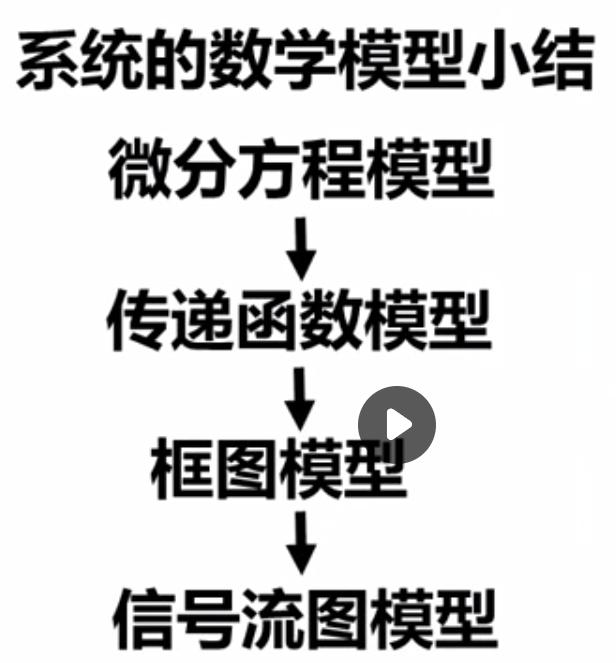
还有一个状态空间模型:
系统性能指标的评价:
常见的测试信号:

系统的瞬态响应和稳态响应
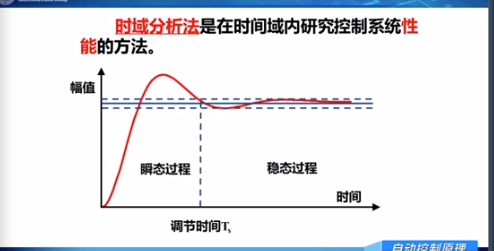

瞬态响应:





典型环节的系统响应:
一阶系统


T是这个系统中唯一一个性能参数:
一阶系统脉冲响应:
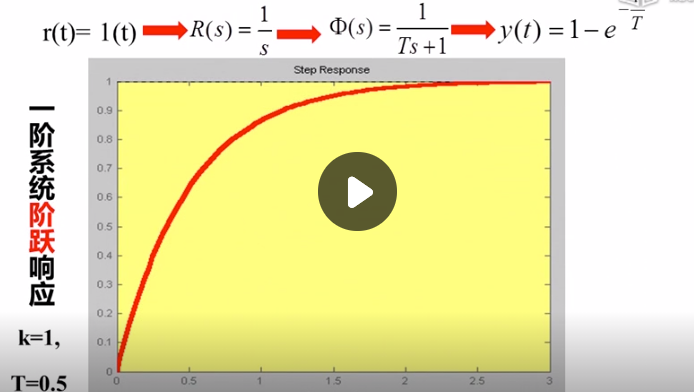
一阶系统阶跃响应:


一阶系统就是低通滤波器 也叫惯性器件
一阶系统斜坡响应:
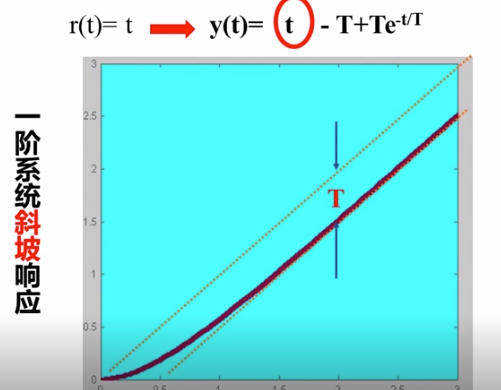
这个有固定的偏差,所以没有准确性
一阶系统的功能简单,改善性能的空间和手段有限。


二阶系统:目前工业上使用最多的系统
阻尼系数和自然频率是两个重要的系数
根据标准二阶系统求解各种参数:




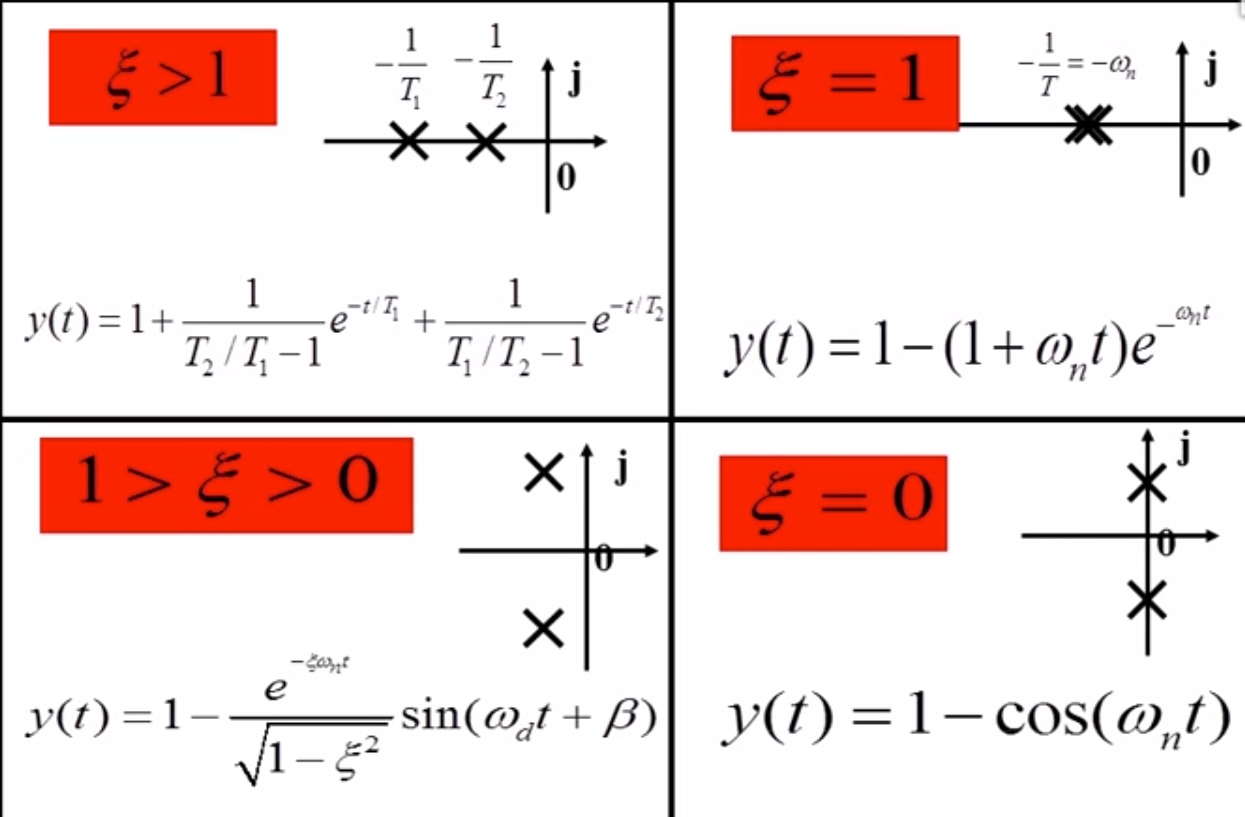
二阶系统的参数调节:
极点的位置和系统的参数密切相关
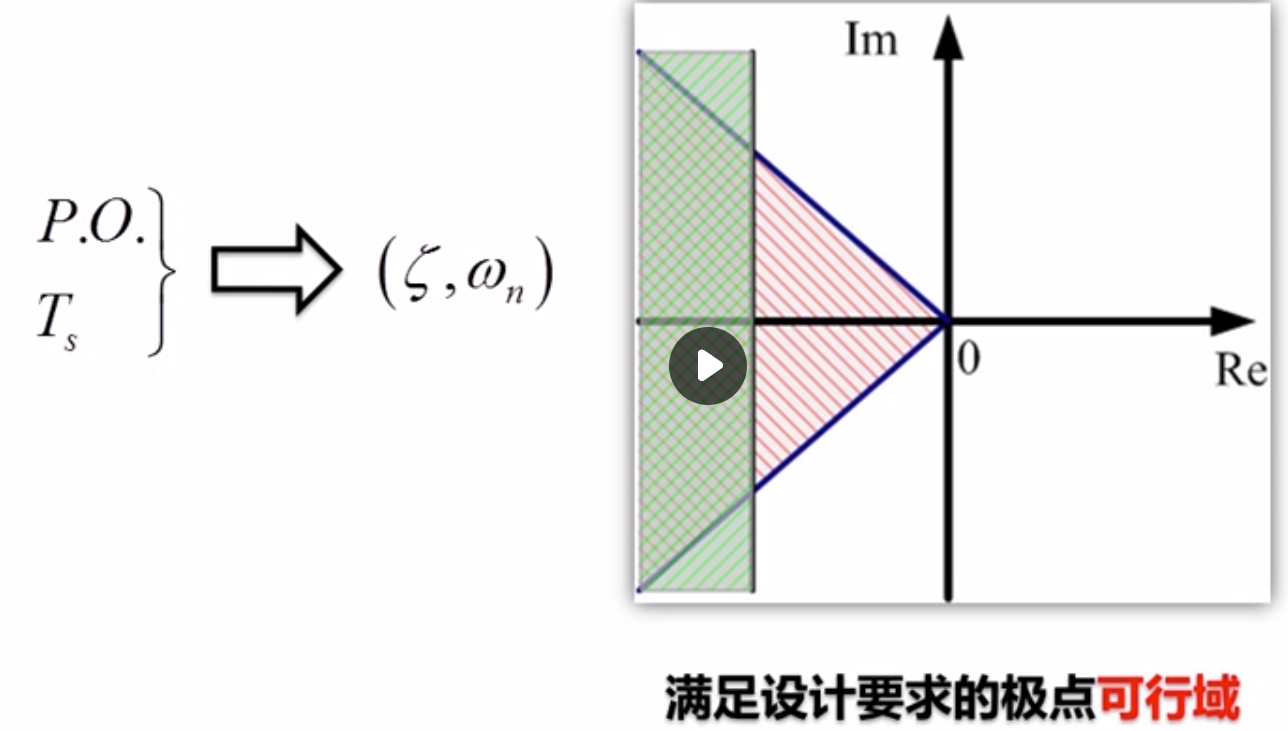
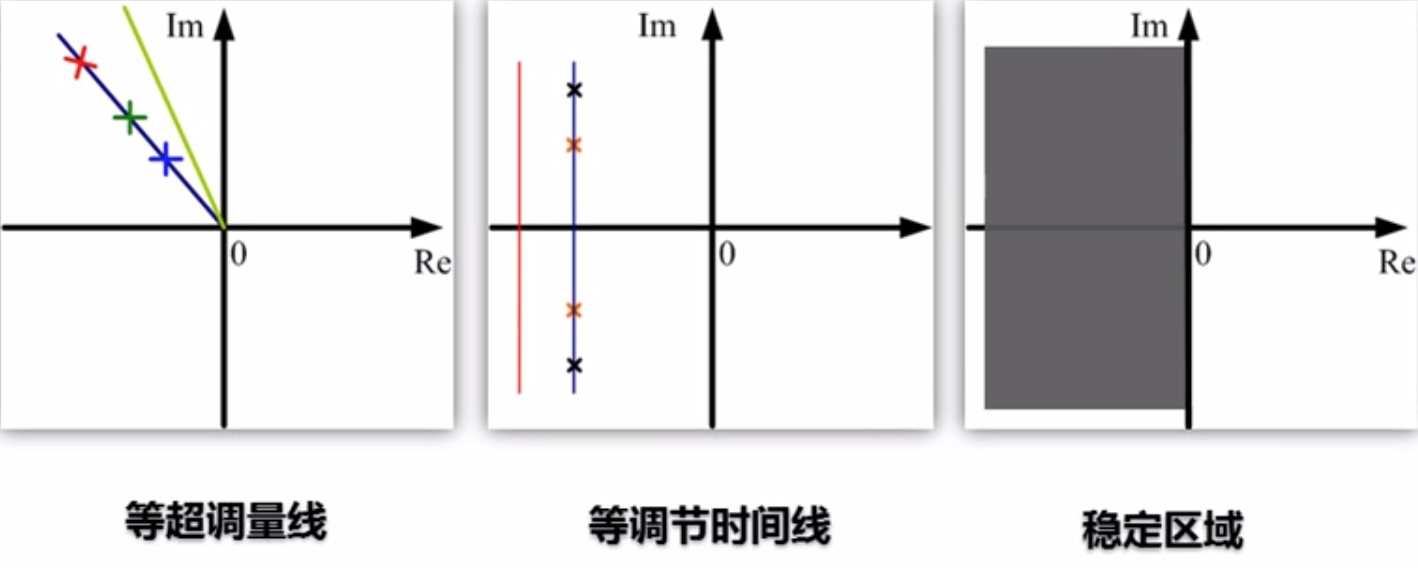
有各种等阻尼线
满足性能 的可行域
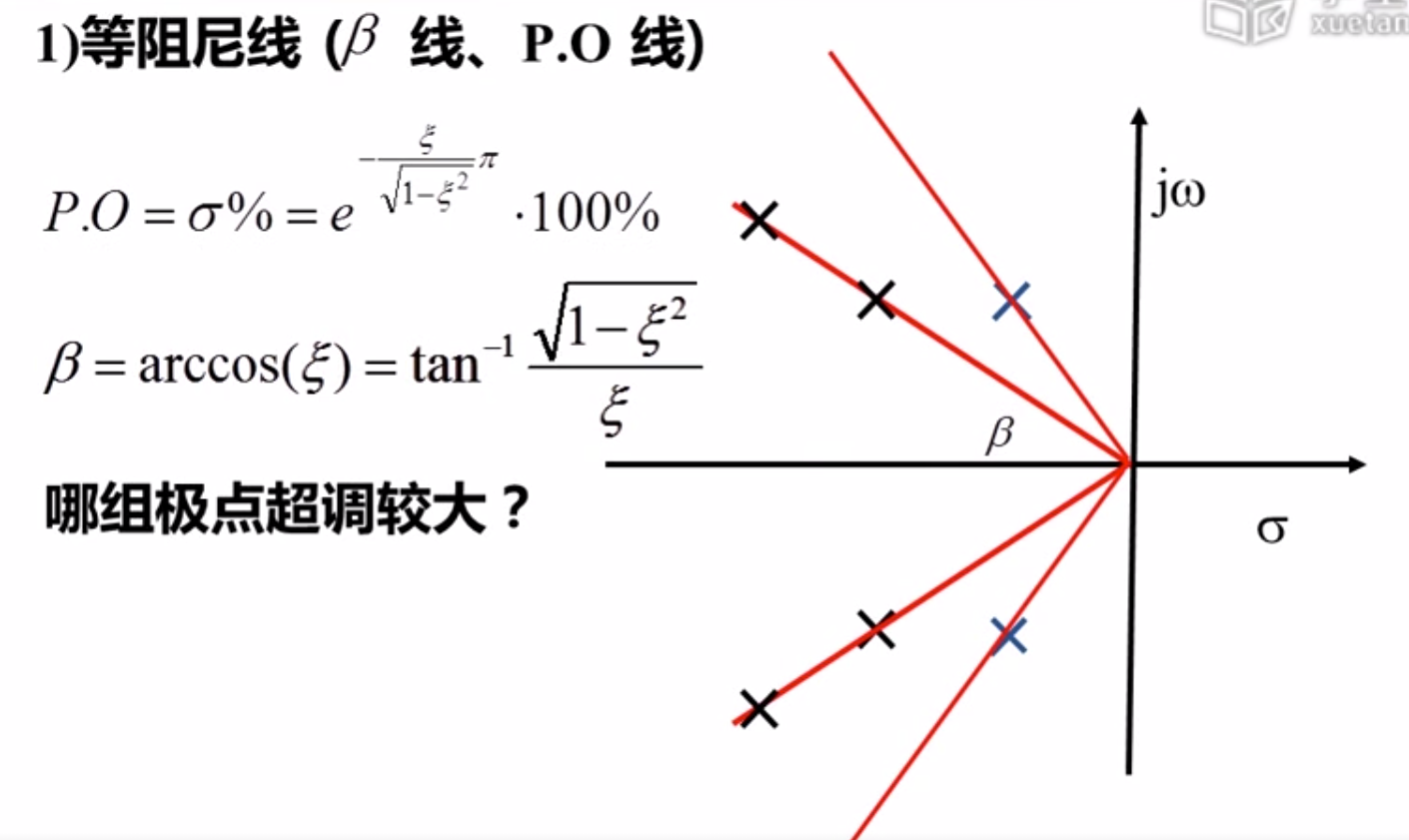
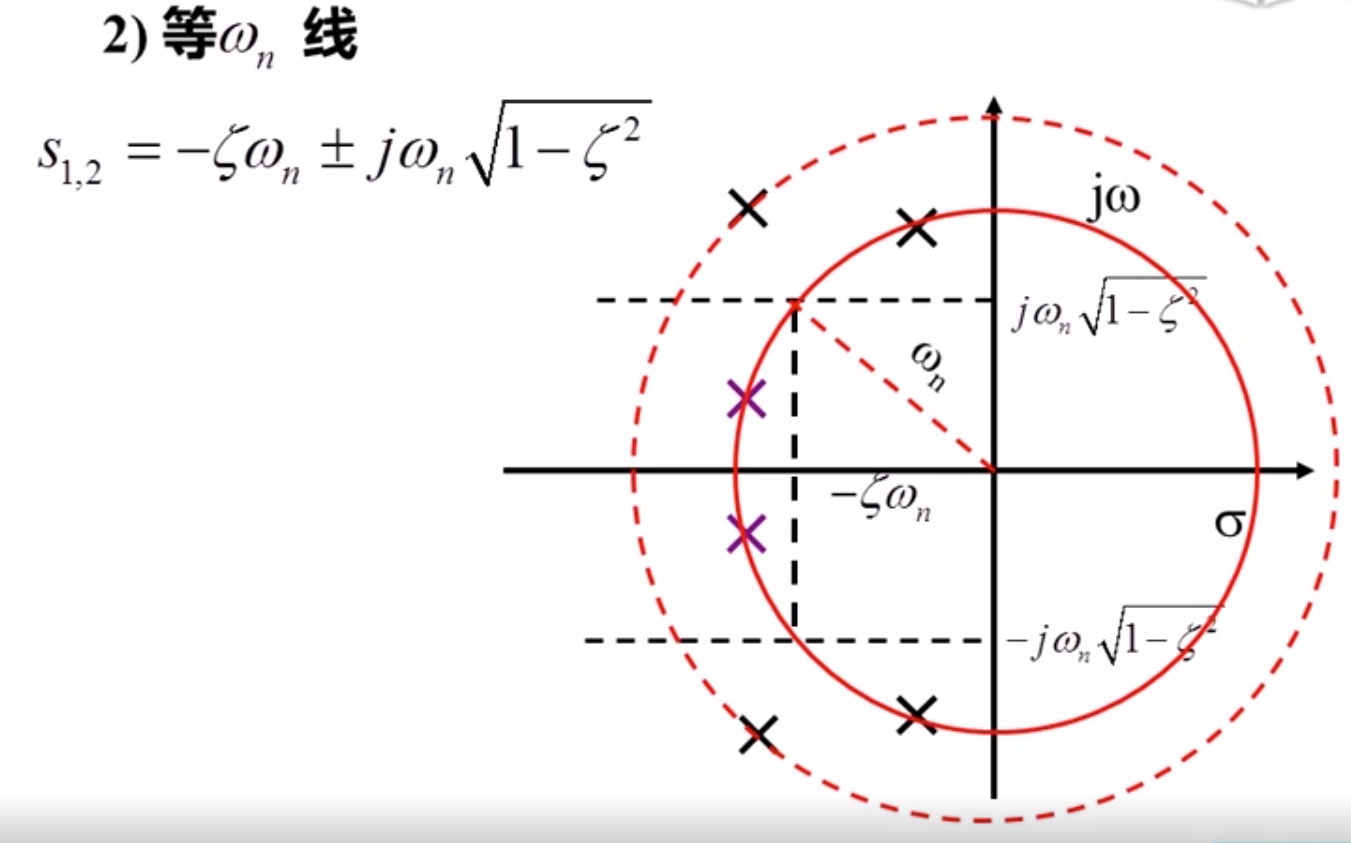
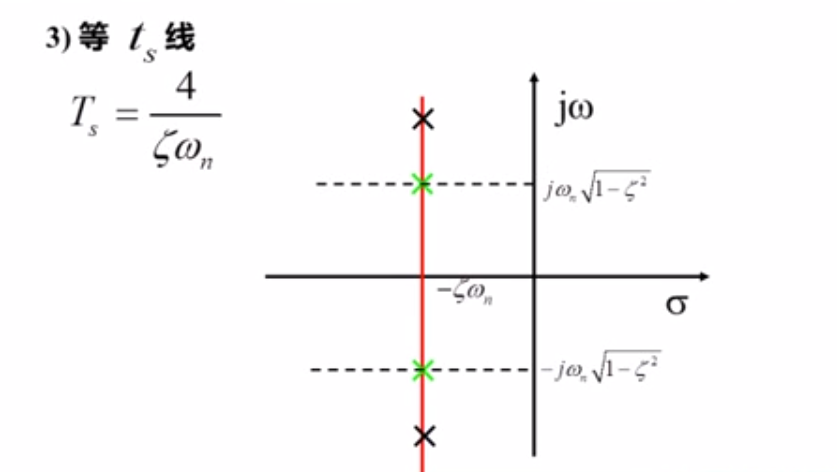

二营长,炮楼那个倒了!!!
系统的稳准狠的参数,并且可以进行参数的调节 ,并能进行稳定性判断,劳施判据
根轨迹法:一定是闭环的根轨迹,没有开环的根轨迹这样的说法。是开环系统某一参数(例如开环增益k)从零变化到无穷时,闭环系统特征方程的根在s平面上变化的轨迹
详细教程参考博文:https://blog.csdn.net/qq_45379724/article/details/109691614?ops_request_misc=&request_id=&biz_id=102
还有就是卢京潮老师将的比较好 https://www.bilibili.com/video/BV1ZJ411c757?p=25
当某一个参数变化的时候,极点是怎么变化的
例如:

根规矩解决的问题:解决参数在变化过程中 的根轨迹变化的过程,不用解很多的方程进行分析
例如下面的根轨迹的求法:
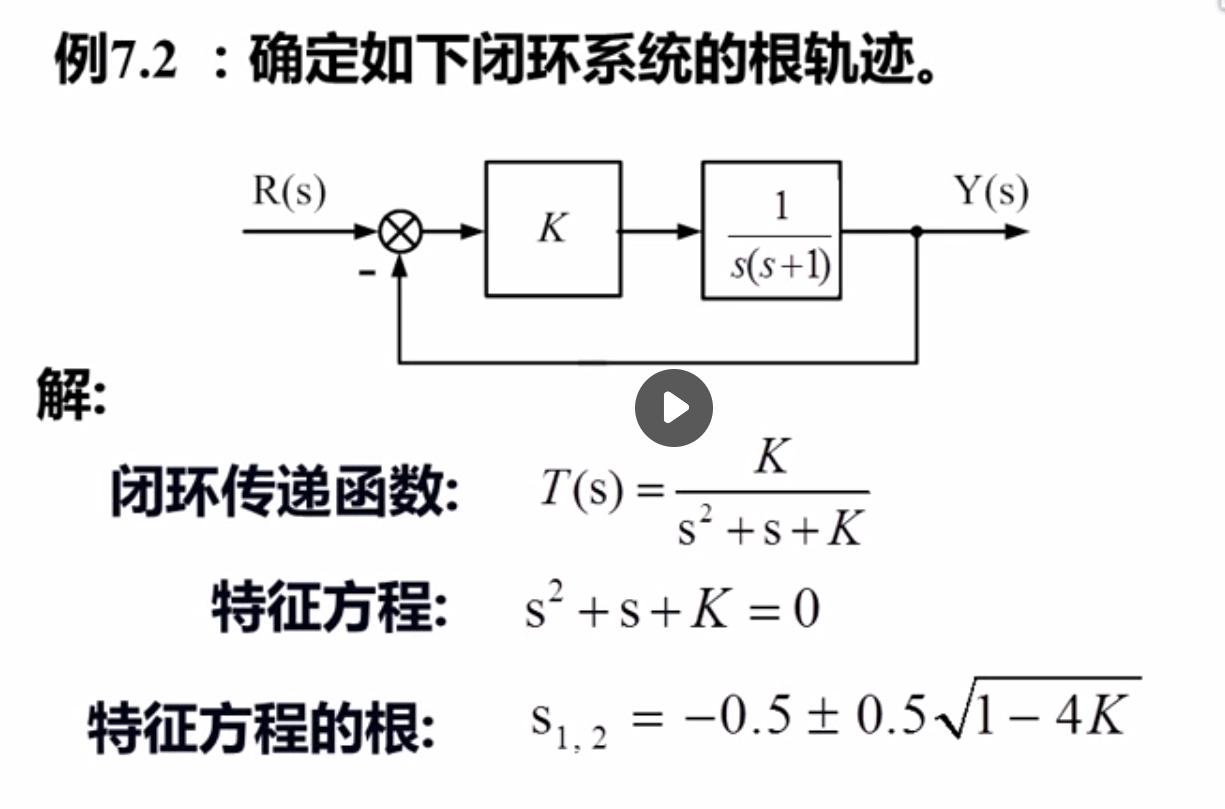
写出特征方程得根,然后进行绘图即可
根轨迹的绘制方法:详细教程参考:https://blog.csdn.net/qq_45379724/article/details/109691614?ops_request_misc=&request_id=&biz_id=102




卢讲解了闭环极点变化(根轨迹)跟开环零极点的关系


分离点和汇合点的计算

这句话解释了分离点和汇合点的特点,可以把这个作为计算的依据
出射角和入射角计算
根轨迹法则:

利用根轨迹改善系统的性能
1,附加开环的零点极点
2,附加闭环的零点极点
用根轨迹进行系统的矫正的时候用频域法同样可以,并且用频域法更方便
频率响应
系统输出的幅值和相角随着输入w的改变而改变的情况

典型环节的乃圭斯特图:

步骤:
1,令s=jw 然后算出幅值和相角
2,绘制相关的曲线,哪一种都可以 根据需要来
要是有两个及以上的变量的话,那就固定其中一个变量,然后讨论另外一个变量的变化情况
谐振频率和峰值频率:

典型环节的幅频特性曲线:

频域稳定行判据



非线性系统:

上面那个式子就是线性定常系统,如果出现各阶导数的高次项,或者出现常数项,就不是线性系统了,就是非线性系统

幅值裕度和相角裕度
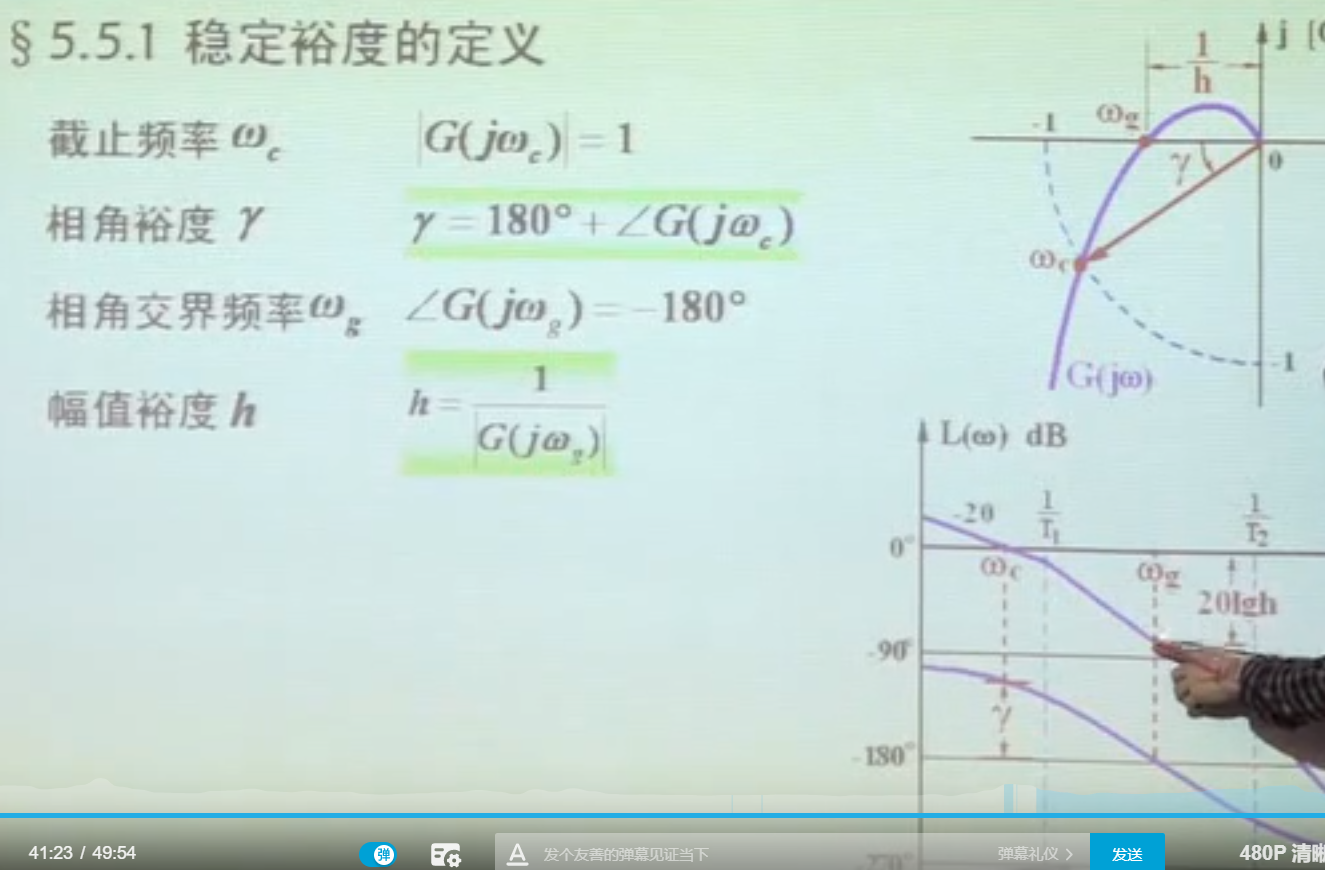

从低频段判断开环增益和系统型别
中频段就是截止频率附近的地方 决定系统的动态性能 所以可以重点分析中频段的情况
分析高频段可以判断系统抗高频干扰的能力
分析高频可以分析系统开环系统抗高频干扰的能力、进而可以分析闭环系统抗高频干扰的能力
最小相角系统:开环的零极点都在虚轴的左边或者虚轴上
系统校正:



串联超前矫正
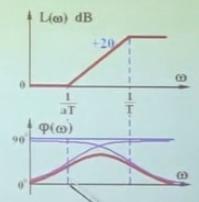
利用相角超前的特性,计算最大超前角的位置和值是多少
这个超前矫正能够提高相角裕度
现代控制系统:
状态空间
经典控制中的各种概念还能应用在现代控制系统中吗