足球比赛具有一定程度的偶然性,弱队也有战胜强队的可能。
假设有甲、乙、丙、丁四个球队。根据他们过去比赛的成绩,得出每个队与另一个队对阵时取胜的概率表:
甲 乙 丙 丁
甲 - 0.1 0.3 0.5
乙 0.9 - 0.7 0.4
丙 0.7 0.3 - 0.2
丁 0.5 0.6 0.8 -
数据含义:甲对乙的取胜概率为0.1,丙对乙的胜率为0.3,...
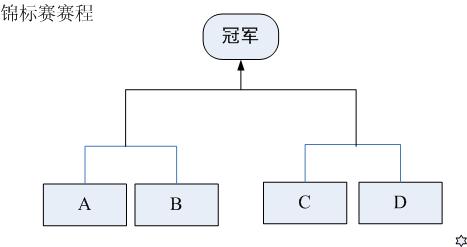
现在要举行一次锦标赛。双方抽签,分两个组比,获胜的两个队再争夺冠军。(参见【1.jpg】)
请你进行10万次模拟,计算出甲队夺冠的概率。
注意:
请仔细调试!您的程序只有能运行出正确结果的时候才有机会得分!
在评卷时使用的输入数据与试卷中给出的实例数据可能是不同的。
请把所有函数写在同一个文件中,调试好后,存入与【考生文件夹】下对应题号的“解答.txt”中即可。
相关的工程文件不要拷入。
源代码中不能能使用诸如绘图、Win32API、中断调用、硬件操作或与操作系统相关的API。
允许使用STL类库,但不能使用MFC或ATL等非ANSI c++标准的类库。例如,不能使用CString类型(属于MFC类库)。
概率题。
手工计算概率,思路是用 甲夺冠的事件总数 / 100000,因为比赛的结果是随机的,所以要用到随机函数rand()产生随机数模拟比赛的结果。如果2场比赛甲都胜利了,那么甲夺冠事件总数 num+1,最后用 num / 100000.0 即可。
解答:0.07679
1 #include <iostream>
2 #include <time.h>
3 #include <stdlib.h>
4 using namespace std;
5 bool p[3][10] =
6 {{1,0,0,0,0,0,0,0,0,0}
7 ,{1,1,1,0,0,0,0,0,0,0}
8 ,{1,1,1,1,1,0,0,0,0,0}};
9 int main()
10 {
11 srand(time(NULL));
12 int num = 0;
13 for(int i=1;i<=100000;i++){
14 int t = rand()%3; //第一轮和哪个队比
15 int tt = rand()%10; //获胜
16 if(p[t][tt]){ //第一轮赢了
17 int t2 = rand()%3; //第二轮和那个队比
18 while(t==t2)
19 t2 = rand()%3;
20 tt = rand()%10;
21 if(p[t2][tt])
22 num++;
23 }
24 }
25 cout<<num/100000.0<<endl;
26 return 0;
27 }
Freecode : www.cnblogs.com/yym2013