限制Boltzmann机(Restricted Boltzmann Machine)
起源:Boltzmann神经网络

Boltzmann神经网络的结构是由Hopfield递归神经网络改良过来的,Hopfield中引入了统计物理学的能量函数的概念。
即,cost函数由统计物理学的能量函数给出,随着网络的训练,能量函数会逐渐变小。
可视为一动力系统,其能量函数的极小值对应系统的稳定平衡点。
Hinton发明的Boltzmann中乘热打铁,对神经元输出引入了随机概率重构的概念。其想法来自于模拟退火算法:
首先在高温下进行搜索,由于此时各状态出现概率相差不大,系统可以很快进入“热平衡状态”,是一种快速找到系统概率的低能区的“粗搜索”过程。
随着温度逐渐降低,各状态出现概率的差距逐渐被扩大,搜索精度不断提高。最后以一较高置信度达到网络能量函数的全局最小点。
随机重构则是Metropolis抽样提出的,作为模拟退火算法的核心:

也就是说,每次重构,都往Δ能量差减少的方向移动,这是RBM的cost函数设计核心,AutoEncoder也是受此启发。
Part I:RBM的结构与目标
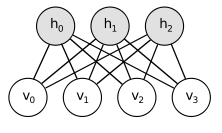
RBM简化了Boltzmann网络,取消了每层神经元之间的连接,即不再是一个递归神经网络,更像是一个MLP。
定义联合能量函数: E(v,h)=−b′v−c′h−h′Wv (b'、c'分别显隐bias做矩阵乘法,h'则是h的全部取值,RBM限定了取值范围{0,1},由激活函数依据概率分布生成)
由此得到v的边缘概率分布:P(v)=∑he−E(v,h)ZZ=∑v∑he−E(v,h)
Z是归一化常数,说白了就是保证概率在[0,1]之间凑出的式子,计算cost函数时可以无视。
RBM的目的是算出尽量符合v(即输入)的概率分布P(v),即实现 argmaxW∏vϵVP(v)
但是问题在于没有标签,没有误差,无法训练W,所以无法训练出P(v)的概率分布。
所以早期的RBM采用从h重构v'来计算误差。重构v',说的好像挺简单,但是需要知道P(v,h)的联合概率分布,用这概率分布去生成v'。
通常情况下,联合概率分布无法计算,但是可以通过条件概率分布+迭代法近似模拟出符合联合概率的样本。
RBM中采用的是Gibbs采样来重构,是MCMC(Monte Carlo Markov Chain)的一种算法特例。
Monte Carlo是根据概率随机生成数据的算法统称,Markov Chain则是符合马尔可夫链的算法统称。【参考】
这样,只要通过又臭又长的马尔可夫链,使用Gibbs采样重构出新样本v'就好了。
有cost函数:cost=argmaxW∑vϵVlogP(v)−argmaxW∑v′ϵV′logP(v′)
这个cost函数在实际计算时候简直是折磨,原因有二: ①Z毫无意义且计算麻烦 ② logP(v)牵扯到E(v,h),E(v,h)的计算也麻烦。
所以Bengio在Learning deep architectures for AI一文中提出了简化的cost函数——FreeEnergy(自由能量)函数。
定义自由能量函数(无视Z+负对数似然):
FreeEnergy(v)=−log(P(v)⋅Z)=−log∑he−E(v,h)
重定义E函数:Energy(v)=−b′v−∑i∑hihi(W⋅v+c),hiϵ{0,1}
这里的精简比较神奇,c′h被刻意X掉了,论文里假设是h只有一个神经元,这样可有可无。c的梯度可以在后半部分求出,所以无须担心c无法更新。
尽管此时的cost函数已经崩坏(Z因子,c'项都不见了),但是骨子还在,对于Gradient Descent影响不大。
这样,参数对称的两部分,可以得到简化P(v) 【推导详见论文】:P(v)=eb′vZ∏i∑hiehi(W⋅v+c)
于是有更加简化的自由能量函数:FreeEnergy(v)=−b′v−∑ilog∑hiehi(W⋅v+c),hiϵ{0,1}
由于取值非0即1,再次简化, FreeEnergy(v)=−b′v−∑ilog(1+e(W⋅v+c))
最终,使用FreeEnergy(v)替代logP(v),有简化cost函数:cost=FreeEnergy(v))−FreeEnergy(v′)
Part II:重构与Gibbs采样
由于V层和H层,每层内各个神经元之间并无连接,因而这些神经元的概率分布是独立的,那么就可以加权通过激活函数计算单个结点的激活概率。
P(hj=1|v)=Sigmoid(Wj⋅v+cj)P(vi=1|h)=Sigmoid(WTi⋅h+bi)
注意反向重构时,同AutoEncoder一样,仍然使用Tied Weight。
这样,就有了条件概率分布,可以构建马尔可夫链了。
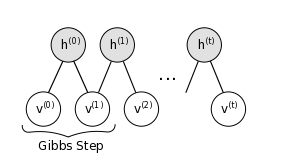
上图是一条波动的链,v0->h0普通的正向传播,忽略不计。
从h0,正式开始Gibbs采样,一个step过程为,hn->vn+1->hn+1,即hvh过程。
vn+1=Bernoulli−Sigmoid(WT⋅hn+b)hn+1=Bernoulli−Sigmoid(W⋅vn+1+c)
当t→∞时,有vt≈v′
Part III K步对比散度算法(CD-K)、可持久化对比散度算法(Persistent CD)
仔细想想RBM中的循环
①外循环:主迭代,训练W,近似逼近P(v|h)、P(h|v)。
②内循环,Gibbs采样,近似逼近P(v)
二重压力下,RBM网络的计算量实在可怕。
Hinton在2002年的 Training Products of Experts by Minimizing Contrastive Divergence 一文中有这个式子:
−∂∂Wij(Q0||Q∞−Q1||Q∞)≈<si,sj>Q0−<si,sj>Q1
即在求v、v'对比相差的cost函数的梯度,用以更新参数时,无限步Gibbs采样的效果与单步Gibbs采样效果差距不大。
数学上很难给出解释,疑似是Gradient Descent与Gibbs Sampling(Gibbs可以看作是GD的先行?)的迭代效果重合。通常取K=1或K=10(更精确)来减少计算量。
既然Gibbs Sampling可以看作是Gradient Descent的先行使者,那么每次做梯度法时候,不必重启马尔可夫链。
而是利用旧链尾产生的hk,作为新链头h0。
数学上仍然很难给出解释,直觉上说,Gradient Descent的小量更新并不会影响马尔可夫链继续扩展,即便狗尾续貂,效果仍然不错。
通过测试,可持久化CD在每次链长较长时效果比较好(k=15),若k=1,则影响较大,不建议使用,选择大量梯度比较稳妥。
Part IV 代理似然函数(Proxies to Likelihood)
Bengio的FreeEnerey方法一定程度上减轻了梯度法的计算量,但是为迭代收敛的评估带来巨大麻烦。
由于归一化因子Z的省略,若使用FreeEnerey的cost函数做评估,那么不同数据集的收敛值几乎是千奇百怪的。
所以需要建立一套数据集公用评估标准,即引入代理似然函数。
代理一:交错熵(or 最小二乘法)
AutoEncoder中使用的cost函数的修改版,Z变成了马尔可夫链尾的h。
cost=v⋅log(Sigmoid(W⋅h−1+b))+(1−v)⋅log(1−Sigmoid(W⋅h−1+b))
代理二:伪造似然函数(Pseudo likelihood)
仔细回想一下可持久化CD,马尔可夫链狗尾续貂,彻夜未眠。
这样,若一直使用链尾的h做交错熵,那么这个交错熵势必是不停波动的,并不很直观的。
因而,引入了伪造似然函数:每次选择v的某一维度值,取反,伪造成重构的v'。
有对数似然函数:PL(x)=∑ilogP(xi|x−i)
当然并没有必要那么精确,每次只需随机抽一个维度进行伪造,乘上N倍即可:
PL(x)=N⋅logP(xi|x−i)i∼Random(0,N)
logP(xi|x−i)的条件概率计算颇为麻烦,利用条件概率公式+贝叶斯假设:
logP(xi|x−i)≈logP(xi)P(xi)+P(x−i)=loge−FreeEnergy(xi)e−FreeEnergy(xi)+e−FreeEnergy(x−i)≈log(Sigmoid(FreeEnergy(x−i)−FreeEnergy(xi)))
Part V 与AutoEncoder的关系
准确来说,AutoEncoder是RBM的简化衍生物。RBM是一个概率生成模型,而AutoEncoder只是一个普通的模型。
神经网络的本质是训练岀能够模拟输入的W,这样,在测试的时候,遇到近似的输入,W能够做出漂亮的响应。
RBM选择概率,是因为有概率论的公式支持。这样优化网络,能够达到上述目标。
只是原始目标不好优化,Hinton才提出对比训练的方法,即绕了个弯子的选择重构。
能量函数使得W朝更大概率方向优化。但是,正如线性回归有最小二乘法和高斯分布两种解释一样。
其实,W的训练大可不必拘泥于概率,AutoEncoder则绕过了这点,直接选择了加权重构,所以cost函数简单。
可以这么说,重构的数学理论基础就是RBM的原始目标函数。而概率重构启发了直接重构。两者近似等价。
从马尔可夫链上看,AutoEncoder可看作是链长为1的特殊形式,即一次重构,而RBM是多次重构。
能使用直接重构的另一个原因是,Hinton在实验中发现,梯度法的一次重构效果出奇好。
所以AutoEncoder中摒弃了麻烦的Gibbs采样过程。
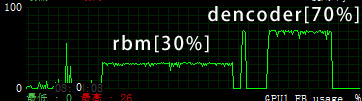
从GPU计算来看,k=1情况下,AutoEncoer的GPU利用率高(70%),RBM利用率低(30%),一开始实现的时候吓了一跳。
CUDA执行马尔可夫链效率并不高,目测二项分布随机重构是由CPU执行的( _(:_」∠)_想想好像GPU没那么高级 )
尤其在把batch_size设为600之后,RBM的GPU利用率居然只有(10%), 所以官方教程把batch_size设为了20,来减小概率生成的计算压力。
当然k=15时,GPU加速之后仍然十分缓慢。RBM不愧是硬件杀手。
(本图来自MSI Afterburner,GTX 765M,OC(847/2512/913))
Part VI Gaussian-Bernoulli RBM
仔细看看Bernoulli-Bernoulli的重构过程:
[0/1]->[0/1]->[0/1].....,由于二项分布是离散概率分布,所以重构生成值要么是0,要么是1,似乎有些不靠谱。
所以,就有了Gaussian-Bernoulli RBM,在v层中强制引入连续数值型Gaussian噪声,主要对原RBM做以下修改:
E(v,h)=∑i(vi−bi)22σi2−c′h−h′WvσP(vi=v|h)=N(bi+σi(W⋅h),σ2i)P(hi=1|v)=Sigmoid(W⋅vσ+c)
其中Size(σ)=NVisble,为正态分布标准差,为正值,一般不作训练,取定值1,原因有二:
其一:梯度法训练会产生负值和0,导致训练失败
其二:Gaussian过程并不需要精确的范围,取的只是正态分布的连续特征,提供Gaussian噪声。
当然,还是有人提出了可训练σ的改进方法,个人实际测试并没有成功,σ在梯度下降过程中,出现了过大数值问题,导致网络崩溃。参考
Gaussian过程极易产生误解,由于正态分布的取值范围是R,所以对比散度样本不可以再使用由Gaussian分布生成v’
Gaussian过程主要为从二项[0/1]的h,提供一个连续型重构缓冲范围,而不仅仅把马尔可夫链的运行局限在0/1之间
这样做的原因是,一般输入是连续型值,符合的是0~1之间的连续概率分布,而不是简单的离散二项分布。
然后再把Gaussian分布映射回Bernoulli分布h',最后使用的是h[-1],令:v′=Bernoulli−Sigmoid(W⋅h[−1]+b)
对比图如下:


左图(Bernoulli-Bernoulli) 右图(Gaussian-Bernoulli)
可以看到,Gaussian分布使得参数学习到了更多的特征,但是也带来了更大的重构误差,以及更快下降到局部最小值。学习率和Bernoulli-Bernoulli相同情况下,epoch2就过拟合了。
Hinton在 A practical guide to training restricted Boltzmann machines 提到,Gaussian-Bernoulli模型不稳定,由于Gaussian分布的上界不定,
所以,学习率较之于Bernoulli-Bernoulli应该下降1~2个数量级。同时,应当慎用CD-10、Persistent CD,这些会带来更不稳定的重构。(个人测试情况,似然几乎无法下降)