(mathsf{9.2})
(mathcal{During})
T1 sb题，上来因式分解反手就秒，火速拍上
T2 第一眼数学题，写了暴力找规律，找到考试结束（误
T3 题目看了，觉得这题很生硬，完全就不会写呢
最后 T2 暴力没模，只有 10 分。
(mathcal{After})
T1
不说了
#include <bits/stdc++.h>
const int N = 1e5 + 10;
int T, n, pr[N], v[N], len = 0;
void Pre()
{
v[1] = 1;
for (int i = 2; i <= N - 10; ++i) {
if (!v[i]) pr[++len] = i;
for (int j = 1; j <= len && pr[j] * i <= N - 10; ++j) {
v[pr[j] * i] = pr[j];
if (i % pr[j] == 0) break;
}
}
}
int main(void)
{
freopen("pair.in", "r", stdin), freopen("pair.out", "w", stdout);
Pre(), scanf("%d", &T);
while (T--) {
scanf("%d", &n), ++n;
int num, sum = 1, y = n;
for (int i = 1; pr[i] * pr[i] <= n; ++i)
if (y % pr[i] == 0) {
num = 0;
while (y % pr[i] == 0) ++num, y /= pr[i];
sum *= num + 1;
}
if (y > 1) sum <<= 1;
printf("%d
", sum);
}
return 0;
}
T2
考虑 DP。设 (f_{i,j}) 为前 i 个位置，存在 j 对相邻顺序对时的方案数
对于第 i + 1 个位置，我们可以插入的位置总共有 i + 1 个。
- 在其中 j 个位置插入i + 1， 不会使相邻顺序对数增加，因为数列长这样：
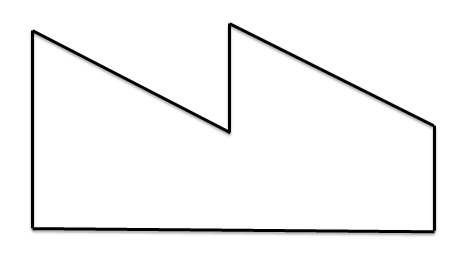
在“峰”前加入一个目前最大的 i + 1，显然顺序对数不会改变。
这样的“山峰”总共有 j + 1 个。
- 反之，在任意递减子序列中插入i + 1，都将使顺序对数 + 1，可插入位置有 (i + 1) - (j + 1) = i - j 个。
因此，我们有 (i - j) 个位置贡献为 (f_{i - 1, j - 1})， 有 (j + 1) 个位置贡献为 (f_{i - 1, j})。故：
[f_{i,j} = (i - j) imes f_{i - 1, j - 1} +(j +1) imes f_{i - 1, j}
]
初值： 任意 (f_{i, i - 1}=1,f_{i,0}=1)，显而易见。
(mathbf{Code:})
#include <bits/stdc++.h>
const int N = 1e3 + 10, mod = 2012;
using namespace std;
int n, K, f[N][N];
int main()
{
freopen("permutation.in", "r", stdin), freopen("permutation.out", "w", stdout);
scanf("%d%d", &n, &K);
for (int i = 1; i <= n; ++i) f[i][i - 1] = f[i][0] = 1;
for (int i = 3; i <= n; ++i) for (int j = 1; j < i - 1; ++j)
f[i][j] = (1LL * (i - j) * f[i - 1][j - 1] % mod + 1LL * (j + 1) * f[i - 1][j] % mod) % mod;
printf("%d
", f[n][K]);
return 0;
}
T3
观察性质：
最短路树上最后一条边不能用了，那么必定是通过非树边代替的，那么根据直觉（zld）观察，显然我们至多，也至少使用一条非树边：如果使用多条非树边，用原最短路树上边代替，显然不会劣；而树的不连通使我们不得不使用至少一条边。
有这个性质，我们可以开始考虑每条非树边对答案的影响。
(mathbb{Solution})
我们发现对于 S(1) 和 某点 T(x)，答案 ans 是通过某些非树边 (u, v) 更新而来。由于到 T 的对短路树上往父亲边断裂，那么要使联通，u、v 必然一个在 1 所在连通块，一个在 x 所在连通块（实际上就是 T 的子树内）。
合法的路径为 (distance[S ->u] + weight(u,v) + distance[v->T])，distance 为最短距离，显然就是最短路树上距离，可以快速求出：设 (dis_x) 为根到 x 的距离（非深度），则
[distance(S->u) = dis_u,distance(v->T) = dis_v - dis_T [ t{Point(v) is in Subtree(T)}]
]
故 (mathrm{length} = dis_u + dis_v + W(u,v) - dis_T)，其中由边 (u, v) 决定的只有前三个值，可据此更新所有能影响到的点的最优值，可有数据结构维护（线段树之类的）。
考虑每条边 (u, v) 能更新的点的范围，根据上面加粗条件（分属不同连通块），可知影响范围为两点间路径上除LCA外的所有点，用上面的值更新这些点的最优值即可，最后将由点决定的 (dis_T) 减去即为答案。
(mathbf{Code:})
树剖求树上路径及 LCA。代码已解压 /xyx
/* 解压痕迹明显/xyx */
#include <bits/stdc++.h>
#define swap(x, y) (x ^= y ^= x ^= y)
#define mp(x, y) make_pair(x, y)
const int N = 4e3 + 10, M = 1e5 + 10, inf = INT_MAX;
using namespace std;
int n, m, top[N], dis[N], d[N], si[N], hs[N], Fa[N], tr[N], vs = 0;
struct Graph { int x, y, z, o; } e[M];
struct Tree {
int to[N << 1], net[N << 1], w[N << 1], fl[N], len;
inline void inc(int x, int y, int z) {
return to[++len] = y, net[len] = fl[x], w[len] = z, fl[x] = len, void();
}
} T;
class Point { public: int minn, la; };
struct Segmentree {
Point t[N << 2];
#define m(p) t[p].minn
#define ls (p << 1)
#define rs (ls | 1)
#define mid ((x + y) >> 1)
#define Ls ls, x, mid
#define Rs rs, mid + 1, y
inline void Push(int p) { return m(p) = min(m(ls), m(rs)), void(); }
inline void kk(int &a, int b) { return a = min(a, b), void(); }
void Build(int p, int x, int y) {
m(p) = t[p].la = inf;
return x == y ? void() : (Build(Ls), Build(Rs));
}
inline void Update(int p, int lson, int rson) {
return t[p].la >= inf
? void()
: (kk(m(ls), t[p].la), kk(m(rs), t[p].la), kk(t[ls].la, t[p].la),
kk(t[rs].la, t[p].la), t[p].la = inf, void());
}
inline void Modify(int p, int x, int y, int l, int r, int v) {
if (l > r || x > y || l > y || x > r) return void();
return l <= x && y <= r
? (kk(m(p), v), kk(t[p].la, v), void())
: (Update(p, mid - x + 1, y - mid), Modify(Ls, l, r, v), Modify(Rs, l, r, v), void());
}
inline int Ask(int p, int x, int y, int pos) {
if (x == y) return m(p);
Update(p, mid - x + 1, y - mid); return pos <= mid ? Ask(Ls, pos) : Ask(Rs, pos);
}
#undef ls
#undef rs
} Se;
inline int read() {
int s = 0; char c = getchar(); for (; !isdigit(c); c = getchar());
for (; isdigit(c); c = getchar()) s = (s << 3) + (s << 1) + c - 48; return s;
}
template <class T>
inline void write(T x) {
(x < 0 ? x = ~x + 1, putchar('-') : 0), (x > 9 ? write(x / 10) : void());
return putchar(x % 10 + 48), void();
}
void Dfs(int u, int fa) {
d[u] = d[fa] + 1, Fa[u] = fa, si[u] = 1;
for (int i = T.fl[u]; i; i = T.net[i]) {
int v = T.to[i]; if (v == fa) continue;
dis[v] = dis[u] + T.w[i],
Dfs(v, u),
si[u] += si[v], (si[hs[u]] < si[v] ? hs[u] = v : 0);
}
}
void Dfs_chain(int u, int k) {
top[tr[u] = ++vs, u] = k;
if (!hs[u]) return void();
Dfs_chain(hs[u], k);
for (int i = T.fl[u]; i; i = T.net[i]) {
int v = T.to[i]; if (v == hs[u] || v == Fa[u]) continue;
Dfs_chain(v, v);
}
}
inline int Lca(int x, int y) {
while (top[x] ^ top[y]) (d[top[x]] < d[top[y]] ? swap(x, y) : 0), x = Fa[top[x]];
return d[x] < d[y] ? x : y;
}
inline int Get_la(int x, int y) {
while (top[x] ^ top[y]) {
(d[top[x]] < d[top[y]] ? swap(x, y) : 0);
if (Fa[top[x]] == y) return top[x];
x = Fa[top[x]];
}
return hs[(d[x] < d[y] ? x : y)];
}
inline void Modify(int x, int y, int z) {
while (top[x] ^ top[y]) (d[top[x]] < d[top[y]] ? swap(x, y) : 0),
Se.Modify(1, 1, n, tr[top[x]], tr[x], z), x = Fa[top[x]];
if (d[x] < d[y]) swap(x, y); return Se.Modify(1, 1, n, tr[y], tr[x], z);
}
int main(void) {
freopen("shortest.in", "r", stdin), freopen("shortest.out", "w", stdout);
n = read(), m = read();
for (int i = 1; i <= m; ++i) {
int x = read(), y = read(), z = read(), o = read();
e[i] = (Graph) {x, y, z, o };
if (o == 1) T.inc(x, y, z), T.inc(y, x, z);
}
Dfs(1, 0), Dfs_chain(1, 1), Se.Build(1, 1, n);
for (int i = 1; i <= m; ++i) if (!e[i].o) {
int u = e[i].x, v = e[i].y, w = e[i].z + dis[u] + dis[v];
int LCA = Lca(u, v), ls = Get_la(u, LCA), rs = Get_la(v, LCA);
if (u != LCA) Modify(ls, u, w);
if (v != LCA) Modify(rs, v, w);
}
for (int i = 2; i <= n; ++i)
vs = Se.Ask(1, 1, n, tr[i]) - dis[i],
write(vs >= inf / 2 ? -1 : vs), i < n ? putchar(32) : 0;
return 0;
}