后缀数组

哇！终于学习了后缀数组，现在逮着时间来总结归纳一下，免得过久了就什么都记不到了。

这篇博客真的写的很详细，可以看一下。

我们要先知道后缀数组可以做什么，后缀数组自然是与一个字符串的后缀有关，在处理字符串子串的问题中能起很大的作用。

为什么可以处理子串呢?这里有一个很重要的认识：子串是某个后缀的前缀。

后缀数组的思想

（摘自学长的PPT）后缀数组其实本身是简单的，就是要把字符串 S 的所有后缀按照字典序排序，然后利用排好序之后的性质处理问题。

好，那怎么排序呢？

sort并且比较函数中暴力比较 ？  O(n^2log)
快排(nlogn)每个后缀，但是这是字符串，所以比较任意两个后缀的复杂度其实是O(n)，这样一来就是接近O(n^2 logn)的复杂度

sort并且比较函数中hash二分？ O(n log^2)

然而后缀数组更快。

这里用了倍增的思想，以下举例说明。

比如一个字符串S：aabaa

它的后缀分别是：aabaa，abaa，baa，aa，a

显然我们用肉眼观察出，最后后缀排好序后应该是：a，aa，aabaa，abaa，baa。

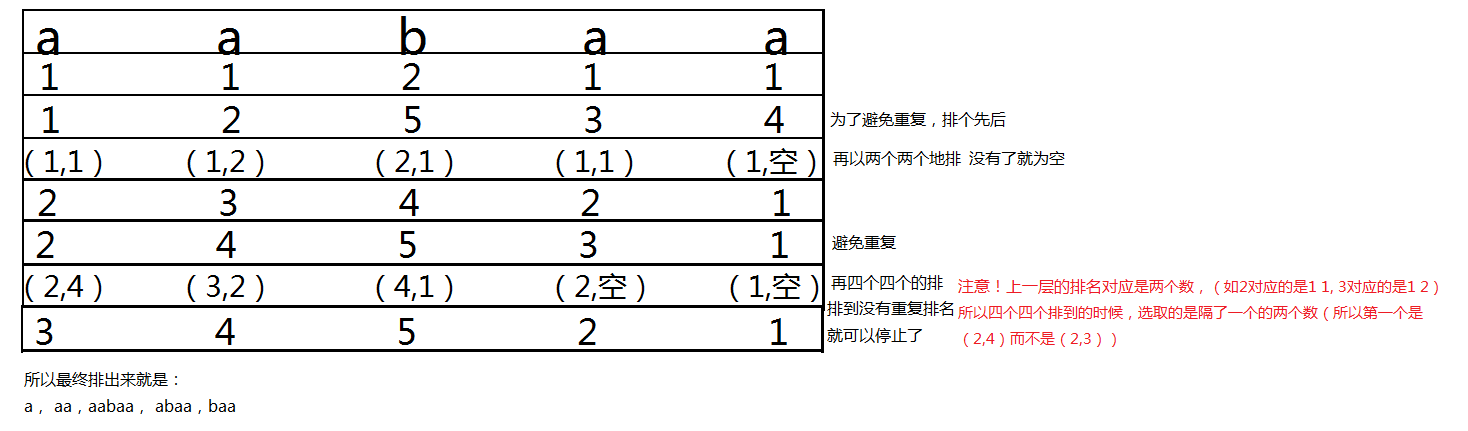
倍增就体现在先以一个字母排，再以两个字母排，然后是4个......2^n个

---

然后，让我们明白两个数组的定义（这个很重要）：

SA[i]表示排名为i的后缀的起始位置的下标

rk[i]表示起始位置的下标为i的后缀的排名

我们也可以这么理解：SA表示排名为i的后缀是什么，rk表示第i个后缀的排名是什么。

而且，SA和rk显然是成一个相反关系的。rk[SA[i]]=i

---

 我们用基数排序实现，开一个值域数组。

如 3 3 2 1

它的值域数组就开0到3

对应的个数分别是0 1 1 2

求一个前缀，就是0 1 2 4 ，（就是从cnt数组）可以理解为一开始以单字母排序在序列中它作为后缀的开端，后缀的排名（是不是感觉和SA有一点点瓜系）

注意！求SA时cnt从后往前for，保证后缀的排名互异。（具体看代码吧）

这里还要提出两个概念：第一关键字和第二关键字（也就是上面图中括号里的左右的值）。

如果是第一步以单个字母排序时，就是单关键字排序

aabaa 以1表示a，2表示b

值域数组下标        1 2

个数                      4 1

求一个前缀和        4 5

那么存在cnt里的就应该是  4 4 5 4 4

但我们要求排名不重复，就通过一点小处理，变成了1 2 5 3 4

我们可以先看一下单关键字排序的代码

for(int i=0;i<=up;++i) cnt[i]=0;
for(i=1;i<=len;++i) cnt[fri[i]]++;
for(i=1;i<=up;++i) cnt[i]+=cnt[i-1];
for(int i=len;i>=1;--i) SA[cnt[fri[i]]--]=i; //使得排名互异，且前面的排名更小

假设排完序之后先放入SA数组，SA[i] 表示排名为 i 的后缀的起始位置，fir[i]表示第 i 个后缀的第一关键字的值

up就是第二关键字的个数，因为（第二关键字会少于第一关键字，出现了为空的情况，所以要保存一下）

然后我们看一下双关键字排序（其实只有第一次是单关键字，后面都是双关键字）

先贴出代码

int zj=0;
for(int i=len-k+1;i<=len;++i) sec[++zj]=i;
for(int i=1;i<len-k+1;++i) sec[++zj]=SA[i]-k;
for(int i=1;i<=up;++i) cnt[i]=0;
for(i=1;i<=len;++i) cnt[fri[sec[i]]]++;
for(i=1;i<=up;++i) cnt[i]+=cnt[i-1];  
for(int i=len;i>=1;--i) SA[cnt[fri[sec[i]]]--]=sec[i];

在双关键字排序中，以第二关键字从小到大的顺序作为下标进行第一关键字的排序即可。此处 sec[i] 表示第二关键字排名为 i 的后缀起始位置

k就是以k个字母进行排序（也就是1,2,4,8......）

如果此时len-i的长度小于了k，那么第二关键字肯定为空

不然就是后面的某个第一关键字作为第二关键字

---

感觉有点糊其实好像我也不是理解地很透彻看一下这篇博客

最后是get_SA的总的代码

int up=len;
void get_SA()
{
    for(int i=0;i<=up;++i) cnt[i]=0;
    for(i=1;i<=len;++i) cnt[fri[i]]++;
    for(i=1;i<=up;++i) cnt[i]+=cnt[i-1];
    for(int i=len;i>=1;--i) SA[cnt[fri[i]]--]=i; 
    int k=1;
    while(k<len)
    {
        int zj=0;
        for(int i=len-k+1;i<=len;++i) sec[++zj]=i;
        for(int i=1;i<len-k+1;++i) sec[++zj]=SA[i]-k;
        for(int i=1;i<=up;++i) cnt[i]=0;
        for(i=1;i<=len;++i) cnt[fri[sec[i]]]++;
        for(i=1;i<=up;++i) cnt[i]+=cnt[i-1];  
        for(int i=len;i>=1;--i) SA[cnt[fri[sec[i]]]--]=sec[i];
        swap(fir,tmp);
        zj=0;fri[SA[1]]=++zj;
        for(int i=2;i<=len;++i)
        {
            if(SA[i]+k<=len&&SA[i-1]+k<=len&&tmp[SA[i]]==tmp[SA[i-1]]&&tmp[SA[i]+k]==tmp[SA[i-1]+k])
              fri[SA[i]]=zj;//如果现在的这名和前一名的两个关键字相等就是并列，否则就排到后一名
            else fri[SA[i]]=++zj;
        }
        if(zj==len) break;
        up=zj;
        k=k*2;
    }
}

---

然后呢，还要再介绍一个东西才可以做题

height数组：SA[i]和SA[i-1]的LCP长度（LCP即最长公共前缀）

那么有了后缀的前缀就可以处理子串了

void get_h()
{
    int ht=0;
    for(int i=1;i<=len;++i) rank[SA[i]]=i;
    for(int i=1;i<=len;++i)
    {
        int t=SA[rank[i]-1];
        while(t+ht<=len&&i+ht<=len&&s[t+ht]==s[i+ht]) ht++;//一定要注意一下范围 
        h[rank[i]]=ht;
        ht=max(0,ht-1);
    }
}