[Violet]樱花（数学推导+n！质因子分解）

传送门

以下图片公式推导摘自洛谷题解

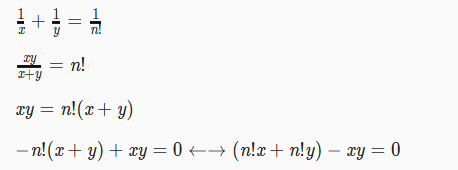
然后我觉得这道题就价值在如何求阶乘的因子个数。

实现的时候每次除一个p，就是从从p^k的倍数的个数变为求p^(k+1)的倍数的个数了。

最后统计答案时乘num*2+1，因为求的是（n!）^2的因子。

#include<bits/stdc++.h>
#define LL long long
#define re register
#define INF 2100000000
#define N 1000013
#define mod 1000000007
using namespace std;
LL read()
{
    LL x=0,f=1;char s=getchar();
    while(s<'0'||s>'9'){if(s=='-')f=-1;s=getchar();}
    while(s>='0'&&s<='9'){x=x*10+s-'0';s=getchar();}
    return x*f;
}
int notp[N],prime[N];
int tot=0;
void init()
{
    for(int i=2;i<=N;++i)
    {
        if(!notp[i])prime[++tot]=i;
        for(int j=1;j<=tot&&i*prime[j]<=N;++j)
        {
            notp[i*prime[j]]=1;
            if(i%prime[j]==0)break;
        }
    }
}
int main()
{
    LL n=read();
    init();
    LL ans=1;
    for(int i=1;i<=tot;++i)
    {
        LL res=0;
        for(int j=n;j;j/=prime[i])res+=j/prime[i];
        ans=(ans*(res*2+1)%mod)%mod;
    }
    printf("%lld
",ans);
}