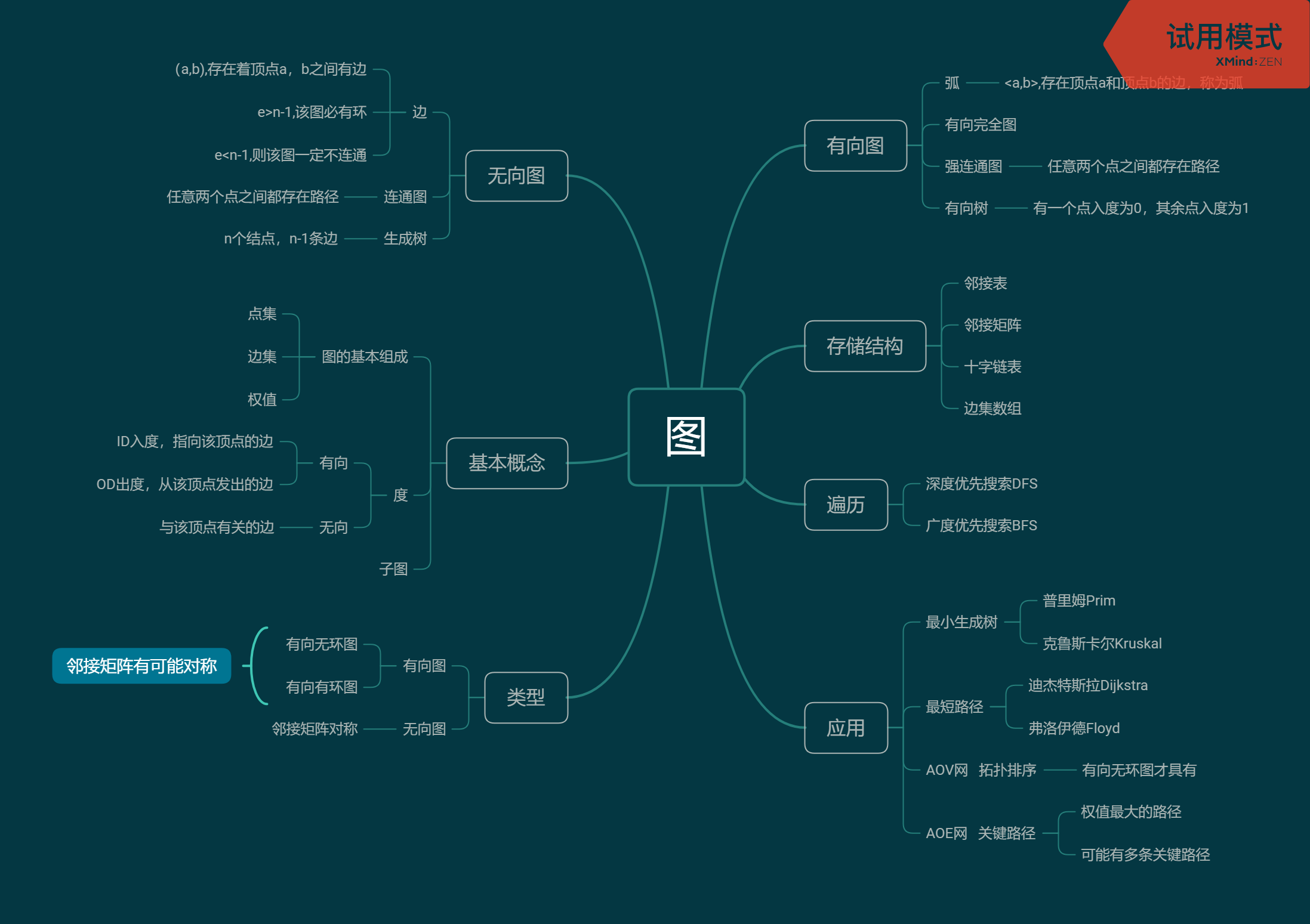
思维导图:
基本概念:
图(graph):图是由顶点的有穷非空集合和顶点之间边的集合组成,通常表示为:G(V,E),其中,G表示一个图,V是图G中的顶点的集合,E是图G中边的集合。
顶点(Vertex):图中的数据元素。线性表中我们把数据元素叫元素,树中将数据元素叫结点。
边:顶点之间的逻辑关系用边来表示,边集可以是空的。
无向边(Edge):若顶点V1到V2之间的边没有方向,则称这条边为无向边。
无向图(Undirected graphs):图中任意两个顶点之间的边都是无向边。(A,D)=(D,A)
有向边:若从顶点V1到V2的边有方向,则称这条边为有向边,也称弧(Arc)。用<V1,V2>表示,V1为狐尾(Tail),V2为弧头(Head)。(V1,V2)≠(V2,V1)。
有向图(Directed graphs):图中任意两个顶点之间的边都是有向边。
注意:无向边用“()”,而有向边用“< >”表示。
简单图:图中不存在顶点到其自身的边,且同一条边不重复出现。
无向完全图:无向图中,任意两个顶点之间都存在边。
有向完全图:有向图中,任意两个顶点之间都存在方向互为相反的两条弧。
稀疏图:有很少条边。
稠密图:有很多条边。
权(Weight):与图的边或弧相关的数。
网(Network):带权的图。
子图(Subgraph):假设G=(V,{E})和G‘=(V',{E'}),如果V'包含于V且E'包含于E,则称G'为G的子图。
度(Degree):无向图中,与顶点V相关联的边的数目。有向图中,入度表示指向自己的边的数目,出度表示指向其他边的数目,该顶点的度等于入度与出度的和。
路径的长度:一条路径上边或弧的数量。
连通图:图中任意两个顶点都是连通的。
连通分量:无向图中的极大连通子图。(子图必须是连通的且含有极大顶点数)。图1有两个连通分量
强连通分量:有向图中的极大强连通子图。
生成树:无向图中连通且n个顶点n-1条边叫生成树。
有向树:有向图中一顶点入度为0其余顶点入度为1。
森林:一个有向图由若干棵有向树构成生成森林。
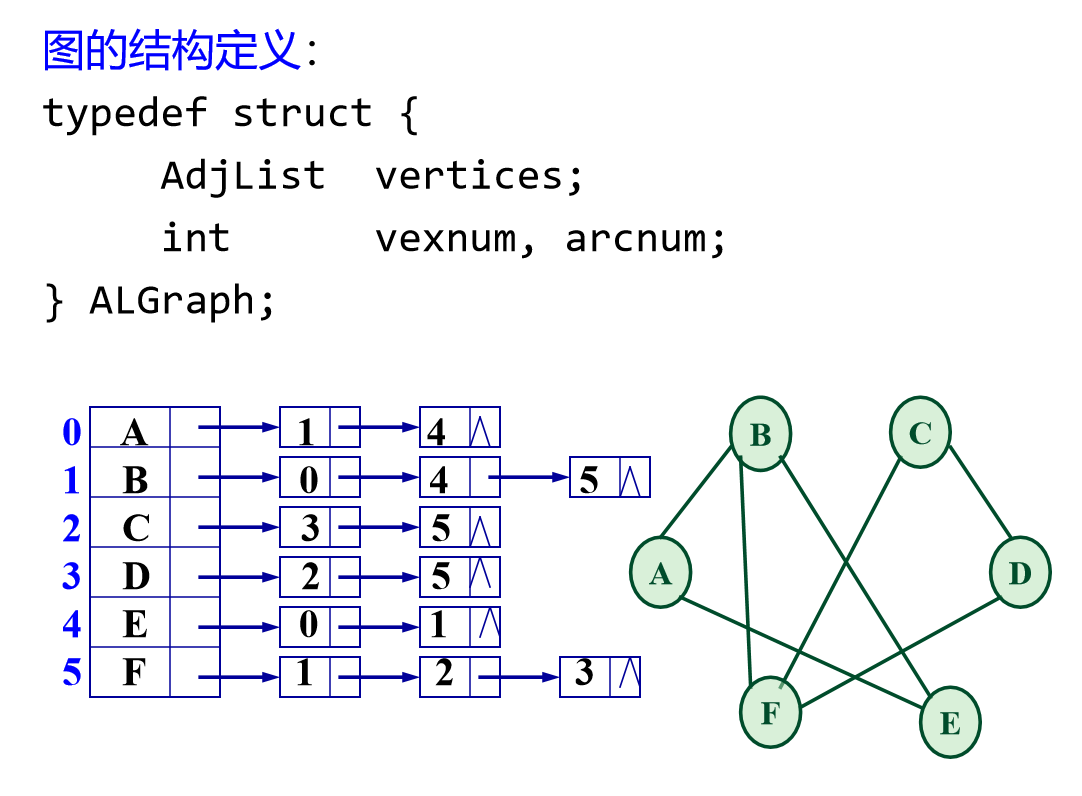
存储结构:
邻接矩阵:

邻接表:
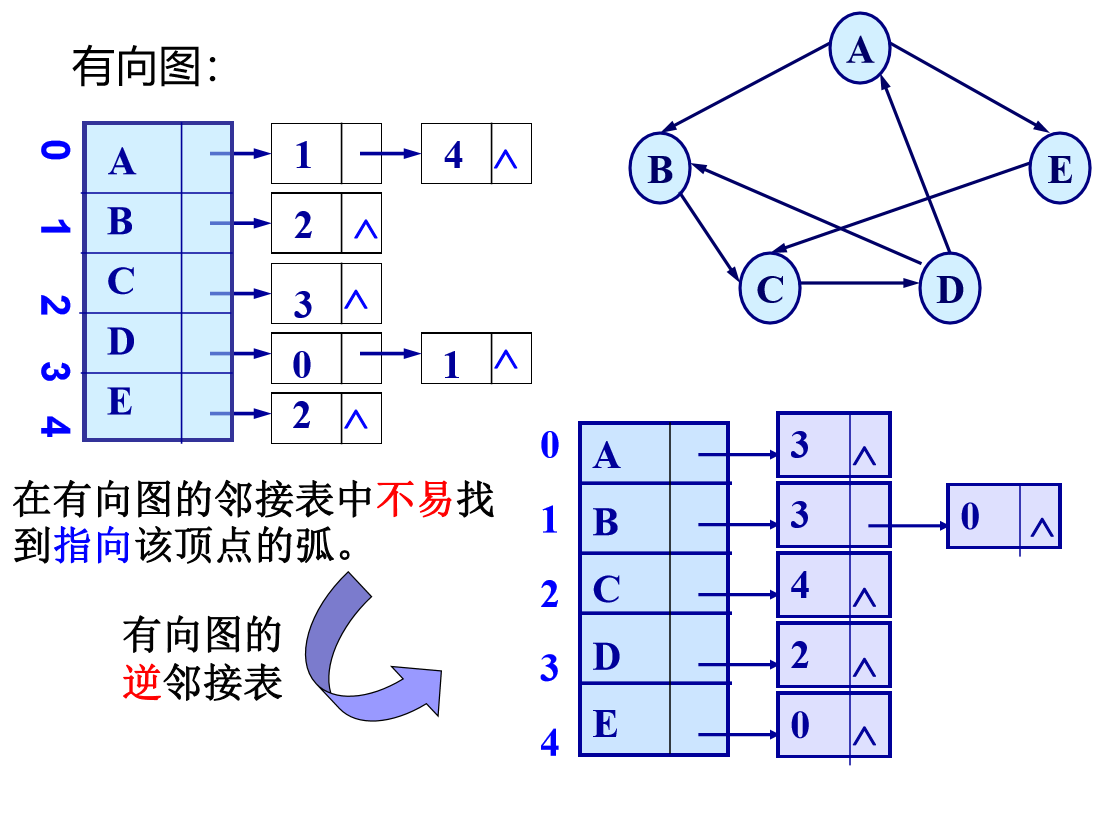
有向图:
图的遍历:
1.深度优先遍历(DFS):
从图中某个顶点v出发,访问此顶点,然后从v的未被访问的邻接点出发深度优先遍历图,直至图中所有和v有路径相通的顶点都被访问到。
举例:

2.广度优先遍历(BFS):
类似于树的层次遍历。
举例:

最小生成树:
生成树:一个连通图的生成树是一个极小的连通子图,它含有图中全部的顶点,但只有足以构成一棵树的n-1条边。
最小(代价)生成树:Minimum (cost) spanning tree。构造连通网的最小代价生成树称为最小生成树。(一棵生成树的代价就是树上各边的代价之和)
构造最小生成树的2种算法:Prim算法、Kruskal算法。
Prim算法

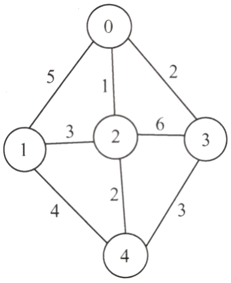
例子:
1)从顶点0开始,此时候选边为5、1、2,从中选择最小边长为1的边,加入到当前树中。
2)此时已有的边:(0,2),此时已有顶点:0、2
此时候选边为5、3、2、6、2,最小边长为2,选择其加入(有2条,随便选1条符合条件即可)
3)此时已有的边:(0,2),(0,3),此时已有顶点:0、2、3
此时候选边为5、3、2、3,最小边长为2,选择其加入
4)此时已有的边:(0,2),(0,3),(2,4),此时已有顶点:0、2、3、4
此时侯选边为5、3、4,最小边长为3,选择其加入
5)此时已有的边:(0,2),(0,3),(2,4),(2,1),此时已有顶点:0、1、2、3、4
已包含全部顶点,生成树求解过程完毕。
Kruskal算法

例子:

两个算法对比:
Prim算法:针对顶点,对于稠密图(边数非常多的情况)更好;
Kruskal算法:针对边,对于稀疏图(边数少)时更好。
最短路径:
基本概念:最短路径是指两顶点之间经过的边上权值之和最少的路径。
求最短路径的算法:Dijkstra算法(从某个源点到其余各顶点的最短路径)、Floyd算法(每一对顶点之间的最短路径)
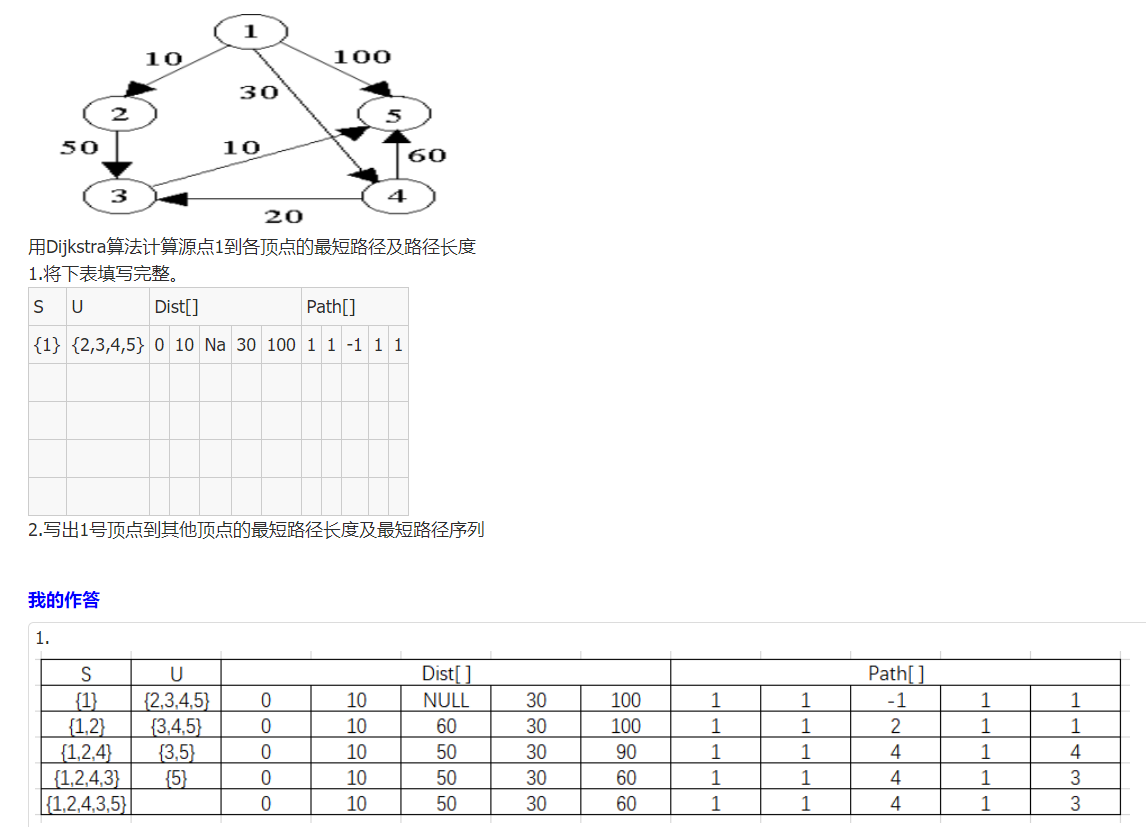
Dijkstra:
思想:从图中选取到源点v0路径长度最短的顶点并入到集合S中,修改顶点v0到剩下的顶点的最短路径长度值,直到所有顶点都并入到S中为止。
例子:
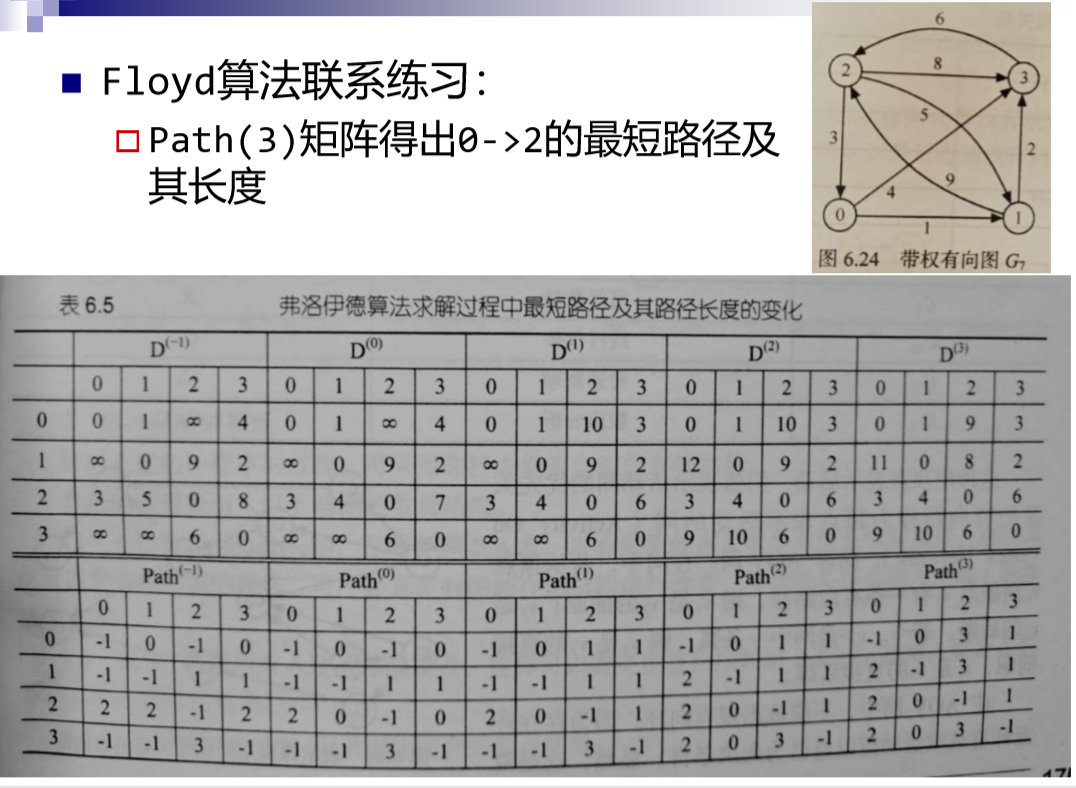
Floyd:
思想:
1.从任意一条单边路径开始。所有两点之间的距离是边的权,如果两点之间没有边相连,则权为无穷大。
2.对于每一对顶点 u 和 v,看看是否存在一个顶点 w 使得从 u 到 w 再到 v 比已知的路径更短。如果是更新它。
例子:
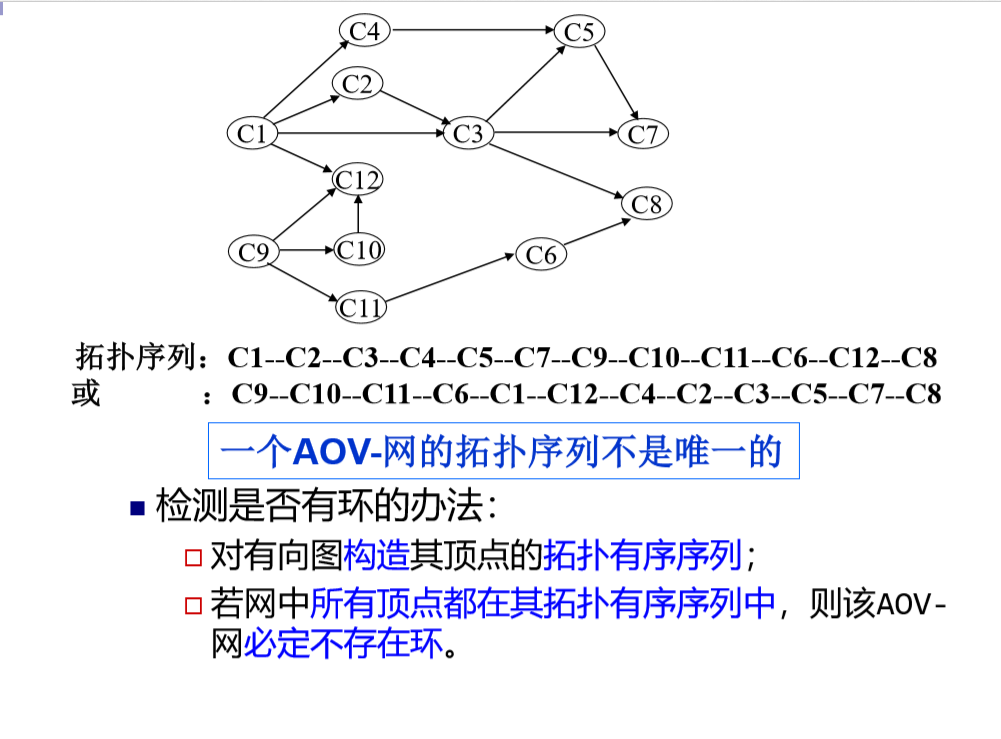
拓扑排序:
AOV网:重点是顶点。顶点表示活动,边表示活动之间的先后关系。
拓扑排序:
基本概念:拓扑排序是对有向无环图G的排序,是将G中所有顶点排成一个线性序列,使得图中任意一对顶点u和v,若存在u到v的路径,则在拓扑排序序列中一定是u出现在v的前边。(与边无关)
实现思路:从有向无环图中选择一个入度为0的顶点输出,然后删去此顶点,并删除以此顶点为尾的弧,继续重复此步骤,直到输出全部顶点或者AOV网中不存在入度为0的顶点为止。
例子:
AOE网:重点是边。边表示活动,顶点表示事件(事件是新活动开始或旧活动结束的标志)
关键路径:
基本概念:在AOE(边表示活动)网中,从源点到汇点的所有路径中,具有最大路径长度的路径称为关键路径。把关键路径上的活动称为关键活动。关键路径既是最短,又是最长。
最短:完成工期的最短事件。
最长:图中的最长路径。
求关键路径的过程:
Step1.对事件(顶点)进行拓扑排序:(比较复杂繁琐的一步)
Step1.1求事件的最早发生时间(从前往后计算)(上一个事件+权值)的最大值(多对1,求最大值)
Step1.2求事件的最晚发生时间(从后往前计算)(下一个事件-权值)的最小值(1对多,求最小值)
Step2:写出活动(边):(该步骤完全根据Step1中的写,不复杂)
Step2.1:求活动的最早发生时间(即上一个事件的最早开始时间)
Step2.2:求活动的最晚发生时间(即下一个事件的最晚开始时间-边的权值)
求最早:从前往后计算
求最晚:从后往前计算
疑难点:
迪杰特斯拉算法:
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
const int MAXV = 201;
const int INF = 0x3fffffff;
//邻接矩阵版本
int n, m, s;
int G[MAXV][MAXV];
int d[MAXV]; //各个点到出发点的最短路径
bool Vis[MAXV] = { false };
//并查集输出最短路径
int f[MAXV];
void Dijkstra(int s) { //起始点
fill(d, d + MAXV, INF);
d[s] = 0; //不管什么情况一定要初始化
for (int i = 0; i < n; ++i) {
//寻找最小的点
int u = -1, MIN = INF;
for (int j = 0; j < n; ++j) {
if (!Vis[j] && d[j] < MIN) {
MIN = d[j];
u = j;
}
}
if (u == -1) return; //所有边访问完成,算法完成,退出
//更新每个结点的最小距离
Vis[u] = true; //设置本结点为访问结点
for (int v = 0; v < n; ++v) {
if (!Vis[v] && G[u][v] != INF && G[u][v] + d[u] < d[v]) {
d[v] = G[u][v] + d[u]; //优化结点
f[v] = u; //并查集
}
}
}
}
void getRoute(int e) { //如果要求路径的话,可以用并查集实现
cout << e;
if (f[e] != e) {
cout << " ";
getRoute(f[e]);
}
}
int main() {
fill(G[0], G[0] + MAXV * MAXV, INF); //切记一定要赋初值
int u, v, w;
for (int i = 0; i < MAXV; ++i) {
f[i] = i; //并查集更新
}
scanf("%d %d %d", &n, &m, &s);
for (int i = 0; i < m; ++i) {
scanf("%d %d %d", &u, &v, &w);
G[u][v] = w;
}
Dijkstra(s); //起始点
for (int i = 0; i < n; ++i) {
printf("%d
", d[i]);
getRoute(i);
cout << endl;
}
system("PAUSE");
return 0;
}