在了解空洞卷积时候发现了Kronecker convolution是对空洞卷积的改进,于是学习了一下 ,原文连接:1812.04945v1.pdf (arxiv.org) 个人理解如下:
首先,对于一个普通卷积,假设输入为A,A的大小为(Ha,Wa,Ca),卷积后的输出为B,B的大小为(Hb,Wb,Cb),卷积核 K 的大小为Cb*Ca*(2k+1)(2k+1)。
对于所提出的Kronecker卷积,引入了一个变换矩阵 F ,通过F与K的乘积来扩展K,K经过扩展后记为K‘,K‘的大小为r1(2k+1)*r1(2k+1)。相应地,A中参与卷积的Patch大小也就从原来的(2k+1)(2k+1)变成了(2k+1)r1*(2k+1)r1。其中F由单位矩阵和0矩阵组成,大小为r1*r1,r1被称为内部膨胀因子,用来控制卷积核的膨胀率。r2为内部共享因子,控制子区域的大小。
也就是说 与单纯插入0的空洞卷积相比,Kronecker卷积通过与变换矩阵F的乘积展开核,内部膨胀因子控制核的膨胀率,内部共享因子控制子区域的大小。
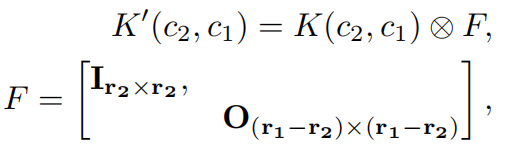
那么为什么F与K相乘后K的大小增大了呢?
这是因为F与K的相乘方法为 Kronecker product ,即克罗内克积,其定义如下:
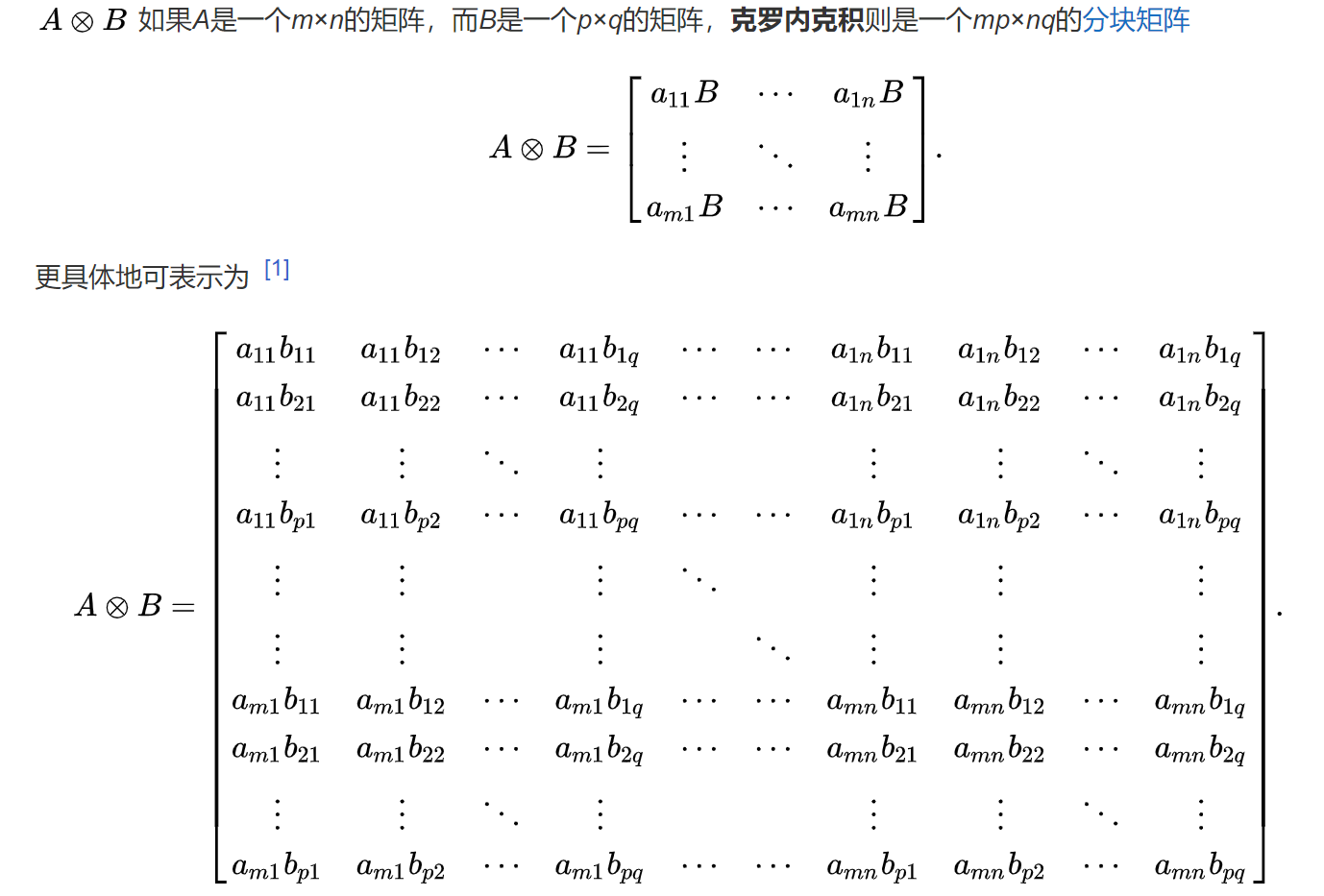
所以我的理解是 卷积仍然是普通的卷积,但是卷积核发生了变化,卷积核的变化过程中采用了克罗内克积。