【题解】Luogu P5288 [HNOI2019]多边形

原题传送门

HN的题目就是毒瘤

我们有以下猜想：

1.最后所有的线都连到了n号点上

2.最小步数应该为n-3-已经连到n号点的线段数量

本来有些边((a_i,n))会将整个图分割成很多个区间。对于一个区间([l,r])，(l,r)之间必定存在一条边，并且一定存在点(mid)有((mid,l),mid(mid,r))的边，所以我们珂以用一次旋转使得((l,r))变成((mid,n))，这样这个区间有珂以分成两个子区间，珂以建出二叉树。一直如此，直到(r=l+1)为止。我们现在就要考虑如何计算方案数，父节点的旋转一定在子节点的旋转之前，但子节点间互不干扰，所以就是一个插入排序方案数的问题，明显两个子树顺序影响就是把答案乘上(frac{(size(ls)+size(rs))!}{size(ls)!size(rs)!})

最后要记得不同区间之间也有合并的贡献

我们现在要考虑修改：

1.((a,c))旋转后正好为((b,n))，就相当于将一棵树根节点的两个子树作为新的树，并且删除原来的根节点，对最小步数的影响为-1，对次数的影响也很简单（此处就不赘述，不会的珂以看代码）

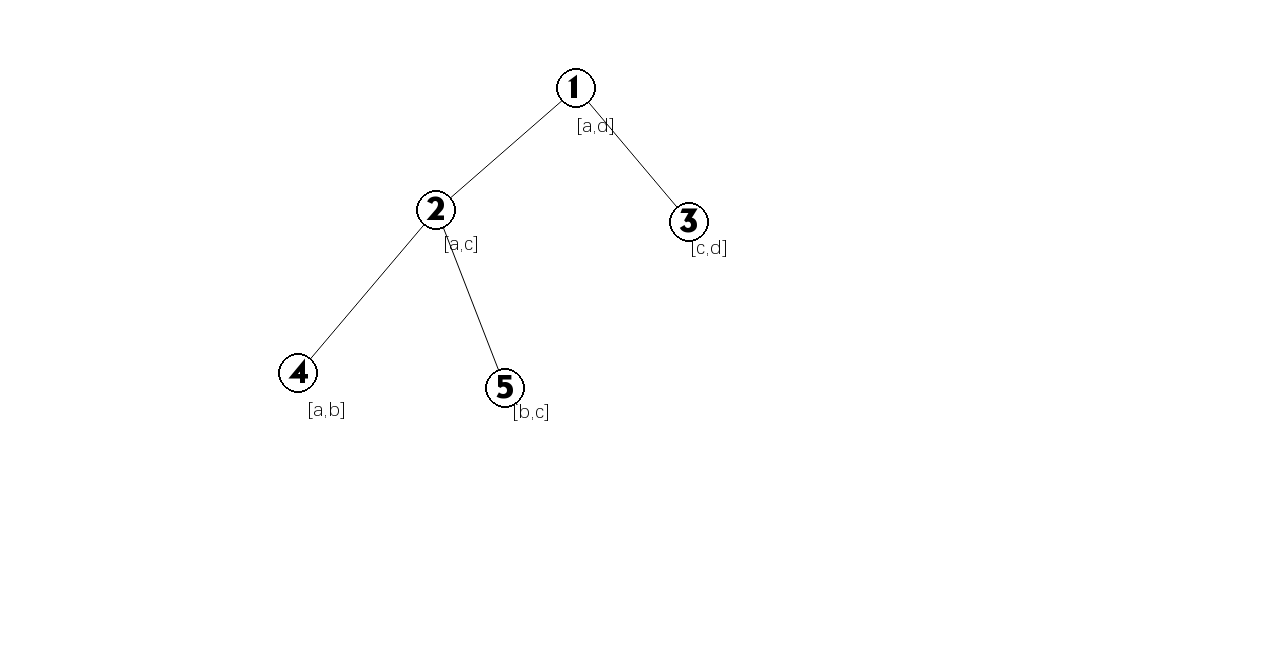
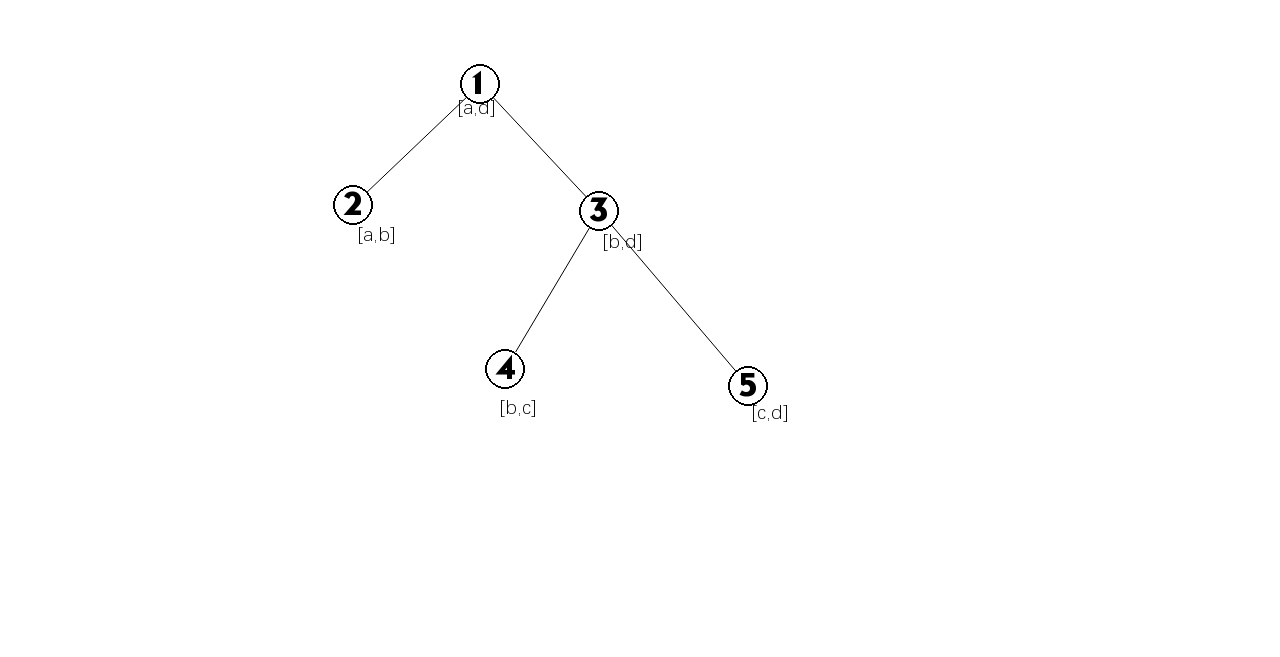
2.((a,c))旋转后变成了((b,d) (d eq n))，这个操作像splay的rotate，具体见图片，对最小步数没有影响，对次数的影响见代码

#include <bits/stdc++.h>
#define N 100005
#define mod 1000000007 
#define getchar nc
using namespace std;
inline char nc(){
    static char buf[100000],*p1=buf,*p2=buf;
    return p1==p2&&(p2=(p1=buf)+fread(buf,1,100000,stdin),p1==p2)?EOF:*p1++;
}
inline int read()
{
    register int x=0,f=1;register char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9')x=(x<<3)+(x<<1)+ch-'0',ch=getchar();
    return x*f;
}
inline void write(register int x)
{
    if(!x)putchar('0');if(x<0)x=-x,putchar('-');
    static int sta[20];register int tot=0;
    while(x)sta[tot++]=x%10,x/=10;
    while(tot)putchar(sta[--tot]+48);
}
inline int fastpow(register int a,register int b)
{
	int res=1;
	while(b)
	{
		if(b&1)
			res=1ll*res*a%mod;
		a=1ll*a*a%mod;
		b>>=1;
	}
	return res;
}
vector<int> E[N];
inline void add(register int u,register int v)
{
	E[u].push_back(v),E[v].push_back(u);
}
int W,n,m;
int fac[N],invf[N];
int fa[N],ls[N],rs[N],sz[N];
int tot=0,sum=0,ans=1;
map<pair<int,int>,int> M;
inline int calc(register int n,register int m)
{
	return 1ll*fac[n+m]*invf[n]%mod*invf[m]%mod;
}
inline int calcinv(register int n,register int m)
{
	return 1ll*invf[n+m]*fac[n]%mod*fac[m]%mod;
}
inline void dfs(register int &x,register int l,register int r,register int f)
{
	if(l+1==r)
		return;
	x=++tot;
	M[make_pair(l,r)]=x;
	fa[x]=f;
	int mid=*(--lower_bound(E[l].begin(),E[l].end(),r));
	dfs(ls[x],l,mid,x),dfs(rs[x],mid,r,x);
	sz[x]=sz[ls[x]]+sz[rs[x]]+1;
	ans=1ll*ans*calc(sz[ls[x]],sz[rs[x]])%mod;
}
int main()
{
	fac[0]=1;
	for(register int i=1;i<N;++i)
		fac[i]=1ll*fac[i-1]*i%mod;
	invf[N-1]=fastpow(fac[N-1],mod-2);
	for(register int i=N-1;i;--i)
		invf[i-1]=1ll*invf[i]*i%mod;
	W=read(),n=read();
	for(register int i=1;i<n;++i)
		add(i,i+1);
	add(1,n);
	for(register int i=1;i<=n-3;++i)
	{
		int u=read(),v=read();
		add(u,v);
	}
	for(register int i=1;i<=n;++i)
		sort(E[i].begin(),E[i].end());
	for(register int i=0;i<E[n].size()-1;++i)
	{
		int x=0;
		dfs(x,E[n][i],E[n][i+1],0);
		ans=1ll*ans*calc(sum,sz[x])%mod;
		sum+=sz[x];
	}
	if(W)
		write(sum),putchar(' '),write(ans),puts("");
	else
		write(sum),puts("");
	m=read();
	while(m--)
	{
		int a=read(),b=read(),x=M[make_pair(a,b)];
		if(fa[x])
		{
			int f=fa[x],now=ans;
			now=1ll*now*calcinv(sz[ls[x]],sz[rs[x]])%mod;
			now=1ll*now*calcinv(sz[ls[f]],sz[rs[f]])%mod;
			now=1ll*now*calc(sz[rs[x]],sz[rs[f]])%mod;
			now=1ll*now*calc(sz[ls[x]],sz[rs[x]]+sz[rs[f]]+1)%mod;
			if(W)
				write(sum),putchar(' '),write(now),puts("");
			else
				write(sum),puts("");
		}
		else
		{
			int now=ans;
			now=1ll*now*calcinv(sz[ls[x]],sz[rs[x]])%mod;
			now=1ll*now*calcinv(sum-sz[x],sz[x])%mod;
			now=1ll*now*calc(sum-sz[x],sz[ls[x]])%mod;
			now=1ll*now*calc(sum-sz[x]+sz[ls[x]],sz[rs[x]])%mod;
			if(W)
				write(sum-1),putchar(' '),write(now),puts("");
			else
				write(sum-1),puts("");
		}
	}
	return 0;
}