ZROI2018普转提day2t2

传送门

分析

我们发现2^R+C实际就相当于R行C列的子集的个数。因此我们可以将所有集合的子集个数转换为每个集合属于的集合的个数。所以我们可以求出：

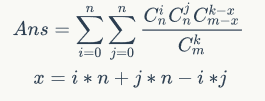
这个式子的意义为对于选i行j列的情况的所有方案乘上i行j列的情况出现的概率（这个就是算了它被几个集合包含，因为剩下k-x个数也可能构成一些整行整列）。

注意因为double直接处理阶乘会爆炸所以我们要递推求解

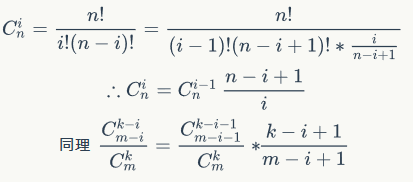
所以我们可以根据上式进行预处理，然后套公式求出Ans即可。

代码

#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<algorithm>
#include<cctype>
#include<cmath>
#include<cstdlib>
#include<ctime>
#include<queue>
#include<vector>
#include<set>
#include<map>
#include<stack>
using namespace std;
#define lb long double
lb ans,a[110000],b[110000];
int main(){
      int n,m,i,j,k;
      cin>>n>>m>>k;
      a[0]=b[0]=1;
      for(i=1;i<=m;i++){
          a[i]=a[i-1]*(n-i+1)/i;
          b[i]=b[i-1]*(k-i+1)/(m-i+1);
      }
      for(i=0;i<=n;i++)
        for(j=0;j<=n;j++){
           int x=i*n+j*n-i*j;
           if(x<=k){
                ans+=a[i]*a[j]*b[x];
           }
        }
      if(ans>=1e99)ans=1e99;
      printf("%Lf
",ans);
      return 0;
}