刷题算法总结 | LeetCode practice

前言：容易让人理解的文章行文方式应该是从特殊到一般也即从具体例子到抽象理论的过程。这里反其道而行，本文主要不是为了让人容易读懂，而是仅作为自己阅读的总结以备忘。

1、方法论

分治算法

将大问题分解为互不重叠的若干子问题，分别解决子问题后即完成大问题的解。

回溯算法

用来解决多阶段决策最优解问题

理论

回溯算法相当于穷举搜索：穷举所有的情况，然后对比得到最优解。通常是深度优先递归搜索。

回溯算法的时间复杂度通常非常高，是指数级别的，只能用来解决小规模数据的问题。对于大规模数据的问题，用回溯算法解决的执行效率就很低了。

解法模板：

（可参阅：https://github.com/labuladong/fucking-algorithm/blob/master/算法思维系列/回溯算法详解修订版.md）

回溯过程是穷举的过程，实际上就是决策树的遍历过程：开始时在根节点，每做一次决策就是选择往当前节点的某条边走从而进入某个子节点，当到达叶节点时停止，此时走过的各边组成的路径即为一个解。时间复杂度通常为决策树叶节点个数。

result = [] //路径列表
 backtrack(已选边列表, 可选边列表){
    if 满足结束条件:
        result.add(已选边列表)//得到一个解。也可直接打印该解，视题目要求；有时可能不需要所有解而是要最优解，这种情况只需保存截至当前的最优解并在此动态更新之
        return
    
    for 边 in 可选边列表{
        做选择：该边从可选列表移除并加入到已选列表
        backtrack(已选边列表, 可选边列表)
        撤销选择：撤销上述选择的操作
    }
}

回溯法穷举的时间复杂度高，但某些问题（如有些最优解问题）可以通过剪枝减少子问题的数量以提高时间效率，此即分支限界算法。

例1：全排列，以下两种实现本质上一样，都是上述模板的具体化，其时间都是复杂度O(n!)。

实现1：代码中用[s, curs)相当于已选择边列表、[curs, e]相当于可选择边列表。

代码：（参阅：https://www.cnblogs.com/z-sm/p/6857158.html）

void myFullPerm(int *data,int s,int curs,int e)//各参数分别为序列、序列起点下标、当前进行全排列的序列起点下标、序列终点下标。s ≤ curs ≤ e 
{
    if(s>curs || curs>e) return;
    
    int i;
    if(curs==e)
    {
        for(i=s;i<=e;i++) printf("%d ",data[i]);
        printf("
");
    }
    else
    {
        for(i=curs;i<=e;i++)
        {
            swap(data[curs],data[i]);//做选择
            myFullPerm(data,s,curs+1,e);//递归
            swap(data[curs],data[i]);//撤销选择
        }
    }
}

void swap(int &a,int &b)
{
    int tmp=a;
    a=b;
    b=tmp;
}

其对应的决策树为：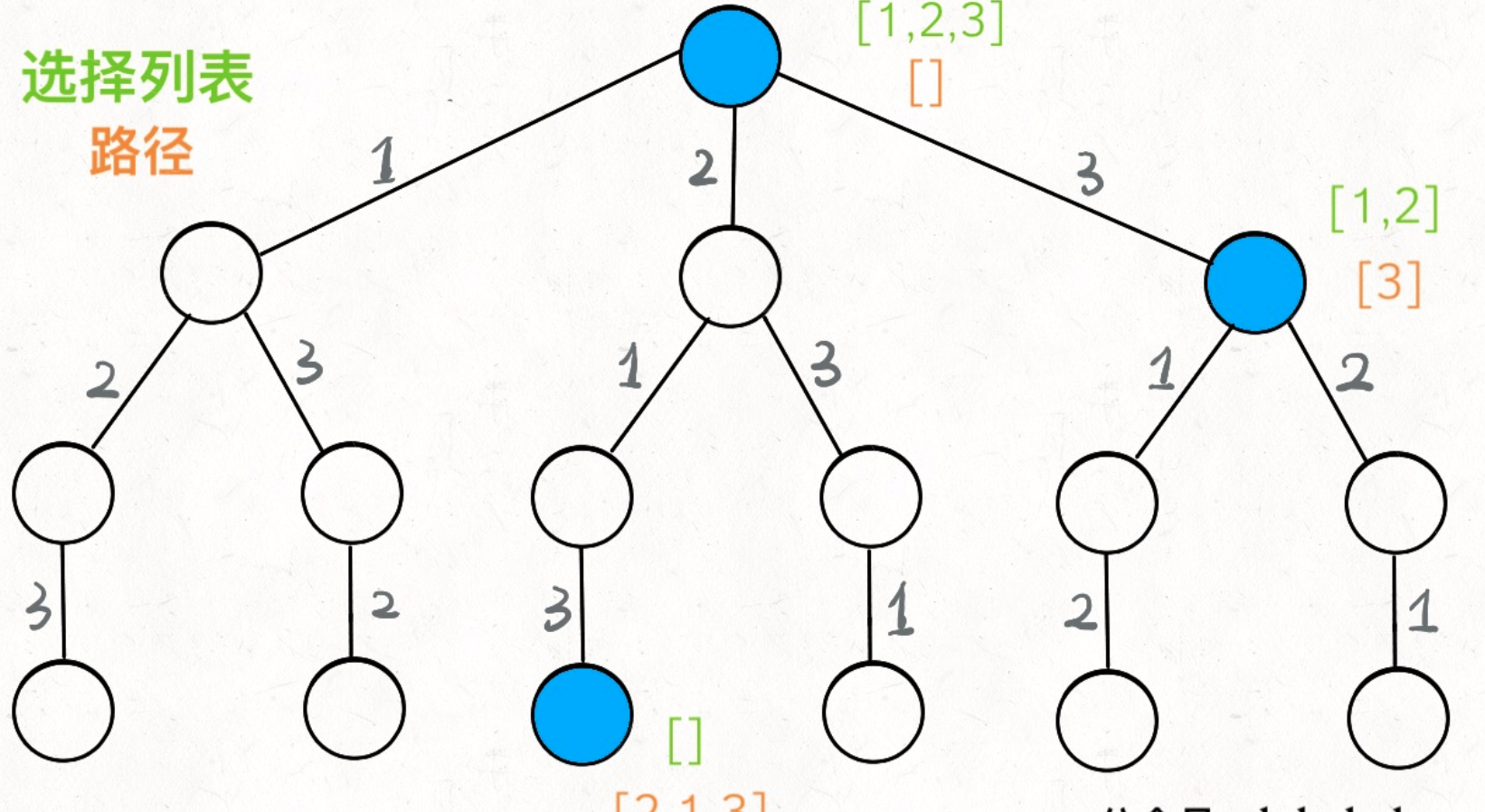

实现2：

代码：

List<List<Integer>> res = new LinkedList<>();

/* 主函数，输入一组不重复的数字，返回它们的全排列 */
List<List<Integer>> permute(int[] nums) {
    // 记录「路径」
    LinkedList<Integer> track = new LinkedList<>();
    backtrack(track, nums);
    return res;
}


// 结束条件：nums 中的元素全都在 track 中出现
void backtrack( LinkedList<Integer> track, int[] nums) {
    // 触发结束条件
    if (track.size() == nums.length) {
        res.add(new LinkedList(track));
        return;
    }
    
    for (int i = 0; i < nums.length; i++) {
        // 排除不合法的选择
        if (track.contains(nums[i]))
            continue;
        // 做选择
        track.add(nums[i]);
        // 进入下一层决策树
        backtrack(track, nums);
        // 取消选择
        track.removeLast();
    }
}

其对应的决策树为：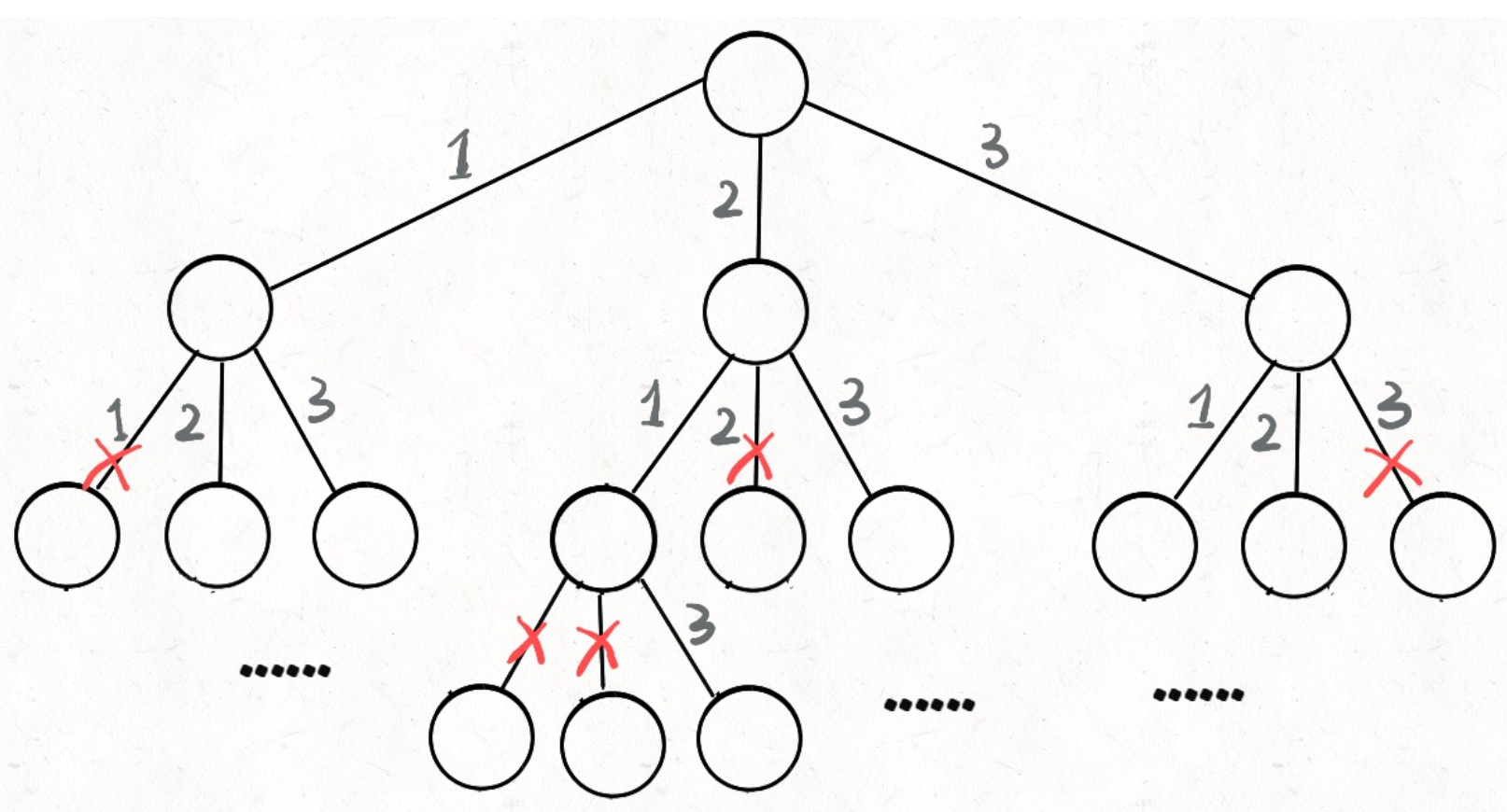

 例2：n皇后问题：将n个“皇后”摆在n*n的棋盘上使得皇后不能互相攻击（即对于一个皇后来说，其同行同列及同对角线上不存在其他皇后）。注，有些n下（如为2、3时）是无解的。

思路：从第1到n行依次放皇后，每次放置时检查与前面的行放置的皇后不冲突。

代码：

时间复杂度为O(nⁿ)。（与具体实现有关，可通过剪纸技巧减少时间复杂度，参阅：https://sites.google.com/site/nqueensolver/home/algorithm-results）

/* 输入棋盘边长 n，返回所有合法的放置 */
void solveNQueens(int n) {
    int selectedCols[n] = {-1};//初始为-1表示未选
backtrack(selectedCols, n, 0);
}

// selectedCols[i]：存储第i行中摆放皇后的列的位置
// row：将要对第row行选择一个列位置来摆放第(row+1)个皇后
void backtrack(int  selectedCols[], int n, int row) {
    // 触发结束条件
    if (row == n) {
        print selectedCols;
        return;
    }
    
    for (int col = 0; col < n; col++) {
        // 排除不合法选择
        if (!isValid(selectedCols, row, col)) 
            continue;
        // 做选择
        selectedCols[row] = col;
        // 进入下一行决策
        backtrack(selectedCols, n, row + 1);
        // 撤销选择
        selectedCols[row] = -1;
    }
}

/* 是否可以在（row, col)位置放置皇后？ */
bool isValid(int selectedCols[], int row, int col) {
    // 列检查：检查是否 与 前面已放置的各行上的皇后所处的列 冲突
    for (int i = 0; i < row; i++) {
        if (selectedCols[i] == col )
            return false;
    }
    // 检查右上方是否有皇后互相冲突
    for (int i = row - 1, j = col + 1; 
            i >= 0 && j < n; i--, j++) {
        if (selectedCols[i] == j )
            return false;
    }
    // 检查左上方是否有皇后互相冲突
    for (int i = row - 1, j = col - 1;
            i >= 0 && j >= 0; i--, j--) {
        if (selectedCols[i] == col )
            return false;
    }
    return true;
}

 

动态规划

用来解决多阶段决策最优解问题

理论

（可参阅：https://blog.csdn.net/qq_25800311/article/details/90635979）

一个模型——多阶段决策最优解模型：动态规划问题是求最优解的问题，解决问题的过程需要经历多个决策阶段。每个决策阶段都对应一组状态。然后我们寻找一组决策序列，经过这组决策序列，能够产生最终期望求解的最优值。

三个性质：适合用动态规划解决的问题必须有满足三个条件：

最优子结构：问题的最优解包含子问题的最优解。关于最优子结构，可参阅：https://github.com/labuladong/fucking-algorithm/blob/master/动态规划系列/最优子结构.md

子问题重叠：不同的决策序列，到达某个相同的阶段时，可能会产生一样的状态。

无后效性：当前阶段的状态由前面若干阶段的状态决定，且不必关心前面的这若干状态是怎么来的；某阶段的状态一旦确定就不受后面阶段决策的影响。这条一般都满足。

 解法：

（可参阅：https://github.com/labuladong/fucking-algorithm/blob/master/动态规划系列/动态规划详解进阶.md）

可以用动态规划解决的问题，解决的步骤：

定义状态变量的含义（通常考虑变量是一维或二维或更多维、包含或不包含当前元素）。

找出状态转移方程（类似数学中的递推式），这是关键点和难点。

确定base case。

根据递推式实现（自顶向下或自底向上）。

根据递推式实现，即将递推式翻译成代码：

1、回溯法（穷举法）：时间复杂度为 子问题个数 * 每个子问题的时间复杂度

能用动态规划解决的也能用回溯法解决——即将递推式翻译成代码即可，代码通常是递归算法，其时间复杂度通常很高（因重复计算子问题）。

2、动态规划算法：根据状态转移方程，通常有两法求解动态规划问题，与暴力解法相比其主要原理是借助“备忘录”（可以是数组、Map等）记住当前问题的结论以免重复计算当前问题。

（1）自顶向下递归的“备忘录”法：将递推式翻译成代码，只不过进一步借助“备忘录”记住当前问题的结论，因当前问题会重叠故再遇到时直接从“备忘录”取结论而不用重复计算。解决问题为主，构造备忘录为辅。

自底向上实现时要注意的是base case应该初始化谁、以及变量迭代方向，这与递推式有关，结论是：应初始化与变量递推方向相反的值；变量也按与递推相反方向迭代。如：若dp(i, j)=dp(i-1,j-1)+... 则初始化左上角、i和j均从小到大；若dp(i,j)=dp(i+1, j-1)+... 则初始化左下角、i从大到小j从小到大，可看后面最长回文子串示例。

（2）自底向上非递归“备忘录”法：从小的子问题到大的子问题依次迭代计算，也借助“备忘录”记住当前问题的结论，当计算更大问题过程中用到子问题时就可从“备忘录”获取子问题结论而不用重复计算。构造备忘录为主，附带借助备忘录得到问题解。

通常自底向上者比较容易理解；并不是所有动态规划问题在有了状态转移方程后都可轻易用三种方法解决，特别是自底向上者有时不易实现。

计算机解决问题其实没有技淫巧，它唯一的解决办法就是穷举，穷举所有可能性，算法设计无非就是先思考“如何穷举”，然后再追求“如何聪明地穷举”。找状态转移方程就是在解决如何穷举、动态规划的备忘录就是在解决如何聪明地穷举，因此动态规划本质上也是穷举，只不过通过空间换时间来降低时间复杂度。

例1：斐波那契数列

其状态转移方程为：f(n)=f(n-1)+f(n-2)且n>2、f(1)=1、f(2)=2

1、回溯法（穷举解法）：

时间复杂度O(2ⁿ)、空间复杂度O(1)

int fib(int N) {
    if (N == 1 || N == 2) return 1;
    return fib(N - 1) + fib(N - 2);
}

2、自顶向下：与暴力法很像，只不过多了查备忘录的步骤以免重复计算重叠的子问题

时间复杂度O(n)、空间复杂度O(n)

int fib(int N) {
    if (N < 1) return 0;
    // 备忘录全初始化为 0
    vector<int> memo(N + 1, 0);
    // 初始化最简情况
    return helper(memo, N);
}
 
int helper(int  memo[], int n) {
    // base case 
    if (n == 1 || n == 2) return 1;
    // 已经计算过
    if (memo[n] != 0) return memo[n];
    memo[n] = helper(memo, n - 1) + 
                helper(memo, n - 2);
    return memo[n];
}

3、自底向上：

时间复杂度O(n)、空间复杂度O(n)

int fib(int N) {
    vector<int> dp(N + 1, 0); //初始化为全0
    // base case
    dp[1] = dp[2] = 1;
    for (int i = 3; i <= N; i++)
        dp[i] = dp[i - 1] + dp[i - 2];
    return dp[N];
}

有些情况下，自底向上方法中的“备忘录”可以不用数组而是用几个变量即可，此时时间复杂度O(n)、空间复杂度O(1)

int fib(int n) {
    if (n == 2 || n == 1) 
        return 1;
    int prev = 1, curr = 1;
    for (int i = 3; i <= n; i++) {
        int sum = prev + curr;
        prev = curr;
        curr = sum;
    }
    return curr;
}

例2：矩阵左上角到右下角的最短路径（权值和最小的路径）

状态转移方程为：f(i,j)=matrix[i][j]+ min{ f(i-1,j), f(i,j-1) }，f(i,j)表示(0,0)到(i, j)的最短路径的长度，其中，i∈[0,m], j∈[0,n]

1、回溯法（穷举解法）：

时间复杂度O(2^mn)、空间复杂度O(1)

//调用minDist(n-1,n-1)
int minDist(int i, int j) {
    if (i == 0 && j == 0) return matrix[0][0];
    //if (mem[i][j] > 0) return mem[i][j];//有此步的话则为动态规划递归算法
 
    int minLeft = INT_MAX;
    if (j - 1 >= 0) {
        minLeft = minDist(i, j - 1);
    }
 
    int minUp = INT_MAX;
    if (i - 1 >= 0) {
        minUp = minDist(i - 1, j);
    }
 
    int curMinDIst = matrix[i][j] + min(minLeft, minUp);
    mem[i][j] = curMinDIst;
    return curMinDIst;
}

2、自顶向下：与暴力法很像，只不过多了查备忘录的步骤以免重复计算重叠的子问题

时间复杂度O(mn)、空间复杂度O(mn)

//调用minDist(n-1,n-1)
int minDist(int i, int j) {//mem[][]为备忘录，初始为全0
    if (i == 0 && j == 0) return matrix[0][0];
    if (mem[i][j] > 0) return mem[i][j];
 
    int minLeft = INT_MAX;
    if (j - 1 >= 0) {
        minLeft = minDist(i, j - 1);
    }
 
    int minUp = INT_MAX;
    if (i - 1 >= 0) {
        minUp = minDist(i - 1, j);
    }
 
    int curMinDIst = matrix[i][j] + min(minLeft, minUp);
    mem[i][j] = curMinDIst;
    return curMinDIst;
}

3、自底向上：

时间复杂度O(mn)、空间复杂度O(mn)

int minDistDP(const vector<vector<int>> &matrix, int m, int n) {
    vector<vector<int>> mem;
    int sum = 0;
    for (int j = 0; j < n; ++j) {//初始化mem的第一列数据
        sum += matrix[0][j];
        mem[0][j] = sum;
    }
 
    sum = 0;
    for (int i = 0; i < m; ++i) { //初始化mem的第一行数据
        sum += matrix[i][0];
        mem[i][0] = sum;
    }
 
    for (int i = 1; i < m; ++i) {
        for (int j = 1; j < n; ++j) {
            mem[i][j] = matrix[i][j] + min(mem[i - 1][j], states[i][j - 1]);
        }
    }
 
    return mem[n - 1][n - 1];
}

例3：给定k种面值各不相同的硬币coins[k]，每种硬币有无限多个，求凑得总金额amount的最少硬币数dp[amount]，不可能凑出则返回-1。

状态转移方程：f(n)=1+ min{ f(n-coins[i]) }，其中i∈[0, k-1]、n=0时f(n)=0、n<0时f(n)=-1

回溯法、自顶向下、自底向上三种方法：

//回溯法
int minCoinCount(int coins[], int k, int amount){//-1表示不存在方案
    if(amount==0) return 0;
    if(amount<0 || k<=0) return -1;

    int minRes = INT_MAX, tmpRes;
    for (int i=0;i<k;i++):
        if(amount >= conins[i]){
            tmpRes = minCoinCount(coins,k,amount-coins[i]);
            if(-1==tmpRes) continue;
            tmpRes+=1;
            if(minRes>tmpRes) minRes=tmpRes;
        }
    minRes= INT_MAX==minRes?-1:minRes;//amount<0情况也会被此处理到，故可不用对该情况特殊处理
    return minRes;
}

//自顶向下
int mem[amount+1]={-2};//-2表示未赋值
int minCoinCount(int coins[], int k, int amount){//不存在方案则返回-1

    if(amount==0) return 0;
    if(amount<0 || k<=0) return -1;

    if(mem[amount]!=-2) return mem[amount];

    int minRes = INT_MAX, tmpRes;
    for (int i=0;i<k;i++):
        if(amount >= conins[i]){
            tmpRes = minCoinCount(coins,k,amount-coins[i]);
            if(-1==tmpRes) continue;
            tmpRes+=1;
            if(minRes>tmpRes) minRes=tmpRes;
        }
    minRes= INT_MAX==minRes?-1:minRes;
    mem[amount]=minRes;
    return minRes;
}


//自底向上
int mem[amount+1]={-2};
int minCoinCount(int coins[], int k, int amount){//不存在方案则返回-1
    mem[0]=0;
    for(int i=1;i<=amount;i++){//从前往后为mem赋值
        mem[i]=INT_MAX;
        for(int j=0;j<k;j++){
            if(i>=coins[j] && -1!=mem[i-coins[j]]){
                if(mem[i]>mem[i-coins[j]]+1)
                    mem[i]=mem[i-coins[j]]+1;
            }
        }
        mem[i]= INT_MAX==mem[i]?-1:mem[i];
    }
}

注意，通常最优解问题才可用动态规划解决，如 最大子段和问题 可用动态规划解决、而 和等于k的子段数 问题则不用动态规划而是用前缀和解决。

贪心算法

用来解决多阶段决策最优解问题

在解决问题时总是选择当前阶段的最优解，即贪心选择，通过所有阶段都选择局部最优解，最终产生全局最优解。贪心算法际上是动态规划算法的一种特殊情况。它解决问题起来更加高效，代码实现也更加简洁。不过，它可以解决的问题也更加有限。

能用贪心算法解决的问题需要满足三个条件：最优子结构、无后效性、贪心选择性

分治、贪心、回溯、动态规划算法的区别

贪心、回溯、动态规划可以归为一类，而分治单独可以作为一类，因为它跟其他三个都不大一样。为什么这么说呢？前三个算法解决问题的模型，都可以抽象成我们多阶段决策最优解模型，而分治算法解决的问题尽管大部分也是最优解问题，但是，大部分都不能抽象成多阶段决策模型。

回溯算法是个“万金油”。基本上能用的动态规划、贪心解决的问题，我们都可以用回溯算法解决。回溯算法相当于穷举搜索。穷举所有的情况，然后对比得到最优解。不过，回溯算法的时间复杂度非常高，是指数级别的，只能用来解决小规模数据的问题。对于大规模数据的问题，用回溯算法解决的执行效率就很低了。

尽管动态规划比回溯算法高效，但是，并不是所有问题，都可以用动态规划来解决。能用动态规划解决的问题，需要满足三个特征，最优子结构、无后效性和重复子问题。在重复子问题这一点上，动态规划和分治算法的区分非常明显。分治算法要求分割成的子问题，不能有重复子问题，而动态规划正好相反，动态规划之所以高效，就是因为回溯算法实现中存在大量的重复子问题。

贪心算法实际上是动态规划算法的一种特殊情况。它解决问题起来更加高效，代码实现也更加简洁。不过，它可以解决的问题也更加有限。它能解决的问题需要满足三个条件，最优子结构、无后效性和贪心选择性（这里我们不怎么强调重复子问题）。其中，最优子结构、无后效性跟动态规划中的无异。“贪心选择性”的意思是，所求问题的整体最优解可以通过一系列局部最优的选择来达到，通过局部最优的选择能产生全局的最优选择。每一个阶段，我们都选择当前看起来最优的决策，所有阶段的决策完成之后，最终由这些局部最优解构成全局最优解。

树/图相关算法（遍历、建立等）

见 https://www.cnblogs.com/z-sm/p/6917749.html

并查集算法

见 https://www.cnblogs.com/z-sm/p/12383918.html

排序算法

见 https://www.cnblogs.com/z-sm/p/6914667.html

洗牌算法

见 https://www.cnblogs.com/z-sm/p/12393211.html

FloodFill算法

（可参阅：https://github.com/labuladong/fucking-algorithm/blob/master/算法思维系列/FloodFill算法详解及应用.md）

what：

比如一张图片里选择某个像素后相邻的同颜色像素也都被选中，成为一个区域，从而实现同颜色区域的选择或染色。扫雷游戏、消消乐游戏、绘图软件的区域选取及颜色填充等都用到此算法。

算法模板：

（输入是二维矩阵，初始从某个点开始访问，递归地向该点的四周扩展访问，直到无法扩展为止，其实相当于四叉树的深度优先前序递归遍历）

int[][] floodFill(int[][] image,
        int srow, int scol, int newColor) {

    int origColor = image[srow][scol];
    fill(image, srow, scol, origColor, newColor);//旧新颜色参数允许一样
    return image;
}

//借助if(origColor==newColor) 来处理旧新颜色一样时递归停不下的问题
void fill(int[][] image, int x, int y,
        int origColor, int newColor) {
    // 参数验证：超出边界
    if (!(x >= 0 && x < image.length
        && y >= 0 && y < image[0].length)) return;

    // 旧新颜色不一样且当前像素需要被替换
    if (image[x][y] == origColor)
    {
        //旧新颜色一样，不用替换
        if(origColor==newColor) return;

        image[x][y] = newColor;
        fill(image, x, y + 1, origColor, newColor);
        fill(image, x, y - 1, origColor, newColor);
        fill(image, x - 1, y, origColor, newColor);
        fill(image, x + 1, y, origColor, newColor);
    }
}

//借助replaced[][]数组来处理旧新颜色一样时递归停不下的问题，用于标记是否已被替换
void fill(int[][] image, int x, int y,
        int origColor, int newColor, int [][]visited) {
    // 参数验证：超出边界
    if (!(x >= 0 && x < image.length
        && y >= 0 && y < image[0].length)) return;


    // 旧新颜色不一样且当前像素需要被替换
    if (image[x][y] == origColor)
    {
        if(replaced[x][y]) return;

        image[x][y] = newColor;
        replaced[x][y]=true;
        fill(image, x, y + 1, origColor, newColor);
        fill(image, x, y - 1, origColor, newColor);
        fill(image, x - 1, y, origColor, newColor);
        fill(image, x + 1, y, origColor, newColor);
    }
}

对于区域内的像素，当访问像素a时，该像素四周的也会被访问，而分别访问四周的像素时也会访问到a，故区域内的每个像素会被访问 (1+四周同颜色像素数) 遍，大多为5。

当旧新颜色一样时，会在当前像素和四周像素间来回递归停不下来，处理方法有两种：判断旧新颜色不一样、借助标记数组，分别对应上述两种代码实现。

拓展：很多绘图软件有抠图功能，其可以选择图像中的前景物体或背景，这与上述染色的区别有二：1是被选择出来的区域中各像素颜色并不完全相同、2是并不对区域染色而是只对边界染色。

解决：

对于第一点可以定义个阈值，将像素值差在阈值内的颜色视为同一种。 return Math.abs(image[x][y] - origColor) <= threshold; //判断某像素是否得被染色 

对于第二点其实就是找区域的边界：对区域内的一个像素来说，其值与上下左右的像素的值相同，而边界的像素则非如此，可据此找出边界像素并对其染色即可。

代码：（基于第二种实现稍加修改即可）

int[][] floodFill(int[][] image,
        int srow, int scol, int newColor) {

    int origColor = image[srow][scol];
    fill(image, srow, scol, origColor, newColor);//旧新颜色参数允许一样
    return image;
}

//借助replaced[][]数组来处理旧新颜色一样时递归停不下的问题，用于标记是否已被替换
void fill(int[][] image, int x, int y,
        int origColor, int newColor, int [][]visited) {
    // 参数验证：超出边界
    if (!(x >= 0 && x < image.length
        && y >= 0 && y < image[0].length)) return;


    // 旧新颜色不一样且当前像素需要被替换
    if (image[x][y] == origColor)
    {
        if(replaced[x][y]) return;

        replaced[x][y]=true;
    
        fill(image, x, y + 1, origColor, newColor);
        fill(image, x, y - 1, origColor, newColor);
        fill(image, x - 1, y, origColor, newColor);
        fill(image, x + 1, y, origColor, newColor);

        //边界元素有没被替换的则说明当前像素是区域的边界
        if( !(replaced[x][y+1] && replaced[x][y-1] && replaced[x+1][y] && replaced[x-1][y] ) ) {
            image[x][y] = newColor;
        }
    }
}

有序数组的二分查找算法

用于从一个有序元素序列中找出与给定值一样的元素的位置。当给定元素在元素序列中存在时，根据元素是否唯一，可以有三种查找方式：

唯一时：普通的二叉查找，如从 [1, 2, 3, 5, 6]中查找2

不唯一时：返回最左边元素、返回最右边元素，如，如从 [1, 2, 2, 2, 3, 5, 6]中查找2时要求返回最左边的2或最右边的2的位置

代码实现比较简单，这里要强调的是如何深刻理解并容易记忆这个代码的细节：

//由于初始left=0,right=len-1，故搜索范围为[left, right]，从而结束时left=right+1
int binarySearch(int[] nums, int target) {
    int left = 0, right = nums.length - 1; 
    while(left <= right) {//搜索范围内
        int mid = left + (right - left) / 2;
        if (nums[mid] < target) {
            left = mid + 1;
        } else if (nums[mid] > target) {
            right = mid - 1; 
        } else if(nums[mid] == target) {
            // 直接返回
            return mid;
        }
    }
    // 直接返回
    return -1;
}

int leftBinarySearch(int[] nums, int target) {
    int left = 0, right = nums.length - 1;
    while (left <= right) {//搜索范围内
        int mid = left + (right - left) / 2;
        if (nums[mid] < target) {
            left = mid + 1;
        } else if (nums[mid] > target) {
            right = mid - 1;
        } else if (nums[mid] == target) {
            // 找到，right左移
            right = mid - 1;
        }
    }

    //由于right左移，故若找到则可能位置只能为left
    if (left >= nums.length || nums[left] != target)// 未找到的情况：越界或未找到
        return -1;
    else //找到
        return left;
}


int rightBinarySearch(int[] nums, int target) {
    int left = 0, right = nums.length - 1;
    while (left <= right) {//搜索范围内
        int mid = left + (right - left) / 2;
        if (nums[mid] < target) {
            left = mid + 1;
        } else if (nums[mid] > target) {
            right = mid - 1;
        } else if (nums[mid] == target) {
            // 找到，left右移
            left = mid + 1;
        }
    }

    //由于left右移，故若找到则可能位置只能为right
    if (right < 0 || nums[right] != target)// 未找到的情况：越界或未找到
        return -1;
    else //找到
        return right;
}

注：

1、判断找到时是取left还是right的方法：以只有一个元素且该元素即为所要找到为例即可。

2、考虑的越界条件：待查元素比序列中所有元素大或小的场景

3、循环的条件为“处于搜索范围时”，结束的条件是“不在搜索范围”，范围的具体值取决于left、right的初始定义，上面代码中分别为元素的始终值，即[0、len-1]。

下面以左闭右开形式定义“范围”即[0, len) 来实现上述三个算法的等价形式，代码如下：

//由于初始left=0,right=len，故搜索范围为[left, right)，从而结束时left=right
int binarySearch(int[] nums, int target) {
    int left = 0, right = nums.length; //nums.length - 1; 
    while(left<right){ //while(left <= right) {
        int mid = left + (right - left) / 2;
        if (nums[mid] < target) {
            left = mid + 1;
        } else if (nums[mid] > target) {
            right = mid; //mid - 1; 
        } else if(nums[mid] == target) {
            // 直接返回
            return mid;
        }
    }
    // 直接返回
    return -1;
}

int leftBinarySearch(int[] nums, int target) {
    int left = 0, right = nums.length; //nums.length - 1;
    while(left<right){ //while (left <= right) {
        int mid = left + (right - left) / 2;
        if (nums[mid] < target) {
            left = mid + 1;
        } else if (nums[mid] > target) {
            right = mid; //mid - 1;
        } else if (nums[mid] == target) {
            right = mid; //mid - 1;
        }
    }

    //由于right左移，故若找到则可能位置只能为left
    if (left >= nums.length || nums[left] != target)// 未找到的情况：越界或未找到
        return -1;
    else //找到
        return left;
}


int rightBinarySearch(int[] nums, int target) {
    int left = 0, right = nums.length; //nums.length - 1;
    while(left<right){ //while (left <= right) {
        int mid = left + (right - left) / 2;
        if (nums[mid] < target) {
            left = mid + 1;
        } else if (nums[mid] > target) {
            right = mid; //mid - 1;
        } else if (nums[mid] == target) {
            left = mid + 1;
        }
    }

    right--;//因right是开的故结束时可转为闭的算法的情形

    //由于left右移，故若找到则可能位置只能为right
    if (right < 0 || nums[right] != target)// 未找到的情况：越界或未找到
        return -1;
    else //找到
        return right;
}

参考资料：https://github.com/labuladong/fucking-algorithm/blob/master/算法思维系列/二分查找详解.md

 

2、具体问题归类总结 

0、双指针（滑动窗口）

判断单链表是否有环：快慢指针相遇则说明有环。

分析：

慢指针每次走1步、快指针每次走2步，则当慢者走k步（即边数）时快者多走了k步；

当两者相遇时慢者肯定没走完环；且快者比慢者多的刚好是环长（边数）的n倍：若环边数比环前的边数多很多则是1倍，否则可能是多倍

代码：

boolean hasCycle(ListNode head) {
    ListNode fast, slow;
    fast = slow = head;
    while (fast != null && fast.next != null) {
        fast = fast.next.next;
        slow = slow.next;
        
        if (fast == slow) return true;
    }
    return false;
}

找出含环的单链表中环的起始节点：相遇时分别从相遇节点和单链表起始节点开始，每次走一步，直到再次相遇时即是环起始节点

分析：

基于上面的结论，进一步地，相遇时假设环起始节点到相遇节点有m步，则单链表起始节点到环起始节点有k-m（慢者步数k减去m）；

而由于第一次相遇时快者比慢者多走的k步是环长的倍数，故从该相遇点再走k-m步也将到达环起始节点（此过程绕了环n-1圈）

代码：（与上面的类似）

ListNode detectCycle(ListNode head) {
    ListNode fast, slow;
    fast = slow = head;
    while (fast != null && fast.next != null) {
        fast = fast.next.next;
        slow = slow.next;
        if (fast == slow) break;
    }

    slow = head;
    while (slow != fast) {
        fast = fast.next;
        slow = slow.next;
    }
    return slow;
}

 找出单链表的中间节点：快慢指针每次分别走1、2步，当快指针为null时慢者即为中点

ListNode findMiddleNode(ListNode head) {
    ListNode fast, slow;
    fast = slow = head;
    while (fast != null && fast.next != null) {
        fast = fast.next.next;
        slow = slow.next;        
    }
    return slow; //slow位置：节点数为奇数时在中，偶数时中偏右
}

找出单链表的倒数第k个节点：快慢指针，快指针先行k步，然后两指针同速前行，快者为null时慢者即为所求

ListNode reverseKthNode(ListNode root, int k){// k= 1,2, ... , n
  ListNode slow, fast;
  slow = fast = head;
  while (k-- > 0 && fast!=null) {
      fast = fast.next;
  }
  if(0!=k) return null;

  while (fast != null) {
      slow = slow.next;
      fast = fast.next;
  }
  return slow;
}

其他双指针问题：有序数组二分查找（见前面一节）、有序数组two sum问题、反转数组等。有序数组two sum问题示例：

int[] twoSum(int[] nums, int target) {
    int left = 0, right = nums.length - 1;
    while (left < right) {
        int sum = nums[left] + nums[right];
        if (sum == target) {
            return new int[]{left, right};
        } else if (sum < target) {
            left++; // 让 sum 大一点
        } else if (sum > target) {
            right--; // 让 sum 小一点
        }
    }
    // 不存在这样两个数
    return new int[]{-1, -1};
}

滑动窗口：解题有大概的模板，分析可参阅“滑动窗口技巧及解题模板”

最短覆盖子串：从字符串S中找出包含 字符串P中所有字符（P中字符可能有重） 的最短子串，即LeetCode-76

class Solution {
    public String minWindow(String s, String t) {
        int resStart = 0, minLen = Integer.MAX_VALUE;//结果信息

        Map<Character, Integer> windowChCntMap = new HashMap<>();//窗口信息
        Map<Character, Integer> patternChCntMap = new HashMap<>();
        int left = 0, right = 0, matchCnt = 0;//双指针

        char ch;
        // 初始化patternChCntMap
        for (int i = t.length() - 1; i >= 0; i--) {
            ch = t.charAt(i);
            patternChCntMap.put(ch, patternChCntMap.getOrDefault(ch, 0) + 1);
        }
        // 滑动右边界
        while (right < s.length()) {
            ch = s.charAt(right);
            // 若右边界字符有效：窗口右字符是pattern中的字符
            if (patternChCntMap.containsKey(ch)) {
                // 更新窗口记录信息
                int chCntInWindow = windowChCntMap.getOrDefault(ch, 0) + 1;
                windowChCntMap.put(ch, chCntInWindow);
                if (chCntInWindow == patternChCntMap.get(ch)) {
                    matchCnt++;

                    // 若找到匹配的覆盖串
                    while (matchCnt == patternChCntMap.size()) {
                        // 更新结论
                        if (right - left + 1 < minLen) {
                            resStart = left;
                            minLen = right - left + 1;
                        }
                        // 滑动左边界
                        ch = s.charAt(left);
                        if (patternChCntMap.containsKey(ch)) {
                            chCntInWindow = windowChCntMap.get(ch) - 1;
                            windowChCntMap.put(ch, chCntInWindow);
                            if (chCntInWindow < patternChCntMap.get(ch)) {
                                matchCnt--;
                            }
                        }
                        left++;
                    }
                }

            }
            right++;
        }
        return minLen == Integer.MAX_VALUE ? "" : s.substring(resStart, resStart + minLen);
    }
}

最长不重复子串：即LeetCode-3

class Solution {
    public int lengthOfLongestSubstring(String s) {
        int resStart=0,maxLen=0;//结果信息

        Set<Character> chSet= new HashSet<>();//窗口信息

        int left=0,right=0;
        char ch;
        //滑动右边界
        while(right<s.length()){
            ch=s.charAt(right);
            //当前右边界字符有效
            if(!chSet.contains(ch)){
                //更新窗口信息
                chSet.add(ch);
                //更新结论
                if(maxLen<right-left+1){
                    resStart=left;
                    maxLen=right-left+1;
                }
            }else{
                //滑动左边界
                while(s.charAt(left)!=ch){
                    chSet.remove(s.charAt(left));
                    left++;
                }
                left++;
            }
            right++;
        }
        return maxLen;
    }
}

 最长递增子串：见后文 “字符串问题-子段” 一节

  

1、位操作妙用

位操作的若干技巧见：https://www.cnblogs.com/z-sm/p/3864107.html 中的节31处

整数二进制形式中1的个数（LeetCode-338）

给定一非负Integer num，求[0,num]每个数的二进制形式中1的个数  f[num+1]。

解法：可用最朴素的方法逐个求，但其实有规律： f[i] = f[i / 2] + i % 2 或  f[i] = f[i&(i-1)] + 1; 

2、Single Number

一组Integer类型的数，除了一个出现N次外，其他都出现M次，找出此数（N ≠ M）。（相关题目：https://leetcode.com/problems/single-number-ii/#/description）

法1：排序，时间复杂度最少O(nlgn)

法2：利用哈希表计每个数出现此时，时间复杂度近似O(n)，空间复杂度为O(n)

法3：（推荐）思路：每个Integer32位，对于每一位，各个数该位上的值的和对M求模，结果即为特殊的数在该位上的和的N倍（若N>M则为 N%M倍）。时间复杂度为O(n)，空间复杂度为O(1)

代码如下：

    public int singleNumber(int[] nums, int M, int N) {// with constant memory
        int res = 0;
        int tmpCurBitSum = 0;
        for (int bit = 0; bit < 32; bit++) {
            tmpCurBitSum = 0;
            for (int i : nums) {
                tmpCurBitSum += ((1 << bit) & i) >>> bit;
            }
            res |= ((tmpCurBitSum % M)/(N%M)) << bit;
        }
        return res;
    }

特殊情况：M为偶数，N为奇数，如当M=2，N=1时候即为经典的题“除了一个数出现一次外其他数都出现2次”，此时还可以用更简单的方法：所有数异或，结果即为特殊数。

题目变换：有两个分别出现奇数次，其他的都出现偶数次。仍可以用法1或法2解决，但空间复杂度高；另法：所有数异或得到特殊的那两个数的异或值a，对于a中值为1的位，在原两数中该位上的值肯定不同，故可选一位将所有数分成两组，两特殊数分别在两组中，两组各自异或得到两个数即为结果。（相关题目：https://leetcode.com/problems/single-number-iii/#/solutions）

3、子段/子序列问题

假设有数组 a[1, 2, ..., n]，引入如下概念：

子段：a的子数组，为连续的若干个元素，如 a[3, 4, 5] 。子串：当a是字符串时子段也称为子串。

子序列：a的若干个元素组成的数组，不要求元素连续，如 a[1, 3, 4]

问题分类：根据a的元素“当成 ”数值还是字符处理，子段、子序列问题均可分为两类：[ 子段、子序列 ] * [ 数值、字符 ]。注意这里是“当成”，也就是说跟题意有关：如对于a=[3, 2, 4, 5, 1]，虽元素是数值，但既可以求最大子段和、又可以求最长不重复子段，后者就是“当成”字符处理。

解决方法：子段、子序列问题大多可用动态规划解决。当然，有旳问题还有更好的解决方式，如有些子段和问题用前缀和、有些子串问题用滑动窗口解决更好。

注：子段也是种特殊的子序列，反之则不是。

3.1 数值问题-子段/子序列

子段和用动态规划或前缀和解决；用动态规划时，对于子段问题假设的状态变量通常包含当前末尾元素、对于子序列问题则否，不过并不绝对。

1、子段/子序列和的最大值

1、最大子段和（一个子段）：设 b[j] 为 a[1,2,...,j] 包含 a[j] 的最大子段和，根据子段是否仅包含a[j]有（也可根据b[j-1]是否大于0得到）： b[j] = max{a[j], b[j-1]+a[j] } 

int maxSum(int n,int *a)
{
  int sum=0,b=0;
  for(int i=0;i<n;i++)
  {
    if(b>0) b+=a[i];
    else b=a[i];
    if(sum<b) sum=b;
  }
  return sum;
}

这实际上是下面最大m子段和问题的特例。

2、最大m子段和（找出m个子段，可以相邻）：设 b[i,j] 为 a[1,2,...,j] 前j项中i个子段的最大和且第i个子段包含a[j]（1≤i≤m, i≤j≤n），则根据第i个子段是否仅仅包含a[j]有：

b[i,j]= 0 (i=0或j=0时)

b[i-1,j-1]+a[j] (i==j时)

max{ b[i,j-1]+a[j], (max b[i-1,t])+a[j] } (i<j时)，其中i≤t≤j-1

由于元素可相邻，故此问题可以看看成是子段和问题，也可以看成是子序列问题。

3、最大不相邻子段和（找出任意个不相邻子段使和最大）：设 b[j] 为 a[1,2,...,j] 不相邻子段和的最大值（不要求包括a[j]），则根据 b[j] 是否包括 a[j] 有：b[j]= max{ a[j]+b[j-2], b[j-1] }。相关：LeetCode198：House Robber

    public int maxNonadjacentSun(int[] nums) {
        if(nums.length==0)return 0;
        if(nums.length==1)return nums[0];
        
        int b1=0,b2=nums[0],tmp;
        for(int i=1;i<nums.length;i++)
        {
            tmp=b1+nums[i];
            b1=b2;
            if(b2<tmp)
            {
                b2=tmp;
            }
        }
        return b2;
    }

对于第一、第三种，由于b[j]只和前一个或两个状态有关，因此可以不设数组b[]而是采用数个变量来求；对于第二种同理可以只用两个数组来实现。

4、推广：

最小子段和

最大/最小连续子段积

设有序列 a[1,2,...,n]，设f(k)为a[1,2,...k]中包含a[k]元素的最大连续子数组积，相应的g(k)为包含a[k]的最小连续子数组积，

则 f(k) = max( f(k-1) * a[k], a[k], g(k-1) * a[k] ), g(k) = min( g(k-1) * a[k], a[k], f(k-1) * a[k] ) ，从而易在O(n)内求之。

2、和为给定值的种数

 设有序列 a[1,2,...,n]，给定数sum。

1、子段和的种数（和为sum的子段种数）

（1）有O(n)时间复杂度的算法，具体见后文的“前缀和问题”一节。 

（2）（非最优解）当各元素非负时可用动态规划：设dp[i,j]为从序列前i个数中选若干个数使得和为j的种数（要求选中的必须包含a[i]），有：

dp[i,j]= 

0，i=0时；

a[i]==j?1:0，i=1时；

a[i]==j?1:0 + dp[i-2, j] ，i>1且a[i]>j时；

( a[i]==j?1:0 + dp[i-2, j] ) + ( dp[i-1, j-a[i] ] )，i>1且a[i]≤j时 （根据dp[i,j]是否仅包含a[i]）

时间复杂度、空间复杂度均为O(n*sum) 。这显然不是好的方法，特别是sum很大时；此外，此法应用场景有限，要求各元素非负，写于此只是用于说明动态规划在此题的用法。

另外，上述的递推式实际上是适合于自底向上动态规划实现的递推式（其特点是i、j非负），相应地，我们可以写出适合于自顶向下动态规划实现的递推式（特点是i、j可负）：

dp(i, j)=

0, i<=0或j<0时;

( a[i]==j?1:0 + dp(i-2, j) ) + ( dp(i-1, j-a[i] ) )，其他

可见，这种形式更简洁，通过允许i、j负值使得几个分支合并到最后分支了。

2、子序列种数（和为sum的子序列的种数）

1、求序列中两数和等于sum的种数：LeetCode1：TwoSum

2、求序列中若干个数和等于sum的种数。

（1）最优解法是？

（2）当各元素非负时可用动态规划：设dp[i,j]为从序列前i个数中选若干个数使得和为j的种数，则：

dp[i,j]=

1，i=0且j=0时；

0, i=0且j>=0时；

dp[i-1,j]，a[i]>j时；

（ dp[ i-1,j-a[i] ] )+ ( dp[i-1,j] ), a[i]≤j时  （根据是否包含a[i]有两种情况）

    public static int resolve(int[] a, int sum) {// num of solutions that addup to sum
        if (a == null || a.length == 0) {
            return 0;
        }
        int n = a.length;
        int[][] dp = new int[n + 1][sum + 1];
        dp[0][0] = 1;
        // dp[i][k]=0,k>0，默认被初始化了
        for (int i = 1; i <= n; i++) {
            for (int j = 0; j <= sum; j++) {
                if (a[i - 1] > j) {
                    dp[i][j] = dp[i - 1][j];
                } else {
                    dp[i][j] = dp[i - 1][j] + dp[i - 1][j - a[i - 1]];
                }
                System.out.printf("(%d,%d):%d
", i, j, dp[i][j]);
            }
        }
        return dp[n][sum];
    }

时间复杂度、空间复杂度均为O(n*sum) 

3.2、字符串问题-子段

字符串的子段即子串。子串问题通常用动态规划或滑动窗口解决 

1、一个字符串的子串问题通常用滑动窗口方法解决。如：

最短覆盖子串：LeetCode-76。具体可参阅上面双指针部门内容。

最长不重复子串：LeetCode-3 

最长递增子串：

动态规划法：设dp[i]为a的前i个元素中以a[i]结尾的最长递增子串，则dp[i]= (a[i]≥a[i-1]) ? (dp[i-1]+1) : 1  ，base case：dp[1]=1。

时间复杂度O(n)，空间复杂度O(n)，由于当前状态只跟前一状态有关故可使用一个变量记录上一状态值从而使得空间复杂度降到O(1)

// 动态规划法
    public int resolveByDynamic(int[] nums) {
        int[] dp = new int[nums.length];

        int res = 0;

        // ==== 空间复杂度O(n) =====
        dp[0] = 1;
        for (int i = 1; i < nums.length; i++) {
            // 求dp[i]
            dp[i] = nums[i] >= nums[i - 1] ? dp[i - 1] + 1 : 1;
            // 更新结果
            if (res < dp[i]) {
                res = dp[i];
            }
        }
        // ==== 空间复杂度O(1) =====
        int curMaxlen = 1;// 对应上面dp[0]=1
        for (int i = 1; i < nums.length; i++) {
            curMaxlen = nums[i] >= nums[i - 1] ? curMaxlen + 1 : 1;
            if (res < curMaxlen) {
                res = curMaxlen;
            }
        }

        return res;
    }

滑动窗口法，与动态规划有点像：

O(n)、O(1)

    // 滑动窗口法
    public int resolveByWindow(int[] nums) {
        int resStart = 0, maxLen = 0;

        int s = 0, e = 0;

        while (e < nums.length) {
            // 右边界有效
            if (s == e || nums[e] >= nums[e - 1]) {
                // 更新窗口：do nothing

                // 更新结论
                if (maxLen < e - s + 1) {
                    resStart = s;
                    maxLen = e - s + 1;
                }
            } else {
                // 滑动左边界
                s = e;
            }
            e++;
        }

        return maxLen;// 若要返回该串则可借助resStart
    }

 

2、最长公共子串：

设 dp[i,j]  为序列a1[1,2,...,i ]、a2[1,2,...j ] 的包含未元素的最长公共子串的长度，则dp[i,j]= (a1[i]==a2[j])? (dp[i-1,j-1]+1): 0 }

    private static int resolve(String s1, String s2) {
        if (s1 == null || s2 == null) {
            return 0;
        }
        int n = s1.length();
        int m = s2.length();
        int max = 0;
        int[][] dp = new int[n + 1][m + 1];
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                dp[i][j] = (s1.charAt(i - 1) == s2.charAt(j - 1)) ? (dp[i - 1][j - 1] + 1) : 0;
                if (max < dp[i][j]) {
                    max = dp[i][j];
                }
            }
        }
        return max;
    }

3、最长回文子串：LeetCode-5

设dp[i,j]表示si,...,sj是否为回文子串，则dp[i,j]= dp[i+1,j-1] && (s[i]==s[j]), i≤j; 初始：dp[i,i]=true,dp[i,i+1]=s[i]==s[i+1]
O(n2),O(n2)

public class Solution {
    //最长回文子串和最长回文子序列不一样。。
    //设dp[i,j]表示si,...,sj是否为回文子串，则dp[i,j]= dp[i+1,j-1] && (s[i]==s[j]), i≤j; 初始：dp[i,i]=true,dp[i,i+1]=s[i]==s[i+1]
    //O(n2),O(n2)
    public String longestPalindrome(String s) {
        if(s==null || s.length()==0) return "";
        int len=s.length();
        
        boolean [][]dp=new boolean[len][len];//标记dp[i+1,j-1]即左下角是否为回文子串
        int resI=0,resJ=0;
        for(int i=len-1;i>=0;i--)
        {
            dp[i][i]=true;//dp[i,i]=true;
            for(int j=i+1;j<len;j++)
            {
                dp[i][j]= (j==i+1)?(s.charAt(i)==s.charAt(j)):(dp[i+1][j-1] && (s.charAt(i)==s.charAt(j)));
                if((dp[i][j]==true) && (resJ-resI+1 < j-i+1))
                {
                    resI=i;
                    resJ=j;
                }
            }
        }
        return s.substring(resI,resJ+1);
    }
}

  

3.3、字符串问题-子序列

子序列问题通常用动态规划解决。

1、最长递增子序列（LIS）：

动态规划：设dp[i]为a的前i个元素中以a[i]结尾的最长递增子序列，则dp[i]= max{ dp[j] } +1，其中j∈[1,i-1]且a[i]≥a[j]，，base case：dp[k]=1，k∈[1,n]。

O(n²)、O(n)

    public int lengthOfLIS(int[] nums) {
        int[] dp = new int[nums.length];

        int res = 0;
        for (int i = 0; i < nums.length; i++) {
            // 求dp[i]
            dp[i] = 1;// 初始为1
            for (int j = 0; j < i; j++) {
                if (nums[i] >= nums[j] && dp[i] < dp[j] + 1) {
                    dp[i] = dp[j] + 1;
                }
            }
            // 更新结果
            if (res < dp[i]) {
                res = dp[i];
            }
        }

        return res;
    }

也可将序列排序后求排序序列与原序列的最长公共子序列，时间复杂度也是O(n²)

有O(nlgn)的贪心算法——Patience Game：

过程：n张卡片分堆，依次确定每张放在哪堆中，决策依据：若当前卡片面值大于等于已有各堆堆顶的卡片面值则放新堆；否则找堆顶卡片面值大于当前卡片面值的最左边的堆。

证明：基于上述过程，一个堆中元素会严格递减，故每堆最多只可有一个卡片作为LIS的成员，从而LIS长度≤堆数；另一方面，从左往右各堆堆顶元素会递增，故等号可取到。

实现：由于各堆堆顶元素从左到右递增，故可用二分查找找最左堆，从而时间复杂度为O(n*lgn)，代码：

public int lengthOfLIS(int[] nums) {
    int[] top = new int[nums.length];
    // 牌堆数初始化为 0
    int piles = 0;
    for (int i = 0; i < nums.length; i++) {
        // 要处理的扑克牌
        int poker = nums[i];

        /***** 搜索左侧边界的二分查找 *****/
        int left = 0, right = piles;
        while (left < right) {
            int mid = (left + right) / 2;
            if (top[mid] > poker) {
                right = mid;
            } else if (top[mid] < poker) {
                left = mid + 1;
            } else {
                right = mid;
            }
        }
        /*********************************/
        
        // 没找到合适的牌堆，新建一堆
        if (left == piles) piles++;
        // 把这张牌放到牌堆顶
        top[left] = poker;
    }
    // 牌堆数就是 LIS 长度
    return piles;
}

拓展：

1、Patience Sorting——在上述game后重复移除最小的堆顶元素，移除的序列即为有序序列。"Patience sorting is the fastest wayto sort a pile of cards by hand."

2、二维形式——信封嵌套问题（LeetCode-354）：给定一批信封，每个有长宽两个属性，如 [[5,4],[6,4],[6,7],[2,3]] 。求能互相嵌套（能把小的放到大的里）的最多信封数。解法：把每个信封看做一维形式中的每个数即可，不同之处在于这里数间相对位置不是固定的而是可以移动，故先根据一个维度排序再用上述一维形式求解即可。可参阅：https://github.com/labuladong/fucking-algorithm/blob/master/算法思维系列/信封嵌套问题.md

代码：时间复杂度为 排序复杂度+一维LIS复杂度

class Solution {
    public int maxEnvelopes(int[][] envelopes) {
        Arrays.sort(envelopes, new Comparator<int[]>() {
            public int compare(int[] a, int[] b) {
               return a[0] == b[0] ? 
                    b[1] - a[1] : a[0] - b[0];
          }
        });
        return lengthOfLIS(envelopes);
    }
    public int lengthOfLIS(int[][] nums) {//O(n2)
        int[] dp = new int[nums.length];

        int res = 0;
        for (int i = 0; i < nums.length; i++) {
            // 求dp[i]
            dp[i] = 1;// 初始为1
            for (int j = 0; j < i; j++) {
                if (nums[i][0] > nums[j][0] && nums[i][1] > nums[j][1] && dp[i] < dp[j] + 1) {
                    dp[i] = dp[j] + 1;
                }
            }
            // 更新结果
            if (res < dp[i]) {
                res = dp[i];
            }
        }

        return res;
    }
}

 

2、最长公共子序列（LCS）：设 dp[i,j]  为序列a1[1,2,...,i ]、a2[1,2,...j ] 的最长公共子序列的长度，则dp[i,j]= (a1[i]==a2[j])? (dp[i-1,j-1]+1): max{ dp[i-1,j], dp[i,j-1] }

a与a的排序序列的LCS为a的LIS；a与a的反转序列的LCS为a的最长回文子序列

3、最长回文子序列：https://leetcode.com/problems/longest-palindromic-subsequence/#/description

法1：即求字符串S与逆串的最长公共子序列

    public int longestPalindromeSubseq1(String s) {
        if(s==null || s.length()==0) return 0;
        
        int len=s.length();
        int [][]c=new int[len+1][len+1];
        for(int i=0;i<c.length;i++)
        {
            c[0][i]=0;
            c[i][0]=0;
        }
        
        for(int i=1;i<=len;i++)
        {
            for(int j=1;j<=len;j++)
            {
                if(s.charAt(i-1)==s.charAt(len-j))
                {
                    c[i][j]=c[i-1][j-1]+1;
                }
                else
                {
                    c[i][j] = c[i-1][j]>c[i][j-1] ? c[i-1][j] : c[i][j-1];
                }
            }
        }
        return c[len][len];
    }

法2：动态规划

设dp[i,j]表示si,...sj的最长回文子序列的长度，其中i≤j，则dp[i,j]= 

dp[i+1,j-1]+2, si=sj时；

max{ dp[i,j-1], dp[i+1,j] }, si≠sj时

代码（可以仿照上面最长回文子串的实现方式）：

public int longestPalindromeSubseq(String s) {
        if(s==null || s.length()==0) return 0;
        
        int len=s.length();
        int [][]f=new int[len][len];
        
        for(int i=len-1;i>=0;i--)
        {
            f[i][i]=1;
            for(int j=i+1;j<len;j++)
            {
                if(s.charAt(i)==s.charAt(j)) f[i][j]=f[i+1][j-1]+2;
                else f[i][j]=Math.max(f[i+1][j],f[i][j-1]);
            }
        }
        return f[0][len-1];
    }

也可以啰嗦点实现：

设字符串为s，f(i,j)表示s[i..j]的最长回文子序列。 最长回文子序列长度为f(0, s.length()-1)
状态转移方程如下：
当i>j时，f(i,j)=0。
当i=j时，f(i,j)=1。
当i<j并且s[i]=s[j]时，f(i,j)=f(i+1,j-1)+2。
当i<j并且s[i]≠s[j]时，f(i,j)=max( f(i,j-1), f(i+1,j) )。
注：如果i+1=j并且s[i]=s[j]时，f(i,j)=f(i+1,j-1)+2=f(j,j-1)+2=2，这就是当i>j时f(i,j)=0的好处。

    public int longestPalindromeSubseq(String s) {
        if(s==null || s.length()==0) return 0;
        
        int len=s.length();
        int [][]f=new int[len][len];
        
        for(int i=len-1;i>=0;i--)//由于递推式每次最多后移一行，因此从最后一行起
        {
            // for(int j=0;j<len;j++)//由于递推式每次最多前移一列，因此从第一列起。但由于创建f时元素自动初始化为0，所以这里可以从i起
            for(int j=i;j<len;j++)
            {
                if(i>j) f[i][j]=0;
                else if(i==j) f[i][j]=1;
                else
                {//i<j
                    if(s.charAt(i)==s.charAt(j)) f[i][j]=f[i+1][j-1]+2;
                    else f[i][j]=Math.max(f[i+1][j],f[i][j-1]);
                }
            }
        }
        return f[0][len-1];
    }

 

4、前缀和问题

给定一个数组a[n]，求和为给定数字k的子数组（即元素要连续）的个数。

暴力法：两层循环以穷举每个子数组、再一层循环以求子数组和，然后判断是否等于k

时间复杂度O(n³)、空间复杂度O(1)

改进法1：借助前缀数和以去掉第三层循环，避免每次计算子数组和

时间复杂度O(n²)、空间复杂度O(n)：借助一个数组sum[n]计算到当前元素为止的元素累加和，则子数组a[i, ..., j]的和为sum[j]-sum[i-1]或sum[j]

时间复杂度O(n²)、空间复杂度O(1)：不借助求和数组，而是只借助一个变量来记住前缀数组和：

int subAryCount(int a[], int n, int k){
    int res=0;
    for(int i=0; i<n; i++){
        int sum=0;
        for(int j=i; j<n; j++){
            sum+=a[j];
            if(sum==k){ res++; }
        }
    }
    return res;
}

改进法2：利用前缀和以去掉第二层循环——在sum[]上做文章，两层循环以检查sum[j]-sum[i]为k的情况数，换个角度有sum[j]-k=sum[i]，因此可以用map记住截止到当前元素a[i]时前缀和sum[i]出现的次数，从而看a[i]-k出现的次数即可。这样只要一次扫描。

时间复杂度O(n)、空间复杂度O(n)，代码非常简洁

int subAryCount(int a[], int k){
    int res=0;

    Map<Integer, Integer> preSum2CntMap = new HashMap<>();
    preSum2CntMap.put(0,1);
    for(int i=0, preSum=0; i<a.length; i++){
        preSum+= a[i];
        res+= preSum2CntMap.getOrDefault(preSum-k, 0);
        preSum2CntMap.put(presum, preSum2CntMap.getOrDefault(preSum, 0)+1);
    }

    return res;
}

 子段和相关的问题可以考虑用前缀和，但是可能并不是最优的解法，如最大字段和用前缀和的效率并比动态规划差。

3、其他有趣的问题或小技巧

1、遍历某元素周围的元素：以统一而非手动穷举的方式遍历元素a[i][j]的上下左右元素：（借助方向数组）

// 方向数组 d 是上下左右搜索的常用手法
int[][] d = new int[][]{{-1,0}, {0,1}, {1,0}, {0,-1}};
for (int k = 0; k < 4; k++) {
    int x = i + d[k][0];
    int y = j + d[k][1];
    //(x, y)分别为(i, j)的四周的元素
}

2、String to Integer（atoi）：逐个字符处理，res=res*10+ ch-'0';，但是需要判断溢出，细节处理有点麻烦。可以换个思路判断：res> (Integer.MAX_VALUE-(ch-'0'))/10 时即溢出，这样可以省很多细节。

相关题目：https://leetcode.com/problems/string-to-integer-atoi/#/description

3、蛇形打印方阵：（打印对角行元素，只不过每次右上、左下方向依次交换）

#include <stdio.h>

#define M 100

void traverse(int a[][M],int n)
{//每次打印的数据个数为1、2、3、...、n、n-1、...、2、1，依次打印之，只不过右上方向和左下方向时坐标相应地增减下 
    int i=0,j=0;
    int count,loop;
    int dir=1;
    for(count=1;count<=n;count++)
    {
        if(dir==1)
        {//右上方向 
            for(loop=1;loop<count;loop++)
            {
                printf("%d ",a[i--][j++]);
            }
            printf("%d ",a[i][j]);
            if(j==n-1) i++;
            else j++;
        }
        else
        {//左下方向 
            for(loop=1;loop<count;loop++)
            {
                printf("%d ",a[i++][j--]);
            }
            printf("%d ",a[i][j]);
            if(i==n-1) j++;
            else i++;
        }
        dir=-dir;
    }
    
    for(count=n-1;count>0;count--)
    {
        if(dir==1)
        {
            for(loop=1;loop<count;loop++)
            {
                printf("%d ",a[i--][j++]);
            }
            printf("%d ",a[i][j]);
            if(j==n-1) i++;
            else j++;
        }
        else
        {
            for(loop=1;loop<count;loop++)
            {
                printf("%d ",a[i++][j--]);
            }
            printf("%d ",a[i][j]);
            if(i==n-1) j++;
            else i++;
        }
        dir=-dir;
    }
}

int main(int argc,char *argv[])
{
    int n=4;
    int a[n][M];
    for(int i=0;i<n;i++)
    {
        for(int j=0;j<n;j++)
        {
            a[i][j]=n*i+j+1;
        }
    }
    traverse(a,n);
}

4、n! 中0的个数：直接求n!的值再数0的个数显然数据一大几乎不可能求得。转换方向：由于0由2*5产生（就算是4*5等产生，最终也是由2*5产生），所以n! 中0的个数="2*5"的个数=5的个数（因为一个数的因子中2的个数肯定比5的个数多）

求n! 中5的个数：由于n!=1*2*...*n，（详情参阅：n的阶乘末尾0的个数）

法1：穷举法，求1~n中每个数的因子5的个数

int fun1(int n)
{
    int num = 0;
    int i,j;
    for (i = 5;i <= n;i += 5)
    {
        j = i;
        while (j % 5 == 0)
        {
            num++;
            j /= 5;
        }
    }
    return num;
}

法2：Z = N/5 + N /(5*5) + N/(5*5*5)，直到式子为0

int fun2(int n)
{
    int num = 0;
    
    while(n)
    {
        num += n / 5;
        n = n / 5;
    }
    
    return num;
}

5、给定n、m，求使得 i*j 为完全平方数的序列 (i,j) 的个数，其中 i ∈[1,n]、j ∈[1,m]：

    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int res = 0;
        int n = sc.nextInt();
        int m = sc.nextInt();
        // ssr(a,b)是整数 等价于sqrt(a*b)是整数 等价于a*b是完全平方数
        // 暴力O(n*m)在大数据时超时，以下为O(n*sqrt(m))的方法
        for (int i = 1; i <= n; i++) {
            // 找到能整除i的最大的完全平方数s
            int s = 1;
            for (int x = 2; x * x <= i; x++) {
                if (i % (x * x) == 0) {
                    s = x * x;
                }
            }
            int r = i / s;// n去掉s因子后的结果
            // 要使a*b是完全平方数，b需要因子r和一个完全平方数
            for (int y = 1; y * y * r <= m; y++) {
                res++;
            }
        }
        System.out.println(res);
        sc.close();
    }

6、给定一个由数字组成的字符串，求出其可能回复的所有IP地址。如"25525512110"对应的ip地址可以为[255,255,121,10, 255,255,12,110]

    private static void split(long sVal, int[] segments, int segmentId, List<String> ips) {// split(Long.parseLong(str), new int[4], 3, ipStrs);
        if (segmentId == 0) {
            if (0 <= sVal && sVal <= 255) {
                ips.add(sVal + "," + segments[1] + "," + segments[2] + "," + segments[3]);
            }
        } else {
            int mod, segmentVal;
            for (int exp = 1; exp <= 3; exp++) {
                mod = (int) Math.pow(10, exp);
                segmentVal = (int) (sVal % mod);
                if (0 <= segmentVal && segmentVal <= 255) {
                    segments[segmentId] = segmentVal;
                    split(sVal / mod, segments, segmentId - 1, ips);
                }
            }
        }
    }

7、给定一个随机生成器，生成0和1的概率分别为0.5，如何构造生成0和1的概率分别为0.3、0.7的随机生成器？

法：对0、1进行组合。

int MyFun()
{
  int n1=fun();
  int n2=fun();
  int n3=fun();
  int n4=fun();
  int n=n1;
  n|=n2<<1;
  n|=n3<<2;
  n|=n4<<3;
  if(n<=2) return 0;
  else if(n<10) return 1;
  else return MyFun();
}

随机生成器生成0和1的概率分别为p和1-p，如何构造等概率随机生成0和1的生成器？

法：由于生成01和10的概率均为p(1-p)，所以可以根据之实现：

int MyFun()
{
  int n1=fun();
  int n2=fun();
  int n=n1();
  n|=n2<<1;
  if(n==2) return 0;
  else if(n==1) return 1;
  else return MyFun();
}

8、一个递减序列循环左移若干位后，从其中查找一个数的O(lgn)方法：类似于折半查找

int find(int data[],int n,int v)
{
    int s=0,e=n-1,mid;
    while(s<=e)
    {
        mid=s+(e-s)/2;
        if(v==data[mid]) return mid;
        else if( (data[s]>=v && v>data[mid]) || (v<=data[s] && data[s]<data[mid]) ||(v>data[mid] && data[s]<data[mid]) )
        {//有三种情况使得落于左半子序列：左半子序列递减且v位于其间、左半子序列非递减且v位于非递减的前段如21765、左半子序列非递减且v位于非递减的后段如21765、
            e=mid-1;
        }
        else//落于右半子序列的情况类似 
        {
            s=mid+1;
        }
    }
    return -1;
}

9、大整数乘法（字符串整数乘法）

大整数通常超过了整型的表示范围，因此用字符串表示整数，如 "321" * "753"，求其同样用字符串表示的结果。LeetCode-43

思路：模拟竖式计算，设每个数下标从右到左且从0起，num1的每位数分别与num2的每位数相乘。用到的技巧：

num1[i]*num2[j]结果的个位刚好位于  [i+j]  位置上；

每位相乘不计算进位，而是最后统一处理进位。

代码：时间复杂度O(mn)、空间复杂度O(m+n)，m、n分别为两个串的长度

class Solution {//设每个数下标从右到左且从0起。模拟竖式计算：num1的每位数分别与num2的每位数相乘，num1[i]*num2[j]结果位于[i+j]中，每位相乘不计算进位，而是最后统一处理进位

    public String multiply(String num1, String num2) {

        int m=num1.length();
        int n=num2.length();
        int []tmpRes=new int[m+n];
    
        for(int i=0;i<m;i++){
            for(int j=0;j<n;j++){
                int mul=(num1.charAt(m-1-i)-'0') * (num2.charAt(n-1-j)-'0');
                tmpRes[i+j]+=mul;
            }   
        }

        //处理进位
        for(int i=0;i<m+n-1;i++){
            if(tmpRes[i]>9){
                tmpRes[i+1]+=tmpRes[i]/10;
                tmpRes[i]%=10;
            }
        }

        //去除前导0
        int i=m+n-1;
        while(i>0 && tmpRes[i]==0){
            i--;
        }
        //转为字符串
        StringBuffer sb=new StringBuffer();
        for(;i>=0 ; i--){
            sb.append((char)(tmpRes[i]+'0'));
        }
        return sb.toString();
    }

推荐参考资料

普林斯顿算法课-COS423